International Journal of Fluid Dynamics
Vol.05 No.02(2017), Article ID:20924,13
pages
10.12677/IJFD.2017.52007
A High Resolution Finite Volume Scheme for One Dimensional Euler Equations
Yixin Kang1, Taofeng Xie2, Wei Gao1
1School of Mathematical Sciences, Inner Mongolia University, Hohhot Inner Mongolia
2School of Computer and Information Science, Inner Mongolia Medical University, Hohhot Inner Mongolia

Received: May 23rd, 2017; accepted: Jun. 9th, 2017; published: Jun. 12th, 2017

ABSTRACT
In this paper, a high resolution finite volume scheme is proposed to solve one dimensional Euler equations. We use the Hermite interpolation method to construct the present scheme. Two kinds of convection boundedness criteria TVD and CBC are combined to suppress nonphysical wiggles of linear schemes near discontinuities. Some typical test cases show that the present numerical scheme can solve one dimensional Euler equation with discontinuous initial profiles efficiently.
Keywords:Euler Equations, Hermite Interpolation, High Resolution, CBC, TVD
一维Euler方程的高分辨率有限体积格式
康亦欣1,谢桃枫2,高巍1
1内蒙古大学数学科学学院,内蒙古 呼和浩特
2内蒙古医科大学计算机信息学院,内蒙古 呼和浩特
收稿日期:2017年5月23日;录用日期:2017年6月9日;发布日期:2017年6月12日

摘 要
本文提出一种高精度有限体积格式数值求解一维Euler方程。为克服线性高阶格式在解的间断附近产生非物理振荡,作者利用Hermite插值多项式,结合对流有界性准则TVD和CBC构造了本文的数值格式。典型算例验证表明,本数值格式可以很好的计算一维Euler方程的间断初值问题。
关键词 :Euler方程,Hermite插值,高阶格式,CBC,TVD

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
一维Euler方程是典型的非线性守恒律方程,依据守恒三大定律导出,是一种重要的计算流体力学模型方程,应用于气体动力学,流体力学及环境等学科领域,但该方程常常难于解析求解,需使用数值计算方法进行求解。
低阶精度的对流项数值格式,例如一阶迎风格式FOU (First-order Upwind),Lax-Friedrichs格式和Power-law格式,数值耗散太大。对流项的高阶精度格式HO (High-Order Scheme),如中心插风格式CD (Central Difference)、二阶迎风格式SOU(Second-order Upwind) [1] 、Lax-Wendroff [2] 、QUICK(Quadratics Upstream Interpolation for Convective Kinematics) [3] 和三阶迎风插值CUI(Cubic Upwind Interpolation) [4] 。然而,依据Godunov结论 [5] ,高阶精度格式不满足有界性,容易在间断解和大梯度处产生非物理震荡,导致数值不稳定性,破坏计算结果。
为解决这一难题,消除非物理震荡,研究者结合有界性准则,在高阶精度格式的基础上,进一步提出了高分辨率格式HR (High-Resolution Scheme) [6] [7] 。高分辨率格式可以更为有效地处理间断解处的问题,消除数值解的非物理震荡。Harten提出TVD (Total Variational Diminishing Constraint)准则 [6] ,也有文章提到Kolgan [8] 在Godunov-type里提出过一个类似TVD的概念来抑制非物理震荡 。为保证格式无震荡性,研究者们在此基础上也提出了其他限制器函数,例如Sweby的MINMOD [6] 、Roe的SUPERBEE [9] 以及van Leer的MUSCL [10] 等,这些限制器函数的提出推动了计算流体力学的迅速发展。此外,Gaskell和Lau提出CBC(Convection Boundness Criterion)条件来构造对流有界的数值格式,例如SMART [11] 、CLAM [12] 、STOIC [13] 、HOAB [14] 、WACEB [15] 、CUBISTA [16] 等格式都结合应用到了CBC条件,但,Yu et al. [18] , Hou et al. [19] 和Wei et al. [20] 表明CBC准则只能保证对流格式的有界性,因而Hou et al. [19] 和Wei et al. [20] 在CBC的基础上提出BAIR (Boundedness Accuracy and Interpolative Reasonableness)准则,来确保对流格式的二阶精度及有界性。在进行计算时,人们将高分辨率格式,高阶格式和CBC-BAIR条件正则化,使得计算观察更加方便。
本文根据高阶格式的特性,结合TVD准则和CBC-BAIR条件,在数值格式的正则变量形式的基础上,利用Hermite插值,得到一种高分辨率有限体积格式。文章首先对Euler方程和对流有界性则进行介绍并给出对流项高分辨率格式的构造过程;利用三阶精度TVD Runge-Kutta格式对时间项进行离散;通过一些经典的算例与问题对计算格式进行进一步的讨论,然后对一维守恒型的Euler方程的Lax激波管问题和Shu-Osher问题进行计算,验证新构造格式的有效性;最后总结全文得出结论。
2. 方法
2.1. Euler方程
在一维理想气动方程组的守恒形式中,Euler方程是一个典型的非线性守恒系统,它依据质量守恒、动量守恒和能量守恒三大定律推导得出。
Euler方程可以写成:
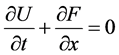 (1)
(1)
式中 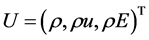
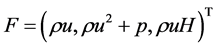
在守恒形式的Euler方程中,称流动密度、速度及压力变量为原始变量,密度、动量、总能为守恒变量;
其中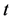 为时间,
为时间, 为从坐标原点出发的距离,
为从坐标原点出发的距离, 为流动密度,
为流动密度,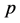 为压力,
为压力,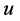 为质点速度,
为质点速度, 为单位
为单位
体积流体总能,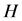 为总焓。状态方程
为总焓。状态方程 ,其中
,其中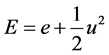 ,
,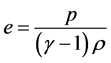 为内能;
为内能;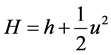 ,
, 为焓,
为焓, 为比热容比,完全气体时,
为比热容比,完全气体时, ,把方程写成拟线性形式时,Jacobi
,把方程写成拟线性形式时,Jacobi
矩阵为
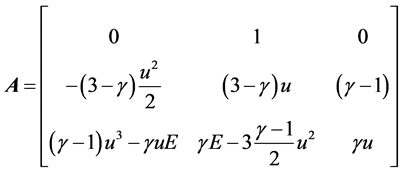
矩阵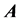 的特征值为
的特征值为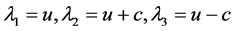 ,其中
,其中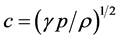 表示当地声速。由于方程组的特征值是三个互异实数,所以方程组是双曲型的。
表示当地声速。由于方程组的特征值是三个互异实数,所以方程组是双曲型的。
因为Euler方程是研究计算流体力学计算方法的主要模型,而所谓Riemann问题就是求解Euler方程,
在初值

下的解,此类初值问题初始时一般不满足间断关系。随着时间的变化,初始间断处分解成一些特定的流动结构,但是远离这些结构的地方流动仍保持初始值。Riemann问题解的情况可能是两侧为均匀流区和中部为间断影响区,所以需要构造格式既满足高阶精度,又能有效的处理间断解处的问题,消除数值解的非物理震荡。
2.2. 对流有界性准则
图1中U,C,D和f是相邻的三个网格节点及控制单元界面。U,C,D分别表示上游点(upwind),中游点(central),下游点(downwind)。表1中的线性高阶格式界面值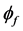 ,通过相邻的三个网格节点
,通过相邻的三个网格节点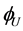 ,
,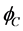 和
和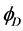 对其进行重构,得到表达式如下:
对其进行重构,得到表达式如下:
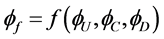 (2)
(2)
为便于高阶格式的研究,根据Leonard [17] 正则化定义,对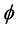 正则化得到
正则化得到
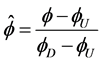 (3)
(3)

Figure 1. Three neighboring mesh points and the mesh face
图1. 三个相邻结点及单位边界
Table 1. The linear convection schemes and the normalized variable formations
表1. 线性对流格式及其正则化形式
联立上述方程,我们可以得到
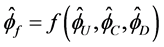 (4)
(4)
显然可知 ,
,  ,将上述公式化简为
,将上述公式化简为
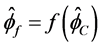 (5)
(5)
因此可以看出界面值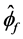 只与
只与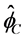 有关。
有关。
高阶格式通过对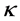 格式赋值得到,
格式赋值得到, 格式公式化后如下:
格式公式化后如下:
 (6)
(6)
正则化后得到公式
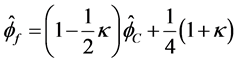 (7)
(7)
其中 的值只依赖于
的值只依赖于 ,其中
,其中 的参数变化范围为
的参数变化范围为 。表1中对
。表1中对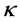 赋于不同的值可以得到不同的正则化高阶格式,从表中可以看出所有格式至少都为二阶精度。由Godunovs定理 [5] 可知,格式在间断解处仍然会产生非物理振荡,所以需要结合线性高阶精度格式和有界性准则来构造高分辨率格式(HR),有效的抑制非物理振荡。
赋于不同的值可以得到不同的正则化高阶格式,从表中可以看出所有格式至少都为二阶精度。由Godunovs定理 [5] 可知,格式在间断解处仍然会产生非物理振荡,所以需要结合线性高阶精度格式和有界性准则来构造高分辨率格式(HR),有效的抑制非物理振荡。
根据Gaskell和Lau [11] 提出的CBC准则。构造在NVF (Normalized Variable Formations)形式下的CBC格式,表达式为
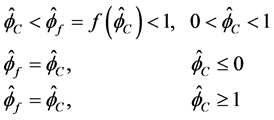 (8)
(8)
NVF形式下的BAIR准则可以表达为
 (9)
(9)
此外,Harten提出的TVD (总变差不增)准则 [6] ,可以保证数值解是物理解,无振荡性,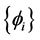 表示总
表示总
变差值,且满足
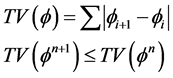 (10)
(10)
TVD准则被Swbey [7] 转化为限制函数:
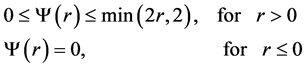
其中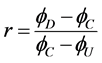 ,在NVF形式下可以表示为
,在NVF形式下可以表示为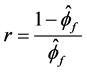 。
。
由上述公式,我们可以得到NVF格式下的TVD限制器函数的表达式:
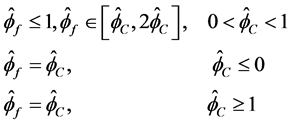
图2是CBC-BAIR条件和TVD约束准则。
2.3. 格式构造
正则化的高分辨率格式可以表示成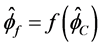 ,根据Zijlema和Wesseling的结论 [21]
,根据Zijlema和Wesseling的结论 [21]
1) 高分辨率格式的NVD线必须落在位于TVD和CBC-BAIR的区域内;
2) NVD线在NV坐标内必须通过点 ,且至少满足二阶精度差;
,且至少满足二阶精度差;
3) NVD线在NV坐标内满足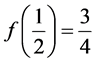 及
及 ,同时与
,同时与 格式具有相同的精度。
格式具有相同的精度。
由以上结论推得,高分辨率格式NVD线必过 ,
, 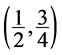 ,
, 这三个点,选取这三个插值节点的函数值,以及CUI线性格式下的对应的导数值
这三个点,选取这三个插值节点的函数值,以及CUI线性格式下的对应的导数值 ,
,  ,
,  ,构造插值多项式。
,构造插值多项式。
由给定三个互异节点及节点的导数值,得到五次插值函数。

Figure 2. The regions of the TVD (shaded) and BAIR (hatched)
图2. TVD条件和BAIR条件
新构造的高阶格式(HRFVM):
 (11)
(11)
特征线如图3所示,从图中可以看出HRFVM格式严格满足TVD准则和CBC-BAIR条件。
2.4. 时间项离散
空间离散后,对时间项进行离散。设半离散化方程为:
 (12)
(12)
为保证时间上的高阶精度,采用三阶精度的TVD型Runge-Kutta方法对时间项进行离散, 其中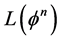 是空间离散算子,
是空间离散算子,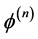 为第
为第 时间层的守恒量。
时间层的守恒量。
格式如下
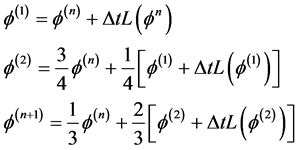 (13)
(13)
3. 数值算例
3.1. 线性对流方程
 (14)
(14)
以下通过两个不同的初值条件验证数值格式的精度及准确性。
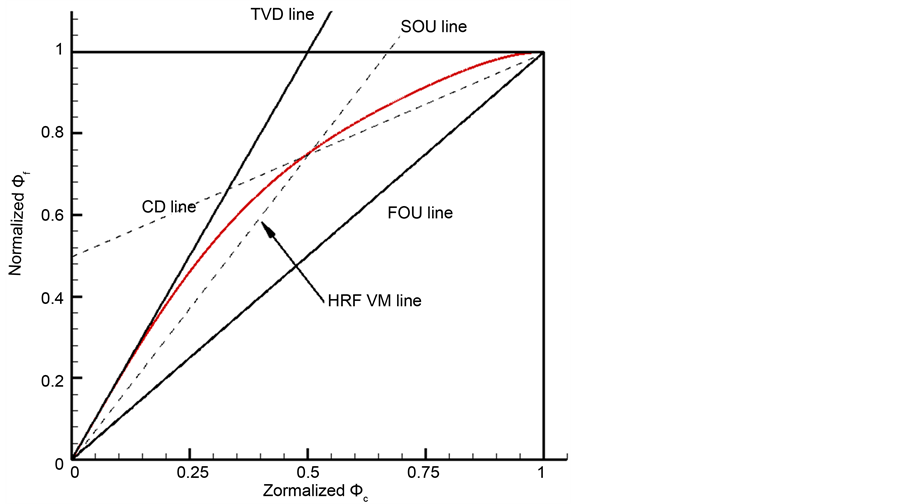
Figure 3. The NV line of the HRFVM scheme in the BAIR and TVD region
图3. HRFVM曲线与BAIR和TVD区域
3.1.1. 精确解算例
对于一阶线性对流方程,给定初值条件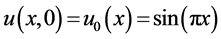 ,线性对流速度
,线性对流速度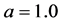 ,计算求解区域为
,计算求解区域为 ,
, 数为0.1,周期
数为0.1,周期 。如表2将新构造的高分辨率格式HRFVM与SMART和HOAB两格式进行比较,分别计算网格数在20,40,80,160和320下,
。如表2将新构造的高分辨率格式HRFVM与SMART和HOAB两格式进行比较,分别计算网格数在20,40,80,160和320下, 的误差及精度阶。
的误差及精度阶。
给出格式精度阶的计算公式
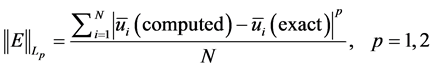 (15)
(15)
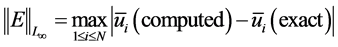 (16)
(16)
 (17)
(17)
可以从表2中看出,三种格式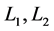 的误差随着网格剖分不断加密而减小,且新格式的精度阶与SMART和HOAB一样,它的
的误差随着网格剖分不断加密而减小,且新格式的精度阶与SMART和HOAB一样,它的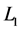 的精度阶已经达到二阶。
的精度阶已经达到二阶。
3.1.2. 间断解算例
非光滑复合初始条件
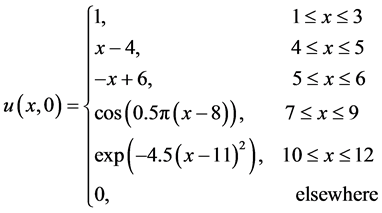
该数值算例的求解区域是 ,
, 数为0.25,计算到时间
数为0.25,计算到时间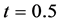 ,网格数2500,网格距
,网格数2500,网格距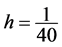 ,
,
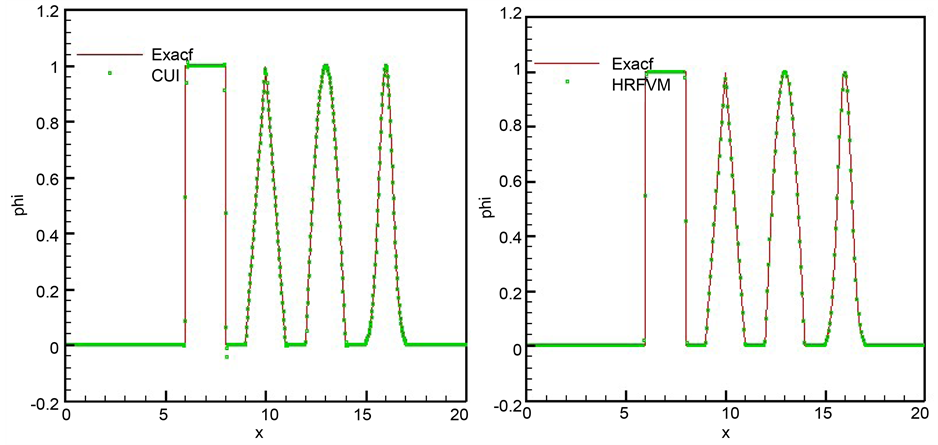
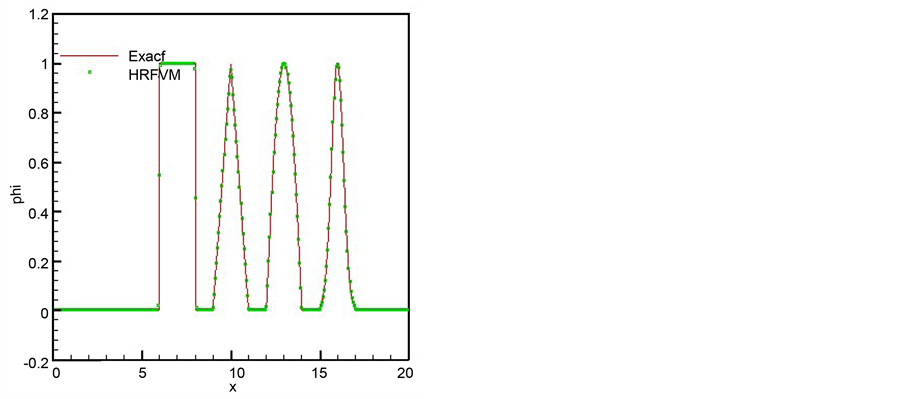
下图4我们将CUI (a), HRFVM (b)格式的数值解与准确解作比较。CUI格式在光滑求解区域内精确解与数值解的逼近效果良好,但在网格剖分如此密的情况下,间断解处仍然有一定的耗散,而新格式数值计算结果与精确解的逼近程度良好。
 (a) (b)
(a) (b)
Figure 4. Comparison of numerical and exact results for the linear equations with nonsmooth initial distribution (a) CUI; (b) HRFVM
图4. 比较非光滑复合初始条件下线性对流方程的准确解和数值解(a) CUI;(b) HRFVM
Table 2. Errors and orders for several selected schemes
表2. 格式误差与数值精度阶对比
3.2. 非线性方程
3.2.1.一维无粘性Burgers方程
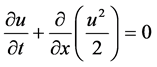 (18)
(18)
初值条件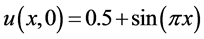 及周期性边界条件
及周期性边界条件 。
。
其中 。在
。在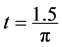 时,将HRFVM格式的数值解与非线性Burgers方程的精确解进
时,将HRFVM格式的数值解与非线性Burgers方程的精确解进
行比较,求解区域 剖分网格单元数为400,
剖分网格单元数为400,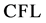 取0.5。
取0.5。
图5中看出,各时刻下数值解与准确解都吻合的特别好,HRFVM格式未产生非物理震荡。
3.2.2. Buckely-Leverett问题
非凸通量函数Buckely-Leverett方程如下
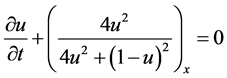 (19)
(19)
初值条件

Figure 5. Comparison of the numerical and exact solutions with one-dimen- sional inviscid Burgers equations
图5. 比较一维无粘Burgers方程数值解与准确解
时间步长 ,取
,取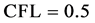 ,计算求解区域
,计算求解区域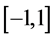 的网格数为200,计算终止时间
的网格数为200,计算终止时间 ,通过图6对格式数值计算结果与精确解的比较,可看出格式能够有效的捕捉间断和激波,具有高分辨率和低数值耗散性。通过与GAMMA格式的比较,说明HRFVM格式能够很好的模拟准确解。
,通过图6对格式数值计算结果与精确解的比较,可看出格式能够有效的捕捉间断和激波,具有高分辨率和低数值耗散性。通过与GAMMA格式的比较,说明HRFVM格式能够很好的模拟准确解。
3.3. Euler方程
3.3.1. Lax激波管问题
Lax激波管问题,取黎曼初始条件
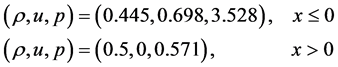
求解计算区域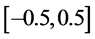 网格剖分为320份,计算到
网格剖分为320份,计算到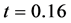 。应用构造的新格式HRFVM来计算密度、速度、压强和总能量。如图7所示,同WENO5格式(该格式既适用于间断解,又能处理复杂连续流场)进行比较,新格式的数值计算结果都很好的逼近WENO5。
。应用构造的新格式HRFVM来计算密度、速度、压强和总能量。如图7所示,同WENO5格式(该格式既适用于间断解,又能处理复杂连续流场)进行比较,新格式的数值计算结果都很好的逼近WENO5。
3.3.2. Shu-Osher 问题
Shu-Osher问题是一个典型的激波熵波相互作用的问题,激波同正弦波之间相互干扰,引发高频率振动,因而解的剖面图中既包含光滑解又包含波动解。
初始条件
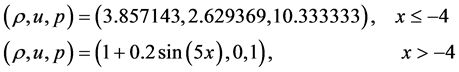
分别取两种网格节点N = 1000和N = 2000进行比较,求解计算区间 ,计算终止时间
,计算终止时间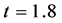 。同样以WENO5为参考值,对密度进行比较,可以从图8看出当网格更加细化时计算结果收敛于参考值。
。同样以WENO5为参考值,对密度进行比较,可以从图8看出当网格更加细化时计算结果收敛于参考值。
4. 总结
本文在TVD准则和CBC-BAIR条件下利用Hermite插值构高分辨率有限体积格式。通过求解一维
 (a) (b)
(a) (b)
Figure 6. The Buckley-Leverett equation (a) HRFVM and (b) GAMMA
图6. 比较HRFVM格式与GAMMA格式在数值解与准确解
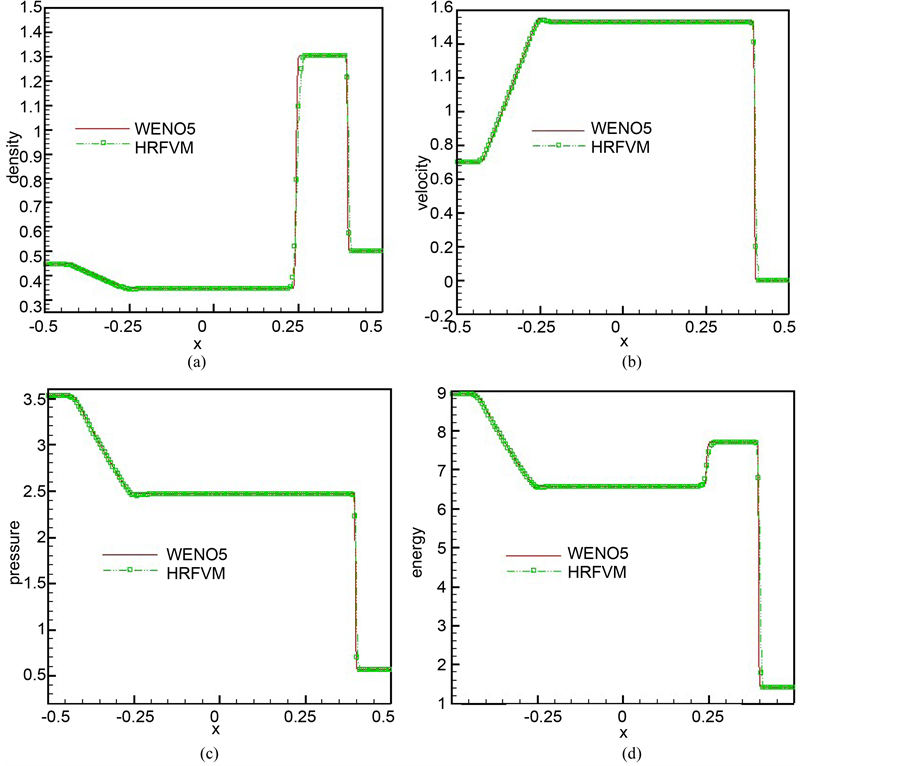
Figure 7. The Lax problem of one-dimensional Euler equation: the computed solutions with the reference solutions: (a) Density; (b) Velocity; (c) Pressure; (d) Energy
图7. 一维Euler方程Lax问题计算(a)密度;(b)速度s;(c)压力;(d)总能量
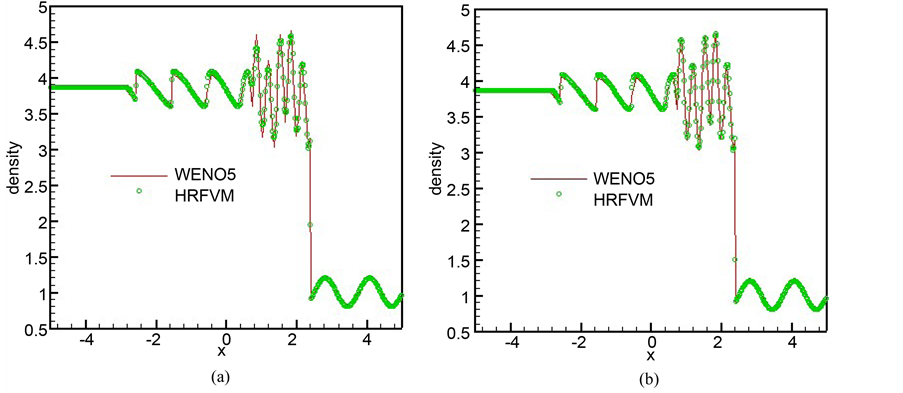
Figure 8. The Shu-Osher problem with (a) 1000 cells and (b) 2000 cells
图8. Shu-Osher问题网格数(a) 1000; (b) 2000
Euler方程的Lax问题和Shu-Osher问题,数值结果表明本文的数值格式能够有效地消除非物理振荡,并保持良好的间断逼近效果。
致谢
作者感谢审稿专家给予本文宝贵的修改意见和建议以及期刊编辑对于本文的付出。
基金项目
本文由内蒙古自治区人才开发基金项目(12000-1300020240)和内蒙古自然科学基金项目(2015MS0101)支持。
文章引用
康亦欣,谢桃枫,高 巍. 一维Euler方程的高分辨率有限体积格式
A High Resolution Finite Volume Scheme forOne Dimensional Euler Equations[J]. 流体动力学, 2017, 05(02): 56-68. http://dx.doi.org/10.12677/IJFD.2017.52007
参考文献 (References)
- 1. Shyy, W. (1985) A Study of Finite Difference Approximations to Steady-State, a Convection-Dominated Flow Problem. Journal of Computational Physics, 57, 415-438. https://doi.org/10.1016/0021-9991(85)90188-3
- 2. Lax, P.D. and Wendroff, B. (1960) Systems of Conservations Laws. Communications on Pure and Applied Mathematics, 13, 217-237. https://doi.org/10.1002/cpa.3160130205
- 3. Leonard, B.P. (1979) A Stable and Accurate Modeling Procedure Based on Quadratic Interpolation. Computer Methods in Applied Mechanics and Engineering, 19, 59-98. https://doi.org/10.1016/0045-7825(79)90034-3
- 4. Agarwal, R.K. (1981) A Third-Order-Accurate Upwind Scheme for Navier-Stokes Solutions at High Reynolds Numbers. AIAA Paper 1981-112 in 19th AIAA Aerospace Sciences Meeting, St. Louis, 12-15. https://doi.org/10.2514/6.1981-112
- 5. Roe, P.L. (1986) Characteristic-Based Schemes for the Euler Equations. Annual Review of Fluid Mechanics, 18, 337- 365. https://doi.org/10.1146/annurev.fl.18.010186.002005
- 6. Harten, A. (1983) High Resolution Schemes for Hyperbolic Conservation Laws. Journal of Computational Physics, 49, 4357-4393. https://doi.org/10.1016/0021-9991(83)90136-5
- 7. Sweby, P.K. (1984) High Resolution Schemes Using Flux Limiters for Hyperbolic Conservation Laws. SIAM Journal on Numerical Analysis, 21, 995-1011. https://doi.org/10.1137/0721062
- 8. Kolgan, V.P. (2011) Application of the Minimum-Derivative Principle in the Construction of Finite-Difference Schemes for Numerical Analysis of Discontinuous Solutions in Gas Dynamics. Journal of Computational Physics, 230, 2384-2390. https://doi.org/10.1016/j.jcp.2010.12.033
- 9. Roe, P.L. (1986) Characteristic-Based Schemes for Euler Equations. Annual Review of Fluid Mechanics, 18, 365-377. https://doi.org/10.1146/annurev.fl.18.010186.002005
- 10. Van Leer, B. (2005) Towards the Ultimate Conservative Difference Scheme. Monotonicity and Conservation Combined in a Second-Order Scheme. Journal of Computational Physics, 202, 196-215.
- 11. Gaskell, P.H. and Lau, A.K.C. (1988) Curvature-Compensated Convective Transport: SMART, A New Boundedness- Perserving Transport Algorithm. International Journal for Numerical Methods Fluids, 8, 617-641. https://doi.org/10.1002/fld.1650080602
- 12. Zhu, J. (1991) A Low-Diffusive and Oscillation-Free Convective Scheme. Journal of Applied Mechanical Engineering, 7, 225-232.
- 13. Darwish, M.S. (1993) A New High-Resolution Scheme Based on the Normalized Variable Formulation. Numerical Heat Transfer, Part B, 24, 337-353. https://doi.org/10.1080/10407799308955898
- 14. Wei, J.J., Yu, B. and Tao, W.Q. (2003) A New High-Order-Accurate and Bounded Scheme for Incompressible Flow. Numerical Heat Transfer, Part B, 43, 19-41. https://doi.org/10.1080/713836153
- 15. Song, B., Liu, G.R., Lam, K.Y. and Amano, R.S. (2000) On a Higher-Order Discretization Scheme. International Jour- nal for Numerical Methods in Fluids, 32, 881-897. https://doi.org/10.1002/(SICI)1097-0363(20000415)32:7<881::AID-FLD2>3.0.CO;2-6
- 16. Alves, M.A., Oliverira, P.J., and Pinho, F.T. (2003) A Convergent and Universally Bounded Interpolation Scheme for the Treatment of Advection. International Journal for Numerical Methods in Fluids, 41, 47-75. https://doi.org/10.1002/fld.428
- 17. Leonard, B.P. (1988) Simple High-Accuracy Resolution Program for Convective Modeling Discontinuities. International Journal for Numerical Methods in Fluids, 8, 1291-1318. https://doi.org/10.1002/fld.1650081013
- 18. Yu, B., Tao, W.O., Zhang, D.S. and Wang, Q.W. (2001) Discussion on Stability and Boundedness of Convective Discretized Scheme. Numerical Heat Transfer, Part B, 40, 343-365. https://doi.org/10.1080/104077901317091721
- 19. Hou, P.L., Tao, W.Q. and Yu, M.Z. (2003) Refinement of the Convective Boundedness Criterion of Gaskell and Lau .Engineering. Computation, 20, 1023-1043. https://doi.org/10.1108/02644400310503008
- 20. Wei, J.J., Yu, B., Taobao, W.Q., et al. (2003) A New High-Order-Accurate and Bounded Scheme for Incompressible Flow. Numerical Heat Transfer, Part B, 43, 19-41. https://doi.org/10.1080/713836153
- 21. Zijema, M. and Wesseling, P. (1995) Higher Order Flux-Limiting Methods for Steady-State, Multidimensional, Convection-Dominated Flow. Report 1995-131, Delft University of Technology, Delft.
