International Journal of Fluid Dynamics
Vol.06 No.02(2018), Article ID:25475,13
pages
10.12677/IJFD.2018.62005
Recovery-Based Error Estimator for the Natural-Convection Problem Based on Defect-Correction Method
Lulu Li, Haiyan Su
College of Mathematics and System Sciences, Xinjiang University, Urumqi Xinjiang
Email: lulisay123@sina.com, shymath@163.com
Received: May 28th, 2018; accepted: Jun. 12th, 2018; published: Jun. 19th, 2018

ABSTRACT
This article solves an artificial viscosity stabilized nonlinear problem in the defect step, and corrects the residual by linearized equations in the correction step for a few steps. In both the defect and correction steps, we use the Oseen iterative scheme to solve the discrete nonlinear equations, considering the stress tensor
. For the speed and pressure of NC problem, we use the lowest finite element pair
. The discrete finite element stress tensor approximation
is discontinuous piecewise constant. We obtain the local recovery type error estimator
by the convergence recovery technique to construct
in continuous space. Finally, the stability, accuracy and efficiency of the proposed method are confirmed by several numerical investigations.
Keywords:Natural-Convection Problem, Defect Correction Method, Gradient Recovery, Posterior Error Estimates, Error Analysis
基于亏量校正求解自然对流问题的 后验误差估计子
李露露,苏海燕
新疆大学,新疆 乌鲁木齐
Email: lulisay123@sina.com, shymath@163.com
收稿日期:2018年5月28日;录用日期:2018年6月12日;发布日期:2018年6月19日

摘 要
本文给出NC方程基于亏量校正方法的恢复型误差估计子。我们在亏量步求解人工黏性系数的稳定非线性问题;在校正步通过线性化方程来校正这个残量,在亏量和校正步我们都采用Oceen迭代。考虑应力张量
,若我们采用最低阶协调速度和压力有限元对
求解离散NC问题,应力张量的有限元逼近
是不连续的分片常数。我们利用超收敛片恢复技巧构造连续空间的量
,得到了局部恢复型误差估计子
。最后,通过数值实验验证了基于亏量校正方法的恢复型误差估计子是有效的。
关键词 :Natural-Convection方程,亏量校正方法,梯度恢复,后验误差估计子,误差估计

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
Natural convection (NC)自然对流问题,即浮力驱动流体运动,在实际问题中经常出现。定常NC问题是粘性流体不可压缩流动和传热过程的耦合方程,其中不可压缩流体是Boussinesq’s近似,在大气动力学中,它是一个重要的强迫耗散非线性系统,它不仅包含速度矢量场和压力场,而且包含温度场,从热力学角度讲,我们知道,流体的运动粘度会产生一定的热量,因此,流体的运动必须伴随着温度的相互转换,速度和压力。因此,对这一非线性系统的研究具有重要意义。对于自然对流方程的数值分析和数值结果,Christie和Mitchell [1] ,Boland和Layton [2] 等人进行了很多研究。此外,Ҫɪbɪk和Kaya [3] 提出了基于投影的稳定化有限元方法求解稳态自然对流问题。
我们提出一种基于亏量校正方法后验恢复的误差估计方法来解决NC问题。亏量校正方法的主要思想是:我们在亏量步求解人工黏性系数的稳定非线性问题;在校正步通过线性化方程来校正这个残量,在亏量和校正步我们都采用Oceen迭代。众所周知,缺陷校正方法是求解非线性稳态问题的一种迭代改进技术。该方法在不需要网格的情况下,提高了解的精度,对对流占优问题有效。它被用来解决Layton等人的Navier-Stokes方程 [4] 。作为一个非线性问题,NC方程的近似误差由两部分组成:一个是由有限元离散化产生的,另一个是由非线性方程迭代产生的。由Oceen迭代方案缺陷校正技术相结合,提出了一种新的算法。在亏量及校正的步骤中,我们利用Oceen方案求解离散方程,这种新方法继承了每个算法的最佳特征,它是无条件稳定的。
本文中,我们采用最低阶协调速度和压力有限元对
离散NC问题。应力张量
的有限元逼近
是不连续的分片常数。我们利用超收敛片恢复技巧 [5] 构造连续空间的量
,得到了局部恢复型误差估计子
。这样计算出的近似解是比一般有限元方法求解的近似解更加逼近真解。所以,我们结合亏量校正方法和恢复型误差估计子求解稳定的NC方程,不仅能有效地解决对流占有问题,还能得到更加精确的近似解。
本文主要分为4个部分,首先介绍NC方程的主要性质和经典结果。第二部分提出亏量校正方法,并对其稳定性和误差估计进行简单分析。第三部分,结合恢复型误差估计子求解NC方程。最后数值实验验证了我们方法的有效性和可靠性。
2. 预备知识
2.1. 定常NC方程
假设Ω是一个有界、凸开区域,其边界
是Lipschitz连续的,令
,其中
是
的正则开子集。我们考虑下面的NC方程:
(2.1)
这里
是流体速度,
是流体压力,
是温度,
是外力方程,
是Prandtl数和Rayleigh数,
是热传导系数,
是一个二维向量,n是
的外法线。
接下来,介绍一些Hilbert空间:
,
。
中定义L2-标量内积
和L2-范数
。我们在空间X和W中同样定义内积
和范数
。标准定义是在Sobolev空间
中,其范数为
,
。我们将
和其范数
写作和
。此外,定义
的对偶空间为
,对偶空间中的范数定义为
,且
是X的对偶空间。
方便起见,我们假设u,v属于同一个有限元空间X。下面分别定义两个连续双线性形式
和
和一个三线性形式
:
(2.2)
(2.3)
此外,我们需要在定义两个双线性形式
和一个三线性形式
在
和
中,有
根据上面定义的双线性形式和三线性形式,有以下两个已知结论( [6] [7] [8] ):
(2.4)
(2.5)
其中
是两个只依赖于
的定常数。
现在给出一个定义在
上的广义双线性形式:
它满足连续性和
条件:
其中,
是常数。它是与网格尺寸无关的,但是依赖于X和本文中的其他参数,
依赖于
和v。
NC方程(2.1)的变分形式如下:求解
对于任意的
,
(2.6)
下面给出原方程的解的存在唯一性的经典结论:
存在至少一个解对
满足(2.6)且
(2.7)
此外,若
满足下面的唯一性条件:
(2.8)
则
是方程(2.6)的唯一解。
2.2. 亏量校正方法
首先,我们给出有限元空间
,
其中
表示T上的分片线性多项式,
表示T的分片常数多项式。
我们给出
正交投影的定义:
显然有限元空间对
是不满足离散的
条件的,但是满足下面的性质A。
存在映射
,
和
满足
(2.9)
根据上述定义给出原方程的离散形式:求解
满足
(2.10)
由于我们选取的是
为不稳定元,所以考虑下面的罚跳跃稳定化方法:
其中
为
的单元内边的集合,
为q在边e上的跳跃,
为给定的稳定参数。
(2.11)
这里的
。
接下来,我们将介绍亏量校正方法 [9] ,它包括:在亏量步求解人工粘性稳定非线性问题,然后用线性化方程校正几个步骤的亏量解。在亏量及校正的步骤,我们使用最稳定的Oseen迭代求解离散方程。
新方法描述如下:
考虑下面稳定问题:求解
,对任意的
有
(2.12)
其中
是一个稳定的人工粘性系数。我们定义它的迭代解
,对任意的
满足
(2.13)
这里的
。
离散方程的亏量
定义为
(2.14)
根据下列方程求解校正量
(2.15)
这样,离散方程的亏量校正方法可以描述如下:
步骤1:求解稳定有限元迭代解
,对
有
(2.16)
其中
。
步骤2:求解校正解
满足
(2.17)
其中
。
流程图如下:
2.3. 稳定性和误差估计
我们给出上述方法的主要稳定性和误差估计结果。
定理2.1:假设
是方程(2.17)的解,满足:
根据(2.4)式和(2.5)式,(2.8)式和(2.13)式可以很容易得到定理2.1的证明。
定理2.2:假设
分别是方程(2.6)与(2.17)的解,C为正常数,则有下面估计:
证明:令
。用(2.6)减去(2.17)且
得
和
化简得
根据Young不等式可以得到
3. 基于亏量校正方法的恢复型误差估计子
3.1. 恢复型误差估计子
本小节中,我们将构造出一个恢复型误差估计子并分析它的性质。假设
数值结果,我们考虑应力张量
,和它的有限元近似
。
其中I是
的单位矩阵。Zienkienwicz-Zhu估计子的主要思想是将间断有限元梯度进行恢复得到一个连续的恢复项G (参考 [10] [11] )。
在
中分别定义
和
为:在
中所有顶点的集合,在
中的在
内部所有顶点的集合,v (
)的基函数共享一个顶点v的所有单元的集合
。
结合文献 [11] 中的超收敛片恢复技巧将分片常数张量
恢复到连续的从而获得一个恢复应力张量
。
对任意顶点
和它的片
,定义
其中
是三角剖分T的面积。细节可以参考文献 [12] 。
构造一个恢复型误差估计子。定义局部误差和全局误差:
恢复型误差估计子
有以下几个重要性质。证明方式与文献( [12] [13] )相似,不再赘述。
引理3.1:根据上述
和
的定义,存在两个与网格无关的常数
和
有
引理3.2:根据上述
和
的定义,存在一个与网格无关的常数C,可以得到以下
和
误差估计
.
3.2. 可靠性和有效性分析
定理3.1:假设
和
分别是(2.6)和(2.17)的解,存在一个与网格无关的正常数C有
证明:存在一个强制算子
有
因此,根据引理3.1,引理3.2,用Cauchy-Schwarz不等式,有
根据
的定义,近似解
满足
。
同时满足
。所以,结合引理,可得一下估计
定理3.1得证。
从引理3.1,可得
。
为了证明恢复型误差估计子
的有效性,首先需要估计:
和
引理3.3:假设
和
分别是(2.6)和(2.17)的解。存在一个与网格无关的正常数C有
证明:从
的定义出发,可得
下面定义插分算子
。用迹不等式有
定理3.2:假设
和
分别是(2.6)和(2.17)的解,存在一个与网格无关的常数C有
证明:结合上面的估计,用引理3.1和引理3.2,可得
完成了有效性的证明。
4. 数值实验
在本小节中,结合自适应方法给出两个个数值算例来验证我们所提方法的有效性。对于处理非线性部分,我们均采用Ocien迭代。
为了方便起见,下面给出几个定义:
(i)
表是三角剖
的自由度个数,
(ii)
(iii)
(iv) #Math_205#
4.1. 光滑解问题
第一个算例我们求解
区域上的一个光滑真解问题,从而验证我们的方法,对于光滑真解是有效的。我们给出真解
,压力p和温度T如下:
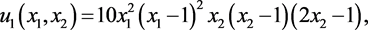
从表1中可以看出,基于亏量校正方法的后验误差估计是适用的。
趋于1表示我们的估计子与真实误差是有效渐进的,说明我们的方法是有效的。图1中(a)是初始网格,(b)是自适应加密后的网格,从图中可以看出,加密是有效的。
4.2. 方腔流
第二个数值实验我们考虑没有真解的方腔流问题。定义计算区域
。取
,
,
,边界定义如下:左边界和底部取
,底边取
,其余取
,且速度上

Table 1. The result of smooth solution with Pr = 0.71, κ = 1, Ra = 1000
表1. 光滑解结果,其中Pr = 0.71,κ = 1,Ra = 1000
 (a) (b)
(a) (b)
Figure 1. From left to right: original meth, refined meth
图1. 从左到右分别是初始网格和网格加密结果
 (a) (b)
(a) (b)
Figure 2. From left to right: original meth, refined meth
图2. 从左到右分别是初始网格和网格加密结果
 (a) (b) (c)
(a) (b) (c)
Figure 3. The numerical streamlines with Ra = 10, Ra = 1000, Ra = 1e5
图3. 数值结果的速度流线图:Ra = 10,Ra = 1000,Ra = 1e5
 (a) (b) (c)
(a) (b) (c)
Figure 4. The numerical isobars with Ra = 10, Ra = 1000, Ra = 1e5
图4. 数值结果的等压图:Ra = 10,Ra = 1000,Ra = 1e5
为0的Dirichlet条件。图1表示了自适应方法的初始网格和自适应后的网格。
图2表示初始网格和自适应加密后的网格,表示自适应方法在捕捉大误差处是有效的,加密结果是我们想要的。图3,图4分别表示不同Rayleigh数10,103,105的速度流线图和等温图。容易看出,我们的方法在求解没有真解的方腔流问题同样有效,其次在求解大Rayleigh方面比一般有限元更加有效。
5. 结论与展望
本文提出了基于亏量校正方法的恢复型误差估计子,通过数值实验,验证了我们方法的有效性和可靠性。同时,在求解方腔流大Rayleigh数问题时,由于在亏量步添加了人工黏性系数,使我们避免了对流占优情况的发生,而后的校正步与后验误差估计子使近似解更加地逼近真解,这样得出的结果是优于一般有限元方法的。此方法可以推广到其他流体的问题。
基金项目
不可压缩磁流体动力学方程的非协调自适应有限元高效算法研究(11701493)。
文章引用
李露露,苏海燕. 基于亏量校正求解自然对流问题的后验误差估计子
Recovery-Based Error Estimator for the Natural-Convection Problem Based on Defect-Correction Method[J]. 流体动力学, 2018, 06(02): 33-45. https://doi.org/10.12677/IJFD.2018.62005
参考文献
- 1. Christie, I. and Mithchell, R. (2010) Upwinding of High Order Galerkin Method in Conduction-Convection Problem. International Journal for Numerical Methods in Engineering, 12, 1764-1771. https://doi.org/10.1002/nme.1620121113
- 2. Boland, J.L.W. (1990) An Analysis of the Finite Element Method for Natural Convection Problems. Numerical Methods for Partial Dif-ferential Equations, 6, 115-126. https://doi.org/10.1002/num.1690060202
- 3. Ҫɪbɪk, K. and Kaya, S. (2011) A Projection Based Stabilized Finite Element Method for Natural Convection Problem. Journal of Mathematical Analysis and Applications, 381, 469-484. https://doi.org/10.1016/j.jmaa.2011.02.020
- 4. Layton, W., Lee, K. and Peterson, J. (2002) A Defect-Correction Method for the Incompressible Navier-Stokes Equations. Applied Mathematics and Computation, 129, 1-19. https://doi.org/10.1016/S0096-3003(01)00026-1
- 5. Ainsworth, M. and Oden, J. (1997) A Posteriori Error Estimation in Finite Element Analysis. Computer Methods in Applied Mechanics and Engineering, 142, 1-88. https://doi.org/10.1016/S0045-7825(96)01107-3
- 6. Layton, W. and Tobiska, L. (1998) A Two-Level Method with Back-tracking for the Navier-Stokes Equations. SIAM Journal on Numerical Analysis, 35, 2035-2054. https://doi.org/10.1137/S003614299630230X
- 7. Luo, Z. (2006) Theory Bases and Applications of Finite Element Mixed Methods. Science Press, Beijing.
- 8. Brézis, H. and Gallouet, T. (1980) Nonlinear Schrödinger Evolution Equations. Nonlinear Analysis: Theory, Methods and Applications, 4, 677-681. https://doi.org/10.1016/0362-546X(80)90068-1
- 9. Stetter, J. (1978) The Defect Correction Principle and Discretization Methods. Numerische Mathematik, 29, 425-443. https://doi.org/10.1007/BF01432879
- 10. Zienkiewicz, C. and Zhu, Z. (1992) The Superconvergent Patch Recovery and a Posteriori Error Estimates. Part 1: The Recovery Technique. International Journal for Numerical Methods in Engineering, 33, 1331-1364. https://doi.org/10.1002/nme.1620330702
- 11. Carstensen, C. (2004) Some Remarks on the History and Future of Averaging Techniques in a Posteriori Finite Element Error Analysis. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift fur Angewandte Mathematik und Mechanik, 84, 3-21. https://doi.org/10.1002/zamm.200410101
- 12. Song, L., Hou, Y. and Cai, Z. (2014) Recovery-Based Error Estimator for Stabilized Finite Element Methods for the Stokes Equation. Computer Methods in Applied Mechanics and Engineering, 272, 1-16. https://doi.org/10.1016/j.cma.2014.01.004
- 13. Song, L., Su, H. and Feng, X. (2016) Recovery-Based Error Estimator for Stabilized Finite Element Method for the Stationary Navier-Stokes Problem. SIAM Journal on Scientific Computing, 38, A3758-A3772. https://doi.org/10.1137/15M1015261





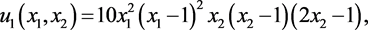
 (a) (b)
(a) (b) (a) (b)
(a) (b) (a) (b) (c)
(a) (b) (c) (a) (b) (c)
(a) (b) (c)