Open Journal of Acoustics and Vibration
Vol.04 No.03(2016), Article ID:19106,9
pages
10.12677/OJAV.2016.43005
Application of Equivalent Stiffness in Vertical Vibration Frequency of Car Body
Meng Zhang1, Shuoshao Zhang2, Hairong Sun2
1Liaoning Equipment Manufacturing Vocational and Technical College, Shenyang Liaoning
2CRRC Tangshan Co., Ltd., Tangshan Hebei
Received: Nov. 9th, 2016; accepted: Nov. 27th, 2016; published: Nov. 30th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The railway vehicle car-body can be equivalent to the uniform beam with a method of equivalent stiffness. Equivalent inertia moment Ie can be calculated with bending strain energy equality theory and a related coefficient according to car-body structure. With the Timoshenko beam theory and some models, a final formula is obtained. A simple car-body model and a high-speed car-body model are calculated with above method, and there are acceptable errors between analytical and finite element results, which is a reference method for car-body design.
Keywords:Equivalent Stiffness, Car Body, Timoshenko, Vibration Frequency

等效刚度法在车体垂向振动频率计算中 的应用研究
张萌1,张硕韶2,孙海荣2
1辽宁装备制造职业技术学院,辽宁 沈阳
2中车唐山机车车辆有限公司,河北 唐山
收稿日期:2016年11月9日;录用日期:2016年11月27日;发布日期:2016年11月30日

摘 要
本文采用等效刚度法,将铁道车辆车体这种复杂结构等效为等截面梁;应用弯曲变形能相等的原理,结合车体特征,并引入了相关修正系数,得到了车体的等效惯性矩Ie。以铁木辛柯梁的振动频率计算公式为依据,并在长度方向上对车体的面积及剪切形状系数进行了修正,得到了最终的计算公式。将简单车体及某型高速车体的参数代入公式,并将计算得到的结果与有限元结果进行了对比,证明了计算方法的可靠性,为车体垂弯频率的计算提供一种参考计算方法。
关键词 :等效刚度,车体,铁木辛柯,振动频率

1. 引言
长久以来,铁道车辆车体的刚度问题一直是车体设计工作中的关键,且相关标准 [1] [2] 中也对车体的刚度提出了相关要求。若车体刚度过大,表示车体过重,不符合节能环保要求,就需要进行轻量化设计;若刚度不足,将导致车体振动与转向架自振频率接近而产生共振,降低乘坐舒适度,影响车辆疲劳寿命 [3] ,存在引发重大安全事故的隐患。
机车车辆领域对车体刚度评价的一项重要指标为车体的一阶垂向弯曲振动频率,而目前获得列车车体一阶垂向振动弯曲频率主要通过有限元分析或者实车模态试验 [4] [5] [6] [7] [8] 。文献 [9] 以CRH3型动车组车体为研究对象,借助有限元软件对车体进行了振动模态的分析,并对局部结构的尺寸及强度进行了优化,使得优化后的结果能更好的满足使用条件。文献 [10] 对某型车体做了有限元分析及振动实验,并对两结果进行了对比,表明设备弹性连接的车体振动频率高于刚性连接。文献 [11] 在铁木辛柯梁理论的基础上,根据车体的特征对公式进行了修正,获得的解析结果与有限元结果十分接近,提供了一种铁道车辆车体一阶垂向弯曲振动频率解析计算参考方法。
本文采用一种等效刚度法,将车体等效为一种等截面梁,提供了另外一种车体一阶垂向振动频率计算的参考方法。
2. 计算原理
在众多工程实际应用中,往往会涉及到变截面梁变形及振动的问题,与等截面梁计算问题不同的是,变截面梁的计算并没有一种标准方法,虽然许多学者提出了多种不同的变截面梁变形计算方法,但适用条件多样,运算也非常复杂。这里采用一种等效刚度法,将车体这种复杂形式的变截面梁等效为等截面梁,达到了简化计算的目的,使得对于车体这种复杂结构的整体计算成为可能。
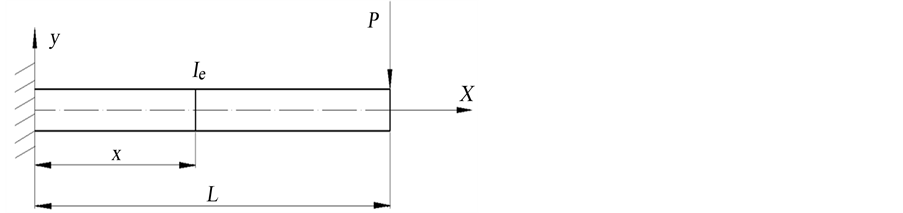
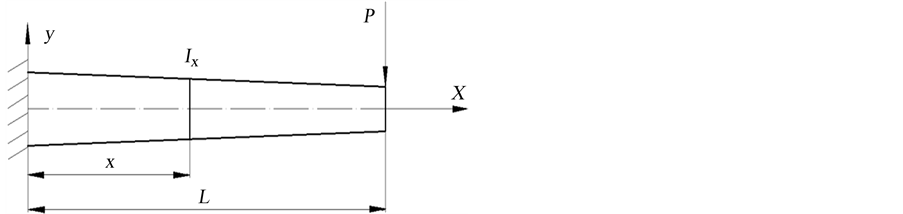
图1(a)表示变截面梁,其任一截面的惯性矩为Ix,图1(b)表示等截面梁,其任一位置的惯性矩为Ie。为将变截面梁等效为等截面梁,以两梁弯曲应变能相等的原理 [12] ,建立等式:
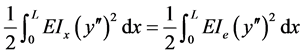 (1)
(1)
式中,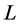 为梁长度,
为梁长度,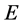 为梁的弹性模量,
为梁的弹性模量,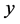 为挠曲线方程。
为挠曲线方程。
应用等效刚度法,必须先选择一个合适的挠曲线方程:
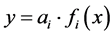 (2)
(2)
式中,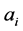 为位移参数,可根据精度要求选取,一般选取一个或两个位移参数可满足计算数度要求;
为位移参数,可根据精度要求选取,一般选取一个或两个位移参数可满足计算数度要求;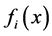 是满足几何边界条件的已知函数,通常选用三角函数或多项式函数。挠曲线方程的选取按图2所示支撑方式从表1中选取。
是满足几何边界条件的已知函数,通常选用三角函数或多项式函数。挠曲线方程的选取按图2所示支撑方式从表1中选取。
3. 事例计算
参照真实车体的整体参数,建立拥有4个门3个窗简单车体进行计算,简单车体三维模型如图3所示,其基本参数如表2所示。
为便于计算,将车体按照不同的截面进行粗分段,再以各段长度的最大公约数对各段进行细分,这样就可以将整个车体进行平均分段,分别计算各段的弯曲变形能求和,即可得到整车的弯曲变形能。示例车体粗分段示意图如图4所示。
分段生成如图5所示4种车体截面,各截面的基本参数如表3所示。
由于计算整车的的弯曲应变能,因此假设车体为图2(a)所示的简支梁,支点在车体两端,挠曲线方程选择表1中(a) ①,位移参数选择一项,即:
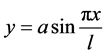 (3)
(3)
 (a) (b)
(a) (b)
Figure 1. Different type of sections
图1. 不同形式截面梁
 (a)
(a)
 (b)
(b)
 (c)
(c) (d)
(d)
Figure 2. Beams of different support methods
图2. 不同支撑方法的梁
Table 1. Deflection curve equation
表1. 挠曲线方程
Table 2. Basic parameters of simple car body
表2. 简单车体基本参数
Table 3. Simplified car body parameter
表3. 简化车体模型截面参数

Figure 3. Simple vehicle model
图3. 简单车体模型
由于车体存在门窗等功能性开孔,导致车体局部刚度变弱,因此在车体开门窗的位置引入门/窗系数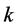 对式(1)的抗弯刚度EIx进行修正:
对式(1)的抗弯刚度EIx进行修正:
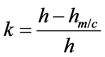 (4)
(4)
式中,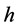 为车体高度,
为车体高度,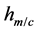 在车门位置取车门高度,在车窗位置取车窗高度。整车的总弯曲应变能U1:
在车门位置取车门高度,在车窗位置取车窗高度。整车的总弯曲应变能U1:
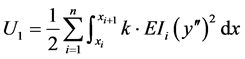 (5)
(5)

Figure 4. Schematic diagram: simply segmentation of car body
图4. 车体粗分段示意图
 (1) (2)
(1) (2) (3) (4)
(3) (4)
Figure 5. Different sections of car body
图5. 车体不同截面
式中,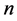 为车体分段数,
为车体分段数,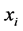 为第i段车体左端坐标值,
为第i段车体左端坐标值,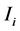 为第i段车体截面等效惯性矩,由于不同截面的形心并不在同一高度,因此应用平行移轴公式移动到车体质心所在位置。平行移轴公式 [13] 为:
为第i段车体截面等效惯性矩,由于不同截面的形心并不在同一高度,因此应用平行移轴公式移动到车体质心所在位置。平行移轴公式 [13] 为:
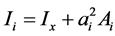 (6)
(6)
式中,Ix为截面对形心的惯性矩,ai为截面形心与车体质心垂向距离,Ai为截面面积。
等效简支梁的弯曲应变能U2:
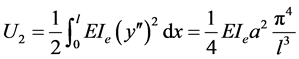 (7)
(7)
将解析算法以Matlab形成计算程序,计算得等效惯性矩: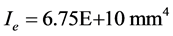
自由梁的铁木辛柯一阶垂向弯曲振动频率方程 [13] :
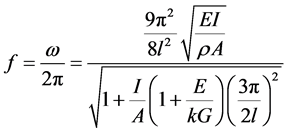 (8)
(8)
式中,l为车体长度,I将代入上述得到等效惯性矩Ie,E弹性模量,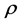 材料密度,A为车体等效面积,k为车体等效截面剪切形状系数,由于各个截面面积及剪切形状系数并不唯一,因此,将面积及剪切形状系数按长度进行等效:
材料密度,A为车体等效面积,k为车体等效截面剪切形状系数,由于各个截面面积及剪切形状系数并不唯一,因此,将面积及剪切形状系数按长度进行等效:
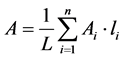 (9)
(9)
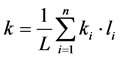 (10)
(10)
式中,L为车体长度,n为车体平均分段数,Ai为第i段的截面面积,li为第i段的长度,ki为第i段的剪切形状系数。由于车体在门窗处刚度较弱,且破坏了整体的剪切力流,因此,这种等效方式忽略了门窗的影响,使得整体刚度偏大,因此引入修正系数0.9对式(8)分子的抗弯刚度EI进行修正。将车体参数代入修正的铁木辛柯一阶垂弯振动频率方程,得其一阶垂弯频率为20.08 Hz,该车体的有限元结果为21.51 Hz (如图6所示),误差为1.43 Hz。
4. 实车验证
为验证该方法在真实车体计算中的效果,以某型高速车辆车体为原型,去除局部特征,得到计算车体的三维模型如图7所示,有限元计算结果如图8,其粗分段形式如图9所示。
分段共生成如图10所示的8种截面。
各个截面的基本参数如表4所示。
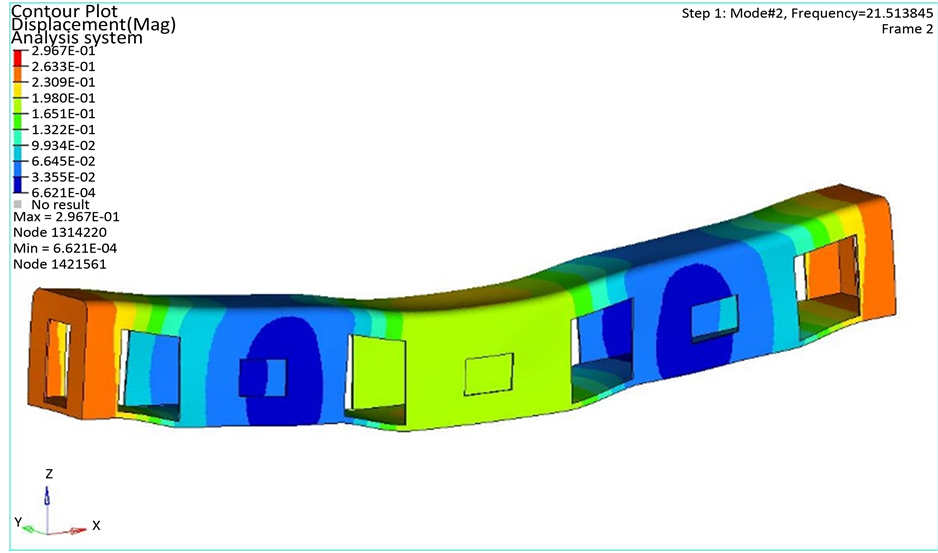
Figure 6. Finite element results of car body
图6. 车体有限元结果

Figure 7. High speed car model
图7. 高速车模型
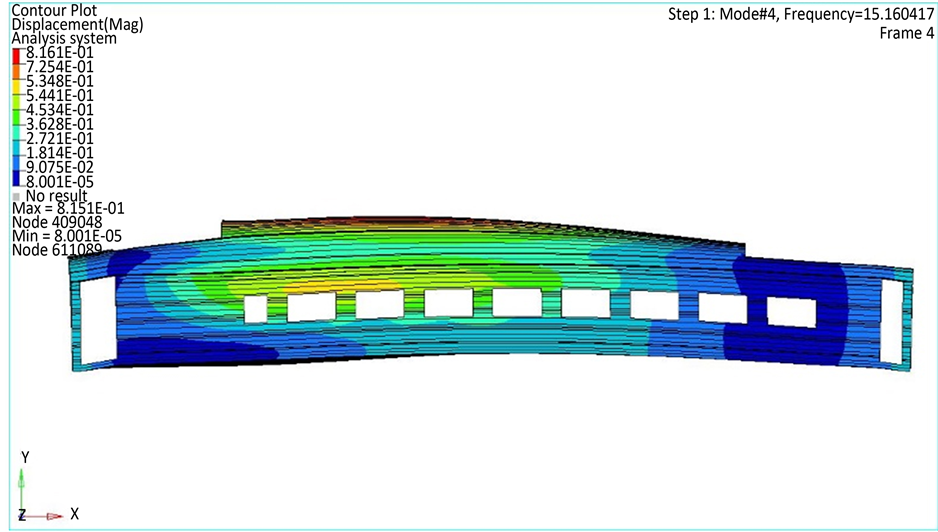
Figure 8. Finite element results of high speed car
图8. 高速车有限元结果
Figure 9. Schematic diagram: simply segmentation of high speed car
图9. 高速车粗分段示意图
 (a) (b)
(a) (b)
 (c) (d)
(c) (d)
 (e) (f)
(e) (f) (g) (h)
(g) (h)
Figure 10. Sections of high speed car
图10. 高速车截面
Table 4. Real car body parameter
表4. 实际车体模型截面参数
将车体数据进行等效后计算,得车体的一阶垂弯频率为16 Hz,车体的有限元结果为15.2 Hz,误差为0.2 Hz,进一步说明了该计算方法的有效性。
5. 结论
1) 将等效刚度法引入到车体这种复杂结构的计算当中,将变截面梁等效为等截面梁,简化了计算。
2) 引入了相关系数,对车体刚度进行了修正,增加了车体刚度对侧墙门窗等功能性开孔的敏感性。
3) 解析结果与有限元结果进行了对比,误差在工程要求范围内,验证了该解析方法的有效性,为车体设计工作提供了计算参考方法。
文章引用
张 萌,张硕韶,孙海荣. 等效刚度法在车体垂向振动频率计算中的应用研究
Application of Equivalent Stiffness in Vertical Vibration Frequency of Car Body[J]. 声学与振动, 2016, 04(03): 34-42. http://dx.doi.org/10.12677/OJAV.2016.43005
参考文献 (References)
- 1. TB/T1335-1996, 铁道车辆强度设计及试验鉴定规范[s].
- 2. EN12663:2010, Railway Applications—Structural Requirements of Railway Vehicle Bodies[s].
- 3. 于金朋, 张卫华, 孙帮成, 黄雪飞, 张立民, 肖守讷. 高速车体结构参数对车体模态频率的影响分析[J]. 铁道学报, 2015, 37(9): 32-37.
- 4. 吴会超, 邬平波, 吴娜, 等. 车下设备悬挂参数与车体结构之间的匹配关系研究[J]. 振动与冲击, 2013, 32(3): 124-128.
- 5. 张志华. 动车组铝合金车体结构强度分析[D]: [硕士学位论文]. 北京: 北京交通大学, 2007.
- 6. 白彦超, 胡震, 黄烈威. 出口加纳动车组动车车体强度有限元分析及结构优化[J]. 铁道车辆, 2009, 47(12): 17-21.
- 7. 沈彩瑜, 米彩盈. 重载电力机车车体强度和刚度研究[J]. 计算机仿真, 2014, 31(2): 230-234.
- 8. 王贺鹏. 车体自振频率的研究[D]: [硕士学位论文]. 大连: 大连交通大学, 2005.
- 9. 蓝剑红. CRH3型动车组车体刚度有限元分析[D]: [硕士学位论文]. 成都: 西南交通大学, 2012.
- 10. 张远亮, 张立民, 张艳斌, 孙现亮. 车体配重对车体1阶垂弯频率的影响分析[J]. 铁道机车车辆, 2015, 35(1): 51-53.
- 11. 阳光武, 高一丁, 万波. 车体一阶垂向振动弯曲频率解析分析[J]. 铁道车辆, 2015, 53(1): 1-5.
- 12. 邹家兴. 用等效刚度法计算变截面梁的变形[J]. 中国农村水利水电, 1995(9): 36-38.
- 13. 单辉祖. 材料力学[M]. 北京: 高等教育出版社, 2000.
