Geomatics Science and Technology
Vol.04 No.02(2016), Article ID:17460,7
pages
10.12677/GST.2016.42007
Concept of Arcangle of Curves and Its Applications
Bin Li
School of Mechanical Engineering, Southeast University, Nanjing Jiangsu

Received: Apr. 9th, 2016; accepted: Apr. 26th, 2016; published: Apr. 29th, 2016
Copyright © 2016 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Corresponding to arclength of curves, the concept of arcangle of curves in E3 is proposed. Arcangle of curves can be used as the index of evaluating the total curvature of wirelike objects; especially it can induce the concept of angular distance traveled of paths, which shows its potential application value.
Keywords:Curve, Curvature, Total Curvature, Arcangle, Angular Distance Traveled, Application

曲线的弧角概念及其应用
李彬
东南大学机械工程学院,江苏 南京

收稿日期:2016年4月9日;录用日期:2016年4月26日;发布日期:2016年4月29日

摘 要
与曲线的弧长对应,提出了E3中曲线的弧角概念。弧角可以作为三维线状物体或对象总弯曲程度的评价指标,特别是由其可以导出道路的角度路程概念,显示了其潜在的应用价值。
关键词 :曲线,曲率,全曲率,弧角,角度路程,应用

1. 引言
给定一段曲线,如何从整体上评价它,或者说,给出哪些描述其整体特性的度量指标是一个有意义的问题。显然,最常用的指标是弧长,它是曲线展直后的总长度。数学上,弧长是曲线弯曲和扭曲下的不变量,应用中则可以表示诸如质点的曲线运动路程、弯曲公路的路程,以及漆包线中铜线的卷绕长度等,因此,是一个重要的概念。然而,弧长不能反映曲线的形状,因此还需要其它的度量指标。这些指标也已经存在,如反映曲线总弯曲的全曲率和反映曲线总扭曲的全挠率等与曲线曲率和挠率有关的指标 [1] [2] 。然而,这里有两个问题。第一,例如,全曲率这个名称可能不利于应用。我们知道,所谓曲线的曲率是其切矢对于弧长的旋转速度,是一个角速度的概念,而全曲率为曲率对于弧长的积分,结果是角度而不是角速度(两者量纲不同),但全曲率字面上容易被理解成仍然是一种曲率(角速度)。第二,例如,虽然全曲率的数学意义(特别是闭合曲线)得到了充分的发掘 [1] [3] ,但其应用(特别是非闭合曲线和工程应用)似乎没有得到充分的关注。
注意到,圆弧的全曲率等于其圆心角,也就是圆弧对于其圆心所张成的角度。圆心角在一些文献中被称为弧角(arcangle) [4] - [6] ,恰好与圆弧的弧长对应。显然,这个名称直观,便于应用。那么,可否将这个概念推广到一般曲线上?本文就这个问题进行了讨论。
2. 定义
定义1:弧角
设C为E3中有限弧长简单正则曲线,称
 (1)
(1)
为C的弧角,其中,k(s)为C的曲率,s为C的自然参数。
显然,所定义弧角就是曲线的全曲率 [1] 。
说明:
①如图1所示,作曲线C上任一点P (在其密切平面Πo上)的密切圆(半径为1/k),则在忽略三阶以上小量的前提下,C与该密切圆在P点邻近一个微分弧长ds的范围内重合(C与该密切圆在P点至少二阶接触) [7] 。换言之,ds可视为一段微分圆弧,则其所对应的微分弧角dθ = kds。显然,取dθ的总和作为曲线的弧角定义是合理的。
②这一弧角概念反映的是曲线切矢方向变化的总角度,或者曲线弯曲的总角度。
③全挠率不可以作类似的定义,这是因为挠率的作用在于改变微分圆弧ds所在平面(密切平面)的方向,不影响其所对应的圆心角(微分弧角)。
定义2:测地弧角
设C为E3中简单正则曲面S上的有限弧长简单正则曲线,称
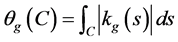 (2)
(2)
为C在S上的测地弧角,其中,kg(s)为C的测地曲率,s为C的自然参数。
显然,所定义测地弧角就是绝对测地全曲率。
说明:
①如图2所示,C为曲面S上的曲线,Cg为C在其上任一点P的切平面Πg上的(正)投影曲线。作Cg在P点的密切圆(C的测地密切圆,半径为1/kg),则在忽略三阶以上小量的前提下,Cg与该密切圆在P点邻近一个微分弧长dsg = ds的范围内重合。换言之,dsg可视为一段微分(测地)圆弧,则其所对应的微分(测地)弧角dθg = kgdsg = kgds。显然,取dθg绝对值的总和作为曲线的测地弧角定义是合理的。
②这一测地弧角概念反映的也是曲线切矢方向变化的总角度,但基准是按Levi-Civita矢量平行定义 [7] 所确定的方向。
③根据测地曲率的定义,可以得到 [7]
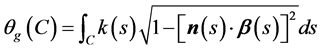 (3)
(3)
其中,k(s)为C的曲率,β(s)为C的主法矢,n(s)为S的法矢。

Figure 1. Osculating circle (red line), differential arc and differential arcangle
图1. 密切圆(红线所示)、微分圆弧与微分弧角
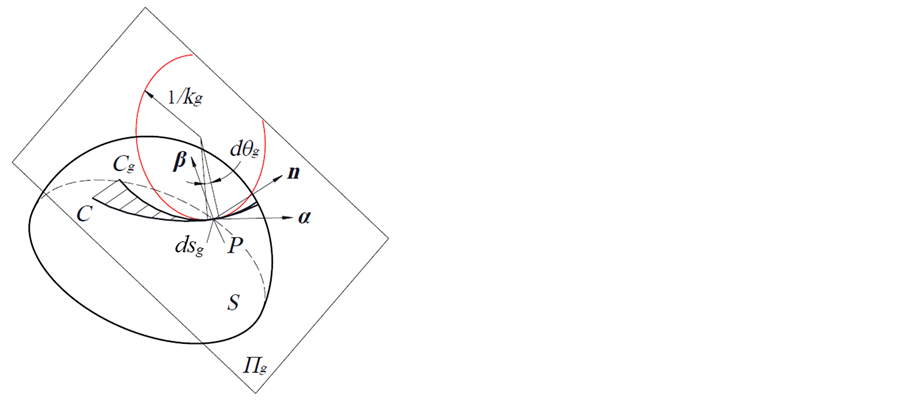
Figure 2. Geodesic osculating circle (red line), dif- ferential geodesic arc and differential geodesic arc- angle
图2. 测地密切圆(红线所示)、微分测地圆弧与微分测地弧角
定义3:投影弧角
设C为E3中(简单正则曲面S上的)有限弧长简单正则曲线,Ch为C在平面Πh上的(正)投影曲线,其中C上任一点的切矢都不垂直于平面Πh,称
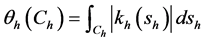 (4)
(4)
为C在平面Πh上的投影弧角,其中,kh(sh)为Ch的曲率,sh为Ch的自然参数。
说明:
①如图3所示,作Ch上任一点Ph的密切圆(C的投影密切圆,半径为1/kh),则在忽略三阶以上小量的前提下,Ch与该密切圆在Ph点邻近一个微分弧长dsh的范围内重合。换言之,dsh可视为一段微分(投影)圆弧,则其所对应的微分(投影)弧角dθh = khdsh。显然,取dθh绝对值的总和作为曲线的投影弧角定义是合理的。
②这一投影弧角概念反映的是投影曲线切矢方向变化的总角度。
③分别应用Meusnier定理和Euler公式 [7] 并注意到柱面横截线切线方向为最大曲率(绝对值)主方向,柱面母线方向为最小曲率(绝对值)主方向且为0,可以得到
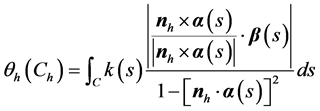 (5)
(5)
其中,k(s)为C的曲率,α(s) 为C的切矢,β(s) 为C的主法矢,nh为Πh的法矢,s为C的自然参数。
根据(1)、(3)和(5)式,可以得出,对于同一曲线,弧角≥测地弧角,而弧角和投影弧角之间的大小则不定。如果曲线为平面曲线且以其所在平面为投影平面,则三者相等。
3. 性质
性质1:伪度量
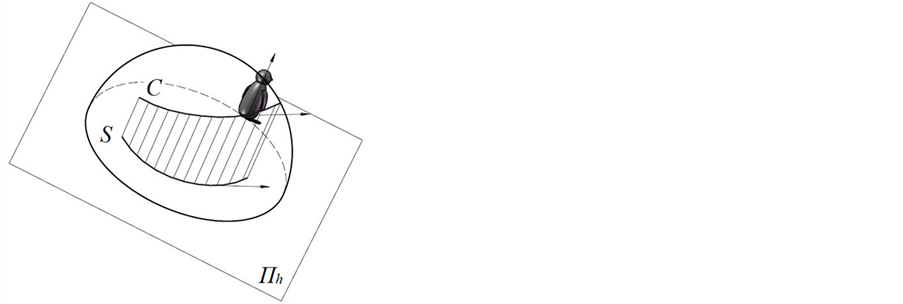
如图4所示,设C为E3中有限弧长简单正则曲线并在其上取原点并定向:若C为闭合曲线,则原点为其上任意一点,方向亦任意;若C为非闭合曲线,则原点为其上任一端点,方向离开此点进入曲线内部,则
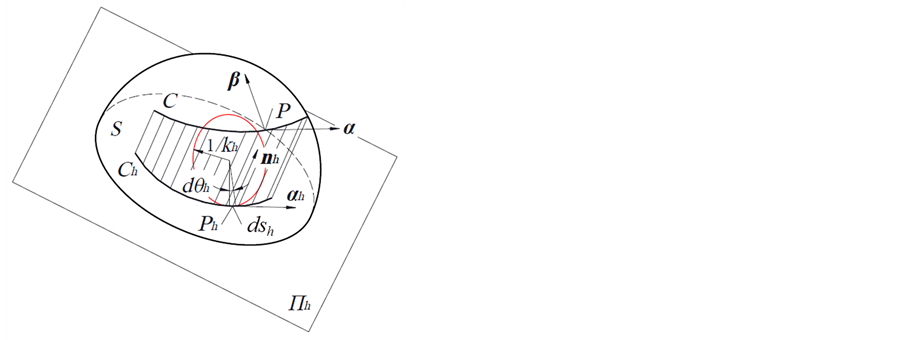
Figure 3. Projection osculating circle (red line), differential projection arc and differential projection arcangle
图3. 投影密切圆(红线所示)、微分投影圆弧与微分投影弧角
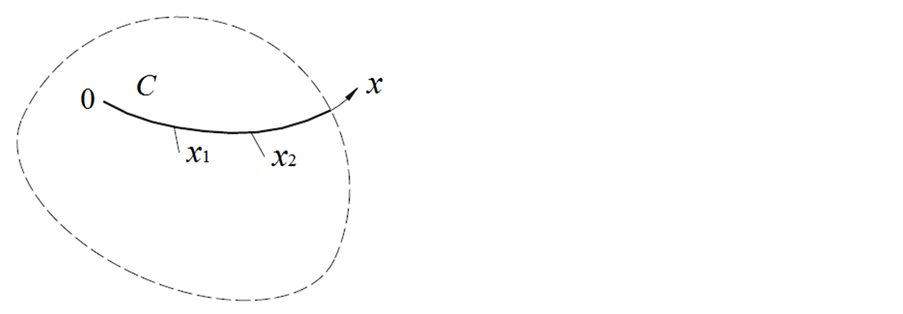
Figure 4. Angular distance traveled of a curve
图4. 曲线的角度路程

为C上原点到x点曲线段的弧角,其中,s(x)为C上原点到x点曲线段的弧长,L为C的弧长。
令
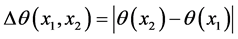 (6)
(6)
不难验证, 是一个比较C上原点分别到x1和x2点这二段曲线总弯曲程度的伪度量。注意到,
是一个比较C上原点分别到x1和x2点这二段曲线总弯曲程度的伪度量。注意到,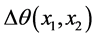 是C上x1到x2点弯曲角度的增量,因此,可称为C上x1到x2点的角度路程,其中
是C上x1到x2点弯曲角度的增量,因此,可称为C上x1到x2点的角度路程,其中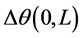 为C上原点到终点的角度路程,可称为C的角度路程。
为C上原点到终点的角度路程,可称为C的角度路程。
性质2:均匀缩放下的不变量
这是显然的,表明弧角独立于弧长,是反映曲线形状的一个度量指标。
可以得出,以上性质同样适用于测地弧角和投影弧角。
需要指出,目前所称的曲线路程是由弧长所导出的长度路程,这是一个度量。
4. 应用
如图1~3所示,假定其中三个同名曲线C为同一曲线。现在考虑三种其上固结有直角坐标系O-xyz并且原点O轨迹为C的刚体的运动:第一种,x轴正向与C切矢α(s)同向,其它二个坐标轴方向不限;第二种,x轴正向与C切矢α(s)同向,z轴正向与曲面S法矢n(s)同向,即xOy坐标平面与S的切平面Πg重合;第三种,x轴正向与切矢α(s)在投影平面Πh的投影矢量同向,z轴正向与投影平面Πh法矢nh(s)同向。显然,C的弧角,测地弧角和投影弧角分别代表了对三种刚体分别有意义的角度路程,测地角度路程和投影角度路程。可见,虽然三种刚体的长度路程相同,但它们的三种角度路程可能不同。
不难理解,如图5所示,在一定条件下,三种刚体分别代表了飞行的飞机,行驶的汽车和步行(包括缓跑)的人,其中C为飞机飞行,汽车行驶和人步行的路线,S为汽车行驶和人步行的道路路面,Πg为汽车当前所在位置路面的切平面,Πh为水平面。注意到,角度路程,测地角度路程和投影角度路程分别是飞机,汽车和人“拐弯”的结果,或者说,是人为操纵的结果。对飞机来说,“拐弯”就是偏航和俯仰(侧滚虽然也可操纵,但却独立于飞行路线的扭曲,也就是与飞行路线的挠率无关);对汽车来说,“拐弯”就是左右转向(上、下坡和侧倾由路面控制);对人来说,“拐弯”就是左右扭转身体(身体由重力控制始终向上,与路面的坡度和倾斜(在一定范围内)没有关系)。

 (a) (b) (c)
(a) (b) (c)
Figure 5. (a) An airplane flying, (b) a car going and (c) a penguin walking along a curve
图5. 沿着曲线(a) 飞行的飞机;(b) 行驶的汽车;(c) 行走的企鹅
以上可以看出弧角概念在描述物体运动中的应用价值。仔细分析起来,飞机飞行的角度路程可能意
义不大,但汽车行驶的测地角度路程和人步行的投影角度路程却有很大的意义。汽车和人走直线和经常拐弯显然大不相同:后者需要花费更多的精力,特别是拐较大的弯。例如,同样长度路程的马拉松赛跑,拐弯多成绩可能就要差一些。另外,经常拐弯能耗也要大,因为要克服阻力矩。例如,同样的长度路程,拐弯多时汽车的油耗也必定大一些。在实际操作层面,除了个别情况(如大倾斜弯曲的立交桥)外,路面大都(弯曲时)倾斜不大,利用(3)式计算测地弧角时可以忽略其中二阶小量,这样就会得出与投影角度路程(以水平面为投影面)相同的结果。也就是说,在这种情况下,只需要计算道路平面线形 [8] 的角度路程(不区分两种角度路程),而这个计算就是把左右“拐弯”的角度简单相加,不但专业人员,也容易为大众所接受(其实,人们日常生活中已经使用诸如回家的路要拐多少弯,天门山盘山公路99弯 [9] 等说法,角度路程的概念只是更进一步的定量化而已)。
在其它应用方面,相比测地弧角和投影弧角来讲,弧角的意义要大的多。例如,作为三维大弧度飞行表演的一个指标,三维大角度弯曲的立交桥的一个指标,以及三维大角度弯曲的弯管的一个指标,等。需要指出,在后两个例子中,全挠率也是一个指标。甚至,综合弧角(全曲率)和全挠率的影响,采用Darboux矢量 [10] 对弧长的积分作为指标则更全面。
5. 结语
作为圆弧弧角概念的推广,本文提出了与曲线的弧长对应的曲线弧角概念,给出了E3中弧角、测地弧角和投影弧角的定义。在此基础上,建立了与长度路程对应的曲线的角度路程、测地角度路程和投影角度路程的概念,指出它们都是伪度量。
弧角可以作为三维线状物体或对象总弯曲程度的评价指标,特别是由其可以导出道路的角度路程概念,这些都显示了其潜在的应用价值。
文章引用
李彬. 曲线的弧角概念及其应用
Concept of Arcangle of Curves and Its Applications[J]. 测绘科学技术, 2016, 04(02): 53-59. http://dx.doi.org/10.12677/GST.2016.42007
参考文献 (References)
- 1. Sullivan, J.M. (2008) Curves of Finite Total Curvature. Discrete Differential Geometry, 38, 137-161. http://dx.doi.org/10.1007/978-3-7643-8621-4_7
- 2. Qin, Y.A. and Li, S.J. (2002) Total Torsion of Closed Lines of Curvature. Bulletin of the Australian Mathematical Society, 65, 73-78. http://dx.doi.org/10.1017/S0004972700020074
- 3. 丁春华. 关于曲线全曲率的几个定理[J]. 安徽师大学报(自然科学版), 1993(16): 63-68.
- 4. Hua, L., Pan, L.B. and Lan, J. (2009) Researches on the Ring Stiffness Condition in Radial-Axial Ring Rolling. Journal of Materials Processing Technology, 209, 2570-2575. http://dx.doi.org/10.1016/j.jmatprotec.2008.06.002
- 5. Dori, D. (1995) Vector-Based Arc Segmentation in the Machine Drawing Understanding System Environment. IEEE Transactions on Pattern Analysis and Machine Intelli-gence, 17, 1057-1068. http://dx.doi.org/10.1109/34.473231
- 6. Landau, U.M. (1987) Estimation of a Circular Arc Center and Its Radius. Computer Vision, Graphics, and Image Processing, 38, 317-326. http://dx.doi.org/10.1016/0734-189X(87)90116-2
- 7. 吴大任. 微分几何讲义[M]. 北京: 高等教育出版社, 1959: 32-34, 55-57, 168, 180-181, 268-271.
- 8. 庄海涛. 公路线形设计概要[M]. 南京: 东南大学出版社, 1993: 1.
- 9. http://www.cn-zhangjiajie.cn/action/model/name/jingqu/itemid/12.html
- 10. 苏步青. 微分几何学(第二版)[M]. 北京: 高等教育出版社, 1987: 74-76.