Journal of Organic Chemistry Research
Vol.
10
No.
03
(
2022
), Article ID:
55882
,
15
pages
10.12677/JOCR.2022.103010
基于多元回归分析对乙醇偶合制备C4烯烃的 研究
陈子豪,史深圳,方娟华,陈华俊
安徽理工大学,安徽 淮南
收稿日期:2022年6月3日;录用日期:2022年9月8日;发布日期:2022年9月16日

摘要
本文针对制备收率最优的C4烯烃的问题,使用极差法,曲线拟合,回归分析等方法,建立多元线性回归,灰色关联度等模型,运用SPSS,MATLAB等软件编程,得到最优的催化剂组合和温度。通过探讨不同催化剂组合,研究与乙醇转化率、C4烯烃选择性与温度的关系,其次,在不同催化剂组合的基础上,增加了温度与不同催化剂之间的联系,同时对乙醇转化率与C4烯烃选择性大小的影响程度进行分析,结合上述步骤,选择最优的催化剂组合和温度,让C4烯烃的收率在相同的实验条件下最优。为了得到更为合理的结果,通过增加五次实验,更好的得到催化剂组合及温度对乙醇转化率以及C4烯烃的影响。最后,对模型进行了模型检验,并对模型中的可行性进行了分析,以及对本文建立的模型进行了评价。
关键词
乙醇,C4烯烃,温度,催化剂

Preparation of C4 Olefins by Ethanol Coupling Based on Multiple Regression Analysis
Zihao Chen, Shenzhen Shi, Juanhua Fang, Huajun Chen
Anhui University of Science and Technology, Huainan Anhui
Received: Jun. 3rd, 2022; accepted: Sep. 8th, 2022; published: Sep. 16th, 2022

ABSTRACT
In this paper, aiming at the problem of preparing C4 olefin with the best yield, using the range method, curve fitting, regression analysis and other methods, establish multiple linear regression, gray correlation degree model, using SPSS, MATLAB and another software programming, get the optimal catalyst combination and temperature. By discussing the different combinations of catalysts, the research and the ethanol conversion, C4 olefin selectivity and the relationship between temperature, secondly, on the basis of the different combinations of catalysts, the contact between different catalysts to increase the temperature, at the same time to ethanol conversion rate and the size of C4 olefin selectivity to influence were analyzed, and the combination of the above steps, select the optimal combination of catalyst and temperature, The yield of C4 olefins is optimal under the same experimental conditions. In order to obtain more reasonable results, five experiments were added to better obtain the influence of catalyst combination and temperature on ethanol conversion and C4 olefin. Finally, the model is tested, the feasibility of the model is analyzed, and the model established in this paper is evaluated.
Keywords:Ethanol, C4 Olefin, Temperature, Catalyst

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
C4烯烃在世界范围内被广泛地应用于化工生产等国民经济的重要领域,已经成为一种重要的化工原料 [1]。目前,国内外多以甲烷混合气和轻质石油为其制备原料,采用蒸汽裂解的传统工艺生产C4,但传统的制备方式存在着较多不足之处,除制备温度高、蒸汽用量大导致附加耗能较高外,还有所得C4产物纯度低这一致命的弱点,因此,寻求采用乙醇偶合的工艺技术进行C4烯烃制备,此工艺制备C4烯烃成本低廉,附加产物少,正在成为世界制备C4烯烃 [2] 的新兴技术。因此,研究催化耦合过程的催化剂组合设计以及对温度等变量的控制方案对优化C4烯烃耦合制备具有重大现实应用意义。
2. 不同催化剂对于乙醇转化率的影响
针对附件1所给出的21种不同催化剂的组合,可以研究出每一种催化剂组合对应的乙醇转化率、C4烯烃的选择性与温度的关系。本文主要通过相关性分析,分别求解其相关系数,得出拟合优度最好的回归方程 [3]。针对附件二中某催化剂在同一温度下不同时间的测试结果进行分析。采取同第一部分相同的方法进行曲线拟合,运用MATLAB软件将拟合出的曲线与第一部分的曲线方程进行比对,并用附件一的数据进行检验分析,用单位时间曲线的变化率对附件2结果进行分析。
2.1. 数据可视化处理
针对附件1首先对数据进行可视化处理,各催化剂组合在不同温度下关于C4烯烃的选择性(见图1)和乙醇转化率(见图2)的散点图如下。
观察散点图发现温度在400摄氏度时的数据仅有一个,其他温度处的乙醇转化率的值没有异常。因此在本文的后续对温度的分类中主要考虑250、275、300、325、350这五种分类方式。
2.2. 绘制散点图
以A1为例,根据附件1中提供的数据数据,借助SPSS软件,绘出乙醇转化率与温度关系(见图3),以及C4烯烃的选择性(见图4)与温度关系的散点图如下图所示:

Figure 1. Scatter diagram of C4 olefins selectivity at different temperatures
图1. 不同温度C4烯烃选择性散点图
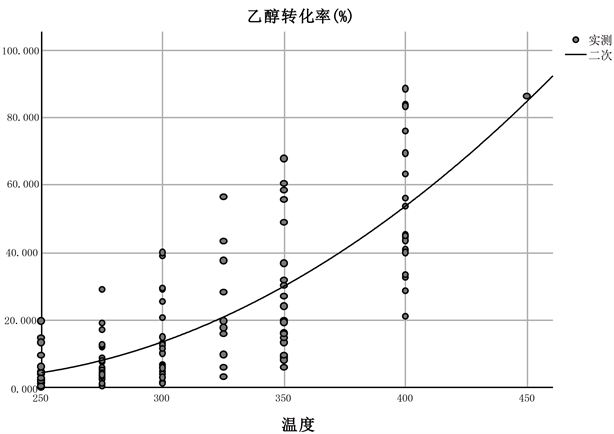
Figure 2. Scatter diagram of ethanol conversion at different temperatures
图2. 不同温度乙醇转化率散点图
故乙醇转化率、C4烯烃的选择性存在明显的相关性,对样本进行相关性分析 [4],可确定回归模型。
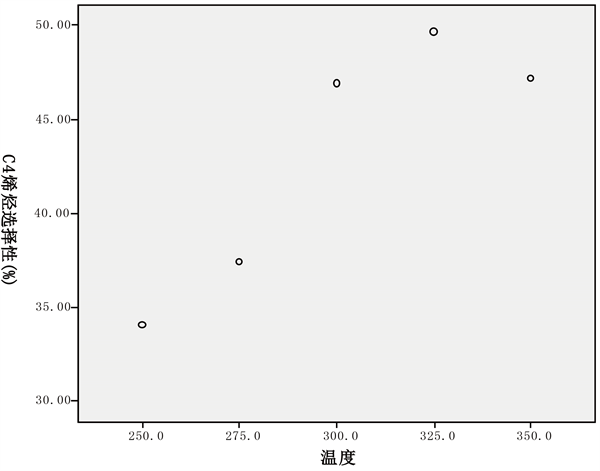
Figure 3. Scatter diagram of the relationship between A1 ethanol conversion rate and temperature
图3. A1乙醇转化率与温度关系散点图

Figure 4. Scatter plot of A1C4 olefins selectivity and temperature
图4. A1C4烯烃选择性与温度关系散点图
2.3. 曲线拟合
由于样本很小,本文采取直接曲线拟合,利用SPSS软件分别对A1的乙醇转化率和C4烯烃的选择性与温度及进行相关性分析,得到乙醇转化率与温度的皮尔逊相关系数矩阵(见表1)以及C4烯烃的选择性与温度的皮尔逊相关系数矩阵(见表2)如表:
Table 1. Pearson phase correlation between ethanol conversion and C4 olefin selectivity
表1. 乙醇转化率与C4烯烃选择性皮尔逊相关系数表
Table 2. Pearson phase correlation between ethanol conversion and C4 olefin selectivity
表2. 乙醇转化率与C4烯烃选择性皮尔逊相关系数表
在表1和表2中,由皮尔逊相关系数可知 [1],数据与数据本身相关性为1,乙醇转化率、C4烯烃的选择性与温度的相关系数分别0.965和0.887,存在相关性,建立回归模型进行分析。
运用C语言编程,导入附件1的数据,分析上述不同温度乙醇转化率散点图和不同温度C4烯烃转化率散点图(见图5)可得:
根据编程结果可得到各个拟合曲线的方程及拟合度。
线性方程:
乙醇转化率:
C4烯烃的选择性:

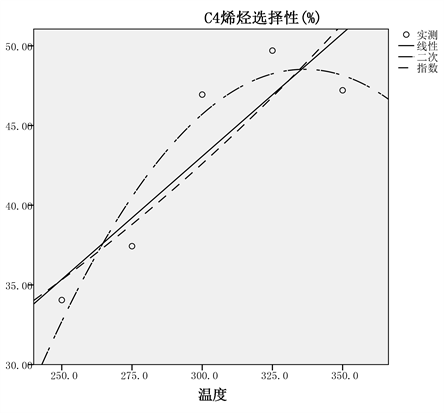
Figure 5. Comparison of fitting curves of ethanol conversion and C4 olefins selectivity
图5. 乙醇转化率和C4烯烃选择性的拟合曲线对比图
根据拟合的结果图,可以看到拟合的线性回归方程较好,相关系数R2分别为0.932,0.787,曲线参数量F分别为41.230,11.079,大部分散点有规律地分散在曲线上或者上下两侧。
二次方程:
乙醇转化率:
C4烯烃的选择性:
结果显示,回归方程显著,拟合优度系数R2分别为0.980,0.916,曲线参数量F分别为48.377,10.899,说明模型与数据拟合优度较好。
指数方程:
乙醇转化率:
C4烯烃的选择性:
结果显示,回归方程显著,相关系数R2分别为0.957,0.794,曲线参数量F分别为67.522,11.531,表明拟合出来的方程 [5] 与数据符合较好。
第二部分的求解:
针对350摄氏度时某催化剂的测试结果,本文首先采用与第一部分相同的分析方法,对数据进行相关性分析。同样由于样本过少,本文采用直接拟合的方式进行直接拟合。以时间为横坐标,乙醇转化率以及各产物在总产物之间的占比作为纵坐标,进行曲线拟合。
曲线拟合:
运用SPSS软件对时间和乙醇转化率及其生成物进行曲线拟合,拟合优度 , ,显著性 ,具有统计学意义,拟合结果较好,二次回归方程显著。部分时间与变量之间的拟合图(见图6)如下所示:


Figure 6. Curve fitting diagram of products and time in Annex 2
图6. 附件2部分产物与时间的曲线拟合图
2.4. 结果分析
运用MATLAB软件进行分析,对附件二拟合出的方程与附件一拟合出的方程进行比对,根据附件二的反应生成结果,得出附件二的催化剂组合为A3和A4。通过图像分析,以及对样本数据进行两点间的距离计算,得出的单位时间内乙醇转化率以及各生成物在单位时间的变化率,分别为:0.114、0.001、0.027、0.0086、0.0468、0.034、0.0302。由此可得 [6] 乙醇的转化率随时间的影响较大,其次为碳数为4-12脂肪酸,乙烯的选择性影响较小。根据数据的拟合曲线也可以得出C4烯烃的选择性随时间变化是先减少后增加的,存在含量占比的最低点。在后续分析中为了C4烯烃收率最高,该点应该规避。
3. 不同催化剂和温度对于乙醇转化率和C4烯烃的选择性影响
这部分是在上一部分的基础上,增加了不同催化剂组合及温度的关联性,再对乙醇转化率和C4烯烃的选择性进行分析。采取与上部分相同的分析方式,但在探讨不同催化剂的影响的前提下,因此需要对数据进行处理,对催化剂的成分种类进行拆分,更好的分析催化剂中的各个成分对影响C4烯烃收率的两个成分进行分析。为求解出影响的大小,本文采用灰色关联度分析模型,控制变量,分别分析温度相同时不同催化剂种的成分对乙醇转化率和C4烯烃选择性的影响以及催化剂相同,温度不同时对这两种成分的影响。
3.1. 数据预处理
考虑到A,B为两种不同的装料方式,本文将装料方式Ι记为1,装料方式Π记为2。催化剂的拆分以“200 mg 1 wt% Co/SiO2-200 mg HAP-乙醇浓度0.9 ml/min”为例,将其拆分为Co/SiO2含量、Co负载量、HAP含量、Co/SiO2和HAP装料比,石英砂含量,这五种成分。分别记作200、1、200、1.00、0。
处理后的部分数据如下表(见表3)所示:
Table 3. Data after processing in Appendix 1
表3. 附件1处理后的数据
3.2. 相关性分析
利用SPSS软件对处理后的数据进行双变量相关性分析,结果得出这6种变量之间的相关性极强,且都通过检验。具体结果见附录。
灰色关联度分析模型的求解:
首先将分辨系数带入公式,用编程软件编程可以计算得到Co/SiO2含量、Co负载量、HAP含量、Co/SiO2和HAP装料比,石英砂含量分别与乙醇转化率和C4烯烃的选择性的关联系数。然后计算Co/SiO2含量、Co负载量、HAP含量、Co/SiO2和HAP装料比与乙醇转化率和C4烯烃的选择性的关联度 [7],如表4所示:x11表示装料方式、x12表示Co/SiO2含量、x13表示Co负载量、x14表示HAP含量、x15表示石英砂含量、x16表示Co/SiO和HAP 装料比、x17表示乙醇浓度;r(1)表示C4烯烃的选择性、r(2)表示乙醇转化率。
Table 4. Results of correlation degree
表4. 关联度结果
结果分析:
对表格4其中数据分析 [3] 如下:
温度固定
温度固定的情况下不同催化剂组合对乙醇转化率的影响:
由关联度表格得出:
即:HAP含量 > Co/SiO2含量 > Co负载量 > Co/SiO和HAP装料比 > 装料方式 > 乙醇浓度 > 石英砂含量
温度固定的情况下不同催化剂组合 [8] 对C4烯烃选择性的影响:
由关联度表格得出:
即:Co/SiO和HAP装料比 > Co/SiO2含量 > 乙醇浓度 > HAP含量 > 装料方式 > Co负载量 > 石英砂含量
催化剂固定
温度改变时,催化剂成分相同情况下对乙醇转化率的影响:
温度改变时,催化剂成分相同情况下对C4烯烃选择性的影响:
由关联度可以得出,温度改变时对乙醇转化率来说均是乙醇浓度的影响最大,其次是Co/SiO2含量,且均是石英砂的含量影响最少。而对C4烯烃选择性的影响,在400摄氏度时乙醇浓度的影响才较为明显,低于300摄氏度起决定性作用的是Co/SiO和HAP装料比,低于300~400摄氏度之间起主要作用的是HAP含量,次级影响因素和最小影响因素均为Co/SiO2含量和石英砂含量。
4. 最优催化剂组合和温度
第一部分要求找出最优的催化剂组合与温度,保证在相同实验条件下使得C4烯烃的收率尽可能高。根据第一部分和第二部分对催化剂成分和温度的关系的分析,得出的不同温度下乙醇转化率与C4烯烃选择性与温度的函数关系式,建立优化 [9] 函数。其中,目标函数为C4烯烃的收率,决定最优解的决策变量分别为催化剂组合(Co/SiO2含量、Co负载量、HAP含量、Co/SiO2和HAP装料比、石英砂含量)以及温度。运用多元线性回归方程进行最佳参数的设置,将回归方程作为约束变量的一部分。通过MATLAB软件,采用粒子群算法 [1] [2] 对约束函数进行极值寻优,求解即可得到最佳的催化剂成分组合和温度。
第二部分是在第一部分的基础上对温度条件加以限制,即在约束条件中对温度进行约束即可。
首先,设C4烯烃的选择性为因变量 ,将Co/SiO2含量、Co负载量、HAP含量、Co/SiO2和HAP装料比、石英砂含量和温度这六种回归变量,这六种决策变量分别设为 、 、 、 、 、 。
回归方程系数估计结果(见表5)。
Table 5. Results of regression coefficient equation
表5. 回归系数方程结果
统计量:R2 = 0.325、F = 24.325、P < 0.0001、s2 = 1.1137。
5. 结论
从回归系数表中可以观察到,温度变量在解释两个乙醇转化率、C4烯烃回归方程中起到了极为重要的作用,当温度和其它自变量相组合时,对因变量的结果也会产生重要的影响。且Co/SiO2与HAP的装料比的解释能力在两个回归方程中差别不大,均为正相关。而Co负载量在乙醇转化率中基本没有解释性,但是在C4烯烃选择性中有较强的负相关解释性。而乙醇浓度则对乙醇转化率起负相关解释性,而对C4烯烃选择性很少有解释性。从回归系数图中可以观察到,温度变量在解释两个乙醇转化率、C4烯烃回归方程中起到了极为重要的作用,当温度和其它自变量相组合时,对因变量的结果也会产生重要的影响。且Co/SiO2与HAP的装料比的解释能力在两个回归方程中差别不大,均为正相关。而Co负载量在乙醇转化率中基本没有解释性,但是在C4烯烃选择性中有较强的负相关解释性。而乙醇浓度则对乙醇转化率起负相关解释性,而对C4烯烃选择性很少有解释性。
文章引用
陈子豪,史深圳,方娟华,陈华俊. 基于多元回归分析对乙醇偶合制备C4烯烃的研究
Preparation of C4 Olefins by Ethanol Coupling Based on Multiple Regression Analysis[J]. 有机化学研究, 2022, 10(03): 96-110. https://doi.org/10.12677/JOCR.2022.103010
参考文献
- 1. 李逸然, 宫豪杰, 李琦, 王丽莎. 乙醇耦合制备C4烯烃问题研究[J]. 山东化工, 2022, 51(10): 85-88.
- 2. 余胜威. MATLAB优化算法案例分析与运用[M]. 北京: 清华大学出版社, 2002.
- 3. 范晨, 王斌. 基于灰色关联法的森林火灾危险性风险评价[J]. 测绘科学, 2010(S1): 110-112.
- 4. 赵峰. 典型相关分析算法理论及其在模式分类中的应用[D]: [硕士学位论文]. 西安: 西安电子科技大学, 2005.
- 5. 张媛, 金一冉, 李霄. 基于机器学习和多元非线性拟合的乙醇偶合制备C4烯烃研究[J]. 科学技术创新, 2022(16): 177-180.
- 6. 王艺颖, 石一焜, 张红. 基于回归分析的乙醇制备C4烯烃试验设计[J]. 中国新技术新产品, 2022(3): 8-10.
- 7. 李明, 于剑波, 逯怡博, 王国欣. 基于回归分析模型探究乙醇偶合制备C4烯烃[J]. 江西化工, 2021, 37(6): 92-94.
- 8. 吕绍沛. 乙醇偶合制备丁醇及C4烯烃[D]: [硕士学位论文]. 大连: 大连理工大学, 2018.
- 9. 李韶伟, 王宇杰, 熊浪, 黄圣淇. 乙醇偶合制备C4烯烃的优化模型[J]. 台州学院学报, 2021, 43(6): 26-32.
附录
附件1
