Journal of Aerospace Science and Technology
Vol.
06
No.
03
(
2018
), Article ID:
27049
,
8
pages
10.12677/JAST.2018.63005
Study on Mechanical Characteristics of Space Elevator
Man Ru1, Mingwei Yin2
1The High School Affiliated to Renmin University of China, Beijing
2Department of Aerospace Engineering, Tsinghua University, Beijing
Received: Sep. 8th, 2018; accepted: Sep. 23rd, 2018; published: Sep. 30th, 2018

ABSTRACT
Space elevator is a new way to transporting loads to space at a low cost, which is one of the most important development trends. Based on the method of theoretical mechanics, this paper gives a discussion of the relationship between the location of the space station and the length of the elevator. For some designs of the space elevator, this paper discusses the distribution of stress and points at the position and value of the largest stress. Finally, the lowest energy and the lateral controlling impulse are calculated when a unit load is transported to space.
Keywords:Space Elevator, Mechanical Characteristics, Stress Distribution, Controlling Impulse
太空电梯力学特性分析
儒曼1,印明威2
1中国人民大学附属中学,北京
2清华大学航天航空学院,北京
收稿日期:2018年9月8日;录用日期:2018年9月23日;发布日期:2018年9月30日

摘 要
太空电梯是一种以低成本将有效载荷运送至太空的设想,是未来航天领域发展的重要方向之一。本文对太空电梯一些力学特性进行了计算,分析了太空站的选址与太空电梯长度之间的关系并给出了太空站选址的方法;针对几种典型的方案,本文给出了太空电梯的应力分布情况并得到了最大应力的位置与大小;最后,本文计算了单位载荷运送至空间站所需的最低能量以及侧向控制冲量。为后续继续开展太空电梯的设计工作提供参考。
关键词 :太空电梯,力学特性,应力分布,控制冲量

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
自从1957年苏联发射了世界上第一颗人造地球卫星开始,人造地球卫星已被用于人类生活的各个领域,如通信、测量、导航等等。随着社会的不断发展,人类对航天任务的要求变得越来越丰富多彩,未来的航天活动也会越来越频繁,甚至可能成为一种日常普普通通的活动。在这样一种情景之下,如何将卫星或者其它航天器更加高效廉价的运送到太空中就成为我们不得不考虑的问题。传统的运载火箭发射成本昂贵、周期长,不适用于未来频繁、大量、低价格的向太空运送物资的需求,这就对地球表面进入太空的方式从经济以及效率两方面提出的新的需求。为了满足这样一种需求,太空电梯的概念被重新提了出来,并得到了各国科研机构的研究与关注 [1] - [8] 。
早在19世纪末期,航天之父齐奥尔科夫斯基就提出过太空电梯的设想,但是当时,太空电梯对建造材料的要求以及巨额的建造花费使人们望而却步。但在今天,科学技术的发展已经使“太空电梯”由不可能变为可能。世界各国的许多企业和研究机构,如日本的大林组建筑公司,美国电梯港集团公司、俄罗斯萨马拉太空大学等,都已经开始提出“太空电梯”的设计方案。日本建筑公司大林组设想从地球表面伸出一条缆线连接到地球同步轨道的太空站,另外在太空站外侧伸出更长的缆绳以及一块平衡的铅坠作为配重,其预计整个太空电梯的长度约为9.6万千米,并希望在2030年左右开始进行太空电梯的建设。在其计划中,太空电梯的造价是十分昂贵的,如何使太空电梯的总长度最小也是亟需解决的问题。
太空电梯是指从地球表面连接到空间站的一条通道,通过这条通道可以将地球上的资源运送到空间站进行处理。太空电梯的使用可以大大降低从地球表面向太空运送物资的价格,据估计,单位质量的有效载荷被运送到GEO轨道仅需要500美元,这与传统运载火箭相比要降低两个数量级。另外,太空电梯还可以更加高效的利用太阳能,并以此减少太空电梯在运行过程中所消耗的能源,这样又降低了传统运载火箭在爆炸喷射时所带来的危险。太空电梯在无特殊情况时可以随时向太空运输载荷,减少了运载火箭等待发射窗口所需要的时间 [9] [10] 。
太空电梯的设计是一个具有挑战性的项目,但其中也蕴含着巨大的机遇。太空电梯的建成,将会对人类太空探索、能源利用以及旅游业等领域产生革命性的影响。通过太空电梯,我们不仅可以低成本地在地球与太空站之间运输补给资源,还可以更便捷地从地球向太空站输送航天器以及燃料,并在太空站完成航天器的发射。与地面直接发射运载火箭相比,从太空站发射航天器可以节省很大一部分的发射燃料,这对我们进行深空探测以及将来的太空旅游大有助益。
地球的自转与引力的作用对太空站的选址以及电梯骨架的力学性能都提出了新的要求,一方面,要保持太空电梯与空间站与地球表面的相对静止;另一方面,要考虑通过骨架在太空中随地球自转而旋转时所受到的拉力。空间站位置的选取与电梯骨架的受力是息息相关的,本文将讨论空间站设置在不同位置时太空电梯为保持稳定所需要的条件,计算空间站的位置与最终电梯长度之间的关系,并给出几种典型方案下电梯的应力分布情况,讨论了电梯舱在运行过程中所需要的控制条件以及最低的能量,为太空电梯的发展提供一些理论上的讨论。
2. 太空站位置与电梯长度的分析
2.1. 太空站在地球同步轨道上
为了保持空间站与地球的相对位置不变,最直接的想法是将太空站设置在地球的同步轨道上。此时太空站受到地球的引力与惯性离心力相互抵消,与地球表面的相对位置保持不变并且对太空电梯的骨架没有额外的作用力,因此在分析太空电梯骨架受力时就不需考虑太空站的作用。
太空电梯骨架连接地球表面与太空站,受到地球引力与惯性离心力的作用。为了尽量保证地球表面与太空电梯连接的基站的安全,可以设计太空电梯的长度来使得地球引力与惯性离心力相互平衡,从而使得太空电梯对地球表面也不存在作用力。下面将计算在上述情形下太空电梯所需要的长度。
如图1,Re为地球半径, 为地球自转角速度,R0为太空站到地心的距离,L为太空电梯的配重部分(否则,地球引力要大于惯性离心力,造成地球表面受到的压力过大)。地球对太空电梯的引力F1为:
(1)
其中G为引力常数、M为地球质量、 为太空电梯的线密度。
太空电梯所受到的惯性离心力F2为:
(2)
由于空间站处于地球同步轨道上,所以满足如下约束:
(3)
所以,根据太空电梯在F1和F2的作用下平衡,可以计算得到太空电梯配重部分的长度:
(4)
代入数据可以得到 。与同步轨道到地心的距离 相比,太空电梯配重段的距离明显要长的多。但是太空电梯配重段的距离越短越好,这样可以尽量降低空间碎片击中太空电梯的风险。下面讨论了通过将太空电梯配重段改用不同的材料来减少配重段长度的方法。
设 为太空电梯从地面到太空站区间的线密度, 为太空电梯配重段的线密度,令 。地球对太空电梯的引力F1为:
(5)
太空电梯所受到的惯性离心力F2为:
(6)

Figure 1. The diagram of space elevator
图1. 太空电梯示意图
根据公式(3) (5) (6)以及 可以得到如下关于L的约束方程:
(7)
从图2(a)中可以看到,随着电梯材料线密度比k的增加,电梯配重段的长度在逐渐的减小。这从物理意义上是不难理解的,k的增加表示电梯配重段的线密度在变大,因此使用更短的配重电梯长度就可以实现最终的配平。
2.2. 太空站不在地球同步轨道上
为了进一步减少电梯配重段的长度以及电梯的总长度,可以将太空站设置在比地球同步轨道高的轨道上。这时太空站仍按照地球自转的角速度运行,其受到向外的惯性离心力势必要大于指向地心的地球引力,进而对太空电梯产生一个沿径向向外的作用力,起到了电梯配重段的作用,因而可以减小电梯配重段的长度。
在这里仍然采用两端电梯材料不同的方案,所以公式(5) (6)仍然是成立的,但是由于此时太空站没有在地球同步轨道上,所以公式(3)就不再成立了。与2.1节中的讨论相比,太空电梯不再是仅仅受到F1和F2的作用,还会受到太空站对太空电梯向外的拉力F3:
(8)
由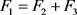 可以得到一下关于电梯配重段长度L的约束:
可以得到一下关于电梯配重段长度L的约束:
(9)
其中 表示地球同步轨道的高度、 表示太空站质量与电梯骨架线密度之比(是表征太空站质量的等效高度)。目前国际太空站的质量约为400t,所以下面的计算中m取为400t;从地球表面到太空站之间的电梯段理想的材料为碳纳米管材料 [11] ,其密度约为 ,所以估测其线密度约为16 kg/m,这样,可以得到 。
根据公式(9),可以计算得到k、R0取不同值时,电梯配重段长度L的大小,据此将计算结果展示在图2中。从图2(a)中可以发现,随着太空站布置在更高的轨道上,需要的配重电梯的长度就会减小;图2(b)中显示在低电梯材料线密度比(k < 1.5)的情况下,可以通过将太空站布置到更高的轨道的方法实现电梯总长度的减小,但是对于高电梯材料线密度比(k > 3)的情况,太空站布置在更高的轨道会得到适得其反的效果。这是因为,在低电梯材料线密度比的情况下,如两端电梯密度相同时,太空站会对电梯有沿径向向外的作用力,确实可以减少对配重电梯的需求;但是在高电梯材料线密度比的情况下,向更高轨道
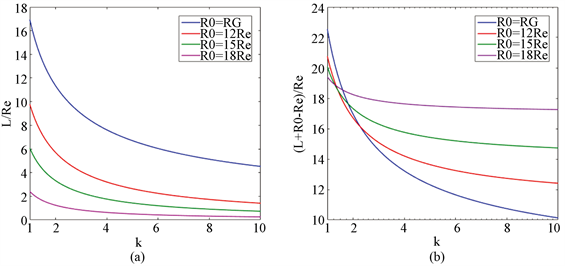
Figure 2. The relationship between the length of the whole elevator, the length of the counterweight elevator and the location of space station, the ratio of different materials’ density
图2. 电梯总长度、配重段长度与太空站位置、电梯材料线密度比之间的关系
布置太空站,会使得从地球表面到太空站之间的低密度电梯长度增加,增加的低密度电梯的长度要大于减小的高密度电梯的长度,因而电梯的总长度会反常增加。
从地球表面到太空站之间的电梯段的材料选为为碳纳米管材料,其密度 约为1.6 × 103 kg/m3;配重电梯段的材料选为钛合金,其密度 约为4.51 × 103 kg/m3;在这种情况下电梯材料线密度比k为2.82。图3显示了k = 2.82时,太空站位置对太空电梯总长度的影响,可以看出,当 时,太空电梯的总长度达到最小值,约为14.69Re。我们可以根据这一规律来选择太空站的位置,当电梯材料线密度比选定之后,将太空站布置到适当的位置,使得太空电梯的总体长度最小。
3. 太空电梯径向方向应力分布
对于太空电梯的建设,除了需要计算使其平衡所需的长度外,还需要分析电梯各处的应力分布情况,这对我们判断电梯的骨架材料是否合格十分重要。下面采用第2节中所述的一般的电梯模型,即采用两段材料不同的电梯、太空站的位置未定,以此来推导一般性结论。
下面分析在距离地心位置为R处的电梯微元的受力情况。从地球表面到距离地心位置为R处之间的电梯作为一个整体,其主要受到三种作用力:地球对其的引力、旋转坐标系下的惯性离心力以及外侧电梯沿径向向外的作用力。若R > R0,还会受到太空站向外的拉力。计算电梯微元的受力情况,就是计算电梯之间的相互作用力,也就是计算上述所说的外侧电梯沿径向向外的作用力,因此该作用力可以得到下述表达式:
(10)
再由正应力公式 得到应力的最终表达式:
(11)
我们对下述四种方案的应力分布情况给出了计算:
1) 太空站布置在地球同步轨道上,两端电梯采用相同材料( );
2) 太空站布置在地球同步轨道上,两端电梯采用不同材料( );
3) 太空站布置在8.36Re上,两端电梯采用相同材料( );
4) 太空站布置在8.36Re上,两端电梯采用不同材料( )。
图4比较了四种方案的应力分布情况,从图中可以看出,当 时,各个方案的应力分布是相同的,这是因为在在地球同步轨道高度以下的电梯部分,各方案所用的电梯材料都是相同的,为碳纳米管材料;当 时,正应力达到最大值,约为77.5 GPa,也就是说,不管是何种方案,在地球同步轨道高度处的太空电梯都会受到最大拉应力的作用,对于碳纳米管材料,该处受到的拉应力约为77.5 GPa。对于理想结构的碳纳米管材料,其抗拉强度可到达800 GPa,可见由碳纳米管材料建造的太空电梯,从应力的角度看是满足要求的。从图4中看到,对于太空站布置在8.36Re上的两种方案,应力在8.36Re处会存在不连续的情况,这是由于太空站在8.36Re的位置会对太空电梯产生一个集中力的作用,因而该处的应力不连续。
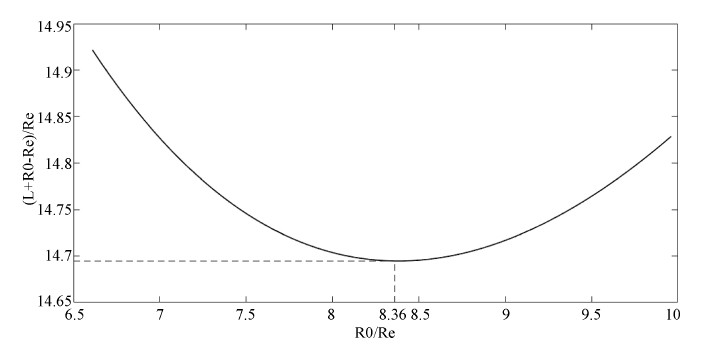
Figure 3. The relationship between the length of the whole elevator and the location of the space station
图3. 太空电梯总长度与太空站位置的关系
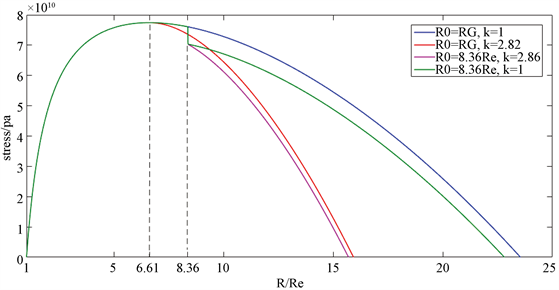
Figure 4. The stress distribution of the space elevator
图4. 太空电梯应力分布图
4. 电梯运送载荷的特性分析
4.1. 单位质量载荷运送至太空站所需能量的计算
载荷在太空电梯中运行,沿径向受到三种力的作用:地球对电梯舱的引力f1、旋转坐标系下产生的惯性离心力f2、太空电梯对单位质量载荷的作用力f3。其中f1和f2为有势力,可以计算得到单位质量载荷从地面被运送至太空站,其势能的增量为:
(12)
所以太空电梯将单位质量载荷送至太空所需要的最小能量为:
(13)
分析公式(13)可以得到,当太空站处于地球同步轨道的位置时,将单位质量的载荷从地球表面运送到太空站所需要的最小能量是最大的;随着太空站布置到更高的轨道上,将单位质量载荷运送到太空站所需要的最小能量会逐渐变小。
4.2. 电梯运送载荷时太空站控制所需冲量
载荷从地面运送至太空站时,除了电梯需要克服载荷的重力势能与离心势能外,还需要对太空站进行一定的控制。在地球自转旋转坐标系中,运行中的载荷除了受到径向的地球引力、离心力和电梯的牵引力外,还会受到侧向的科里奥利力。这一侧向的科里奥利力需要太空站与电梯地面之间的基站共同抵消。太空站在单位载荷从地面运送至太空站的整个过程中,需要的提供的侧向总冲量为:
(14)
从公式(14)中可以看出,太空站所需要提供的侧向总冲量仅与太空站到地球表面的距离有关,因此,太空站距离地球表面越近,载荷运送至太空站时,太空站所需提供的侧向总冲量就越小。当太空站设立在同步轨道高度( )时,可以得到将单位载荷运送至太空站所需提供的侧向冲量约为2614 N∙s/kg。
5. 结论
本文分析了太空电梯的基础力学特性,对太空站位置的选取以及太空站的长度进行了讨论,并对几种典型方案分析了应力分布情况,明确了载荷运送至太空站所需的最小能量以及此过程中太空站的控制冲量,研究结果表明:
1) 通过增加太空电梯配重段的线密度,可以减小电梯的总长度;
2) 对于一定的电梯材料线密度比,在比地球同步轨道更高的轨道上,存在一个太空站的位置,使得电梯总长度最小;
3) 在地球同步轨道高度的位置,太空电梯所受到的拉力最大;对于碳纳米管材料,该处的应力约为77.5 GPa;
4) 载荷运送至太空站所需能量以及运送过程中太空站所需要的控制冲量,仅与太空站的位置有关,且太空站轨道高度越低,所需的控制冲量越小。
太空电梯可以满足低成本、高效率、常态化的太空任务需求,对人类未来进一步探索宇宙世界有着重要的意义。太空电梯的发展必将引起航天领域的巨大变革。
文章引用
儒 曼,印明威. 太空电梯力学特性分析
Study on Mechanical Characteristics of Space Elevator[J]. 国际航空航天科学, 2018, 06(03): 38-45. https://doi.org/10.12677/JAST.2018.63005
参考文献
- 1. Cohen, S.S. and Misra, A.K. (2007) Elastic Oscillations of the Space Elevator Ribbon. Journal of Guidance Control and Dynamics, 30, 1711-1717. https://doi.org/10.2514/1.29010
- 2. Cohen, S.S. and Misra, A.K. (2009) The Effect of Climber Transit on the Space Elevato Dynamics. Acta Astronautica, 64, 538-553.
- 3. Woo, P. and Misra, A.K. (2014) Energy Considerations in the Partial Space Elevator. Acta Astronautica, 99, 78-84. https://doi.org/10.1016/j.actaastro.2014.02.013
- 4. Ishikawa, Y., Otsuka, K., Yamagiwa, Y. and Doi, H. (2018) Effects of Ascending and Descending Climbers on Space Elevator Cable Dynamics. Acta Astronautica, 145, 165-173. https://doi.org/10.1016/j.actaastro.2018.01.031
- 5. Knapman, J.M. and Swan, P.A. (2014). Design Concepts for the First 40 km a Key Step for the Space Elevator. Acta Astronautica, 104, 526-530. https://doi.org/10.1016/j.actaastro.2014.06.004
- 6. Quine, B.M., Seth, R.K. and Zhu, Z.H. (2009) A Free-Standing Space Elevator Structure: A Practical Alternative to the Space Tether. Acta Astronautica, 65, 365-375. https://doi.org/10.1016/j.actaastro.2009.02.018
- 7. 李蒙, 陈伟跃, 杨胜, 等. 月球天梯力学特性研究[J]. 中国空间科学技术, 2016, 36(3): 63-69.
- 8. 宋海蓝, 蒋婷婷, 周莉, 等. 月球天梯系统模型建立和太空舱运动的能耗计算[J]. 机械管理开发, 2018(4): 1-4.
- 9. 汪小卫, 鲁宇, 刘丙利, 等. 天梯技术研究进展[J]. 导弹与航天运载技术, 2015(2): 41-44.
- 10. 张普卓, 汪小卫, 刘丙利, 等. 天梯系统指标初步研究[J]. 导弹与航天运载技术, 2016(3): 5-8.
- 11. 刘剑洪, 吴双泉, 何传新, 等. 碳纳米管和碳微米管的结构、性质及其应用[J]. 深圳大学学报理工版, 2013, 30(1): 1-11.