Nuclear Science and Technology
Vol.
07
No.
03
(
2019
), Article ID:
31203
,
8
pages
10.12677/NST.2019.73012
Development and Validation of Numerical Simulation Program for MHD Flow and Heat Transfer in Liquid Metal Blanket of Fusion Reactor
Jiajia Han1,2,3, Weihua Wang1,2*
1Institute of Plasma Physics, Chinese Academy of Sciences, Hefei Anhui
2University of Science and Technology of China, Hefei Anhui
3PLA Army Academy of Artillery and Air Defense, Hefei Anhui

Received: June 17th, 2019; accepted: July 2nd, 2019; published: July 9th, 2019

ABSTRACT
The effect of magnetohydrodynamic effect on the flow and heat transfer of liquid metal in liquid blanket of fusion reactor is studied. A numerical simulation program of MHD flow and heat transfer distribution is developed. The flow and heat transfer phenomena in liquid blanket of fusion reactor are simulated by numerical method. The numerical simulation program is based on the four-step projection method to calculate the flow field distribution in the blanket under strong magnetic field. The temperature distribution is obtained by using the finite volume method. The results of numerical simulation are verified by standard examples and energy conservation methods. It provides a reference for the study of the flow and heat transfer characteristics of liquid metals in the blanket of fusion reactor.
Keywords:MHD, Heat Transfer, Temperature Distribution, Numerical Method
聚变堆液态金属包层MHD流动和传热数值模拟程序开发与验证
韩佳佳1,2,3,汪卫华1,2*
1中国科学院合肥物质科学研究院等离子体物理研究所,安徽 合肥
2中国科学技术大学,安徽 合肥
3陆军炮兵防空兵学院基础部物理教研室,安徽 合肥

收稿日期:2019年6月17日;录用日期:2019年7月2日;发布日期:2019年7月9日

摘 要
本文研究了磁流体动力学效应对聚变堆液态包层中液态金属流动和传热的影响,开发了MHD流动与传热分布数值模拟程序,采用数值方法对聚变堆液态包层中的流动传热现象进行了模拟。该数值模拟程序基于4步投影法计算强磁场下包层中的流场分布,利用有限体积法得到了流道中的温度分布,并通过标准算例和能量守恒的方法对数值模拟的结果进行验证,为开展聚变堆包层中液态金属的流动与传热特性的研究提供了参考。
关键词 :MHD,热传输,温度分布,数值方法

Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
聚变堆包层是聚变反应堆中的重要部件,主要完成包括能量转换、氚增殖和辐射屏蔽等功能。按照氚增殖剂的形态,包层分为固态增殖包层和液态增殖包层。与固态包层相比,液态包层具有结构简单,氚增殖能力强,可以实时在线提氚的优点,因而成为聚变包层概念设计的主要候选方案之一。国际上提出了一系列液态金属包层方案,这些包层中,一般将液态铅锂合金作为冷却剂和中子/氚增殖材料 [1] [2] 。
由于处在强磁场环境下,液态金属的流动会产生感应电动势,进而产生感应电流,感应电流与磁场的相互作用会产生阻碍流体运动的洛仑兹力,导致了磁流体动力学(MHD)效应。MHD效应增加了液态金属的流动压降,影响着流动金属的流动与传热效应。Shercliff与Hunt [3] [4] 首先提出了矩形管道中完全发展MHD流动的解析解,成为以后数值计算结果的标准算例。倪明玖 [5] 基于电势法,在非结构同位网格上利用相容守恒格式发展了求解MHD流动的数值算法,能准确计算出管道中液态金属的流动分布。Smolentsev [6] 基于磁感应法开发了可以求解二维高哈特曼数下的MHD流动程序,并将其应用于有FCI插件等复杂流道的分析。但由于聚变堆包层中存在着磁场、流场和温度场的相互耦合作用,目前关于MHD效应对温度场影响的研究还很少。为优化包层模块的设计,本文提出了一种针对包层增殖区矩形流道液态金属MHD流动温度分布的数值模拟方法。该方法主要利用相容守恒格式在非均匀网格上得到的速度分布 [5] ,根据聚变堆包层的特点,设置合理的边界条件,将动量方程与能量方程分别求解。其中得到的速度分布结果通过与解析解对比进行验证,温度分布结果通过能量守恒的方法验证。
2. 控制方程与数值方法
2.1. 控制方程
聚变堆包层矩形流道中充分发展的不可压缩稳态流动数值模拟由描述流体流动的N-S方程与描述电磁感应的麦克斯韦方程组联合求解。液态金属在强磁场中受到的洛仑兹力以体积力的形式作用于金属流体,不可压缩稳态流动的磁流体方程组无量纲形式为
(1)
(2)
(3)
(4)
式中:u——速度;
p——压力;
B——磁感应强度;
J——电流密度;
T——温度。
其中方程(1)为不可压缩流体力学连续性方程,方程(2)为流体力学动量方程,洛仑兹力对液态金属流动的影响以源项的形式体现在方程中,方程(3)为电势泊松方程,方程(4)为流体力学能量守恒方程,其中源项代表聚变反应过程中在矩形管道沉积的核热。
假设L为流道的特征长度, 为液态金属的动力学粘性系数,cp为比热容, 为液态金属的热导率,则方程中各项无量纲参数的定义为:雷诺数 ,哈特曼数 ,埃克特数 ,贝克莱数 ,相互作用参数 。
2.2. 数值方法
由于矩形流道中液态金属的流动处于稳态,对其求解可以分两步进行。首先,采用相容守恒格式与投影算法求解磁流体动力学方程 [5] ,得到流场中的速度分布,然后采用有限体积法求解流道中的能量方程,计算得出反映流道中传热情况的温度场分布。
对控制方程求解的数值模型采用非均匀结构化同位网格离散。如图1所示,将速度 ,压力p,电势 和温度T储存在格点中心。为保证电流守恒,将电流密度 储存在网格面元中心。因为液态金属边界层处电流密度很大,需要对边界层网格进行加密,一般将垂直与磁场的哈特曼层内划分为7个网格,平行于磁场的侧层划分为9个网格。
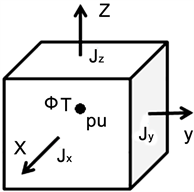
Figure 1. Structural sketch of discrete grid
图1. 离散网格结构示意图
在得到速度场分布的基础上,将能量守恒方程(4)采用有限体积法进行离散:
(5)
采用隐式方法对方程中的时间项和扩散项进行离散:
(6)
(7)
能量方程中的对流项采用二次迎风差值(QUICK)格式进行离散,并采用延迟修正的方法求解。该方法中低阶格式采用一阶迎风格式,并将高阶格式与低阶格式的差作为下一步迭代求解的源项。由于流道中液态金属沿x方向流动,对流项与源项的离散格式分别表示如下:
(8)
(9)
在以上离散格式中,x,y,z表示网格中心点的坐标,uf表示网格面元中心速度。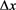 ,
,
分别表示沿笛卡尔坐标轴的网格长度。
表示聚变反应高能中子沉积在包层流道中的核热功率密度,数值为20 Mw/m3。
,
,
分别表示沿笛卡尔坐标轴的网格长度。
表示聚变反应高能中子沉积在包层流道中的核热功率密度,数值为20 Mw/m3。
离散后的能量方程采用交替方向隐式法与追赶法求解,并添加松弛因子避免求解过程发散。为加快求解的收敛过程,在能量方程求解过程中采用了块修正方法,在进行块修正值计算时,在每一个方向作一次块修正的计算后就对迭代的值进行一次修正,并以改进了的值去开始另一方向的块修正值计算。
2.3. 边界条件
图2为国际热核聚变实验堆(ITER)装置中真空室内部结构示意图。从图中可以看出,聚变堆包层被连接固定于真空室中,真空室处于低温恒温器的内部 [7] ,是一个密封的环形不锈钢容器。由于真空室与包层之间通过辐射方式传递的热量远小于聚变反应高能中子在包层中沉积的核热,因此在数值模拟过程中没有考虑聚变堆包层与真空室之间的热量交换。
Figure 2. Internal structure of ITER vacuum vessel
图2. ITER真空室内部结构示意图
在包层矩形流道壁面上应用绝热边界条件:
(10)
根据聚变堆包层中常用液态金属铅锂的工作温度,将矩形流道的入口温度设置为523, 。矩形流道的出口温度满足连续性条件, 。方程迭代求解的收敛标准是, 。求解过程中, 小于 。
3. 结果与讨论
为验证数值模拟程序,矩形流道中流体区域的无量纲尺寸设置为 ,并建立了液态金属在矩形流道中的充分发展MHD层流模型。数值模拟程序代码使用Fortran90语言编写,由Intel Visual Fortran Composer XE 2013编译器编译运行。为加快运行速度,程序设计过程中采用了共享存储并行编程技术OpenMP,在Intel (R)计算机平台上利用8线程进行并行计算。为确定计算所用网格的网格数量与计算结果之间的无关联性,程序分别将流体区域划分为 、 和 个网格进行无关性验证。由于流体速度与流动和传热现象直接相关,因此取管道中间x = 3.0,z = 0处水平方向上的速度分布进行计算,计算结果如图3所示。从图中可以看出,当网格数量从33万增长到45万时,计算结果的变化很小,因此数值模拟程序的计算过程具有网格无关性。由于在MHD流动计算中Shercliff算例和Hunt算例有理论解,通常将其作为MHD数值模拟程序的标准算例。

Figure 3. Grid independence verification result
图3. 网格无关性验证结果图
3.1. 速度分布
在Shercliff算例中,流体的无量纲电导率为1,流道壁的无量纲电导率为0。将流动区域划分为 个网格。数值模拟程序分别计算了Ha = 300,Re = 10、Ha = 500,Re = 10与Ha = 1000,Re = 500三种情况下的速度分布。在流道x = 3.0处的速度分布如图4所示。从图中可以看出,数值解和理论解非常接近。表1为算例中的流量与压力梯度的计算结果,可以看出,Shercliff算例中压力梯度的最大误差为6%,流量的最大误差为0.1%。
 (a)
(a) 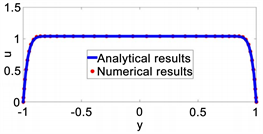 (b)
(b)
Figure 4. Shercliff’s case results (Ha = 500, Re = 10); (a) Three dimensional velocity distribution of a cross section at x = 3.0; (b) Compare between numerical results and analytical results
图4. Shercliff’s算例计算结果(Ha = 500,Re = 10);(a) x = 3.0处的速度分布图;(b) 数值解与理论解的对比
在Hunt算例中,矩形流道平行于外部磁场的侧壁为绝缘壁,垂直于磁场的哈特曼壁的无量纲电导率为0.05。数值模拟程序分别计算了Ha = 500,Re = 10与Ha = 1000,Re = 500两种情况下的速度分布情况,并在图5中表示出矩形流道x = 3处的速度分布。从图中可以看出,在流道侧壁附近出现了很强的剪切流动,数值解与理论解也符合得很好。表1中流量与压力梯度的计算结果表示,算例中压力梯度的最大误差为4%,流量的最大误差为0.1%。
 (a)
(a)  (b)
(b)
Figure 5. Hunt’s case results (Ha = 1000, Re = 500); (a) Three dimensional velocity distribution of a cross section at x = 3.0; (b) Compare between numerical results and analytical results
图5. Hunt算例计算结果(Ha = 1000,Re = 500);(a) x = 3.0处的速度分布图;(b) 数值解与理论解的对比
Table 1. Pressure gradient and flow rate for Shercliff’s case and Hunt’s case
表1. Shercliff算例与Hunt算例中的压力梯度与流量
3.2. 温度分布
在数值模拟程序得到的速度分布的基础上,通过求解能量守恒方程得到了流道中的温度分布情况。根据能量守恒关系,当流道中温度分布达到稳态时,沉积的核热应等于从流道中净流出的热量,从而有如下的守恒关系成立:
(11)
式中: ——流道中沉积的核热;
——流道体积;
——密度;
cp——比热容;
Tin——入口温度;
Tout——出口温度。
从能量守恒的角度,数值模拟程序的计算误差可以表示为:
(12)
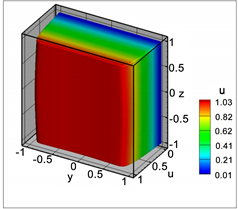
图6为计算程序模拟的Ha = 1000,Re = 500时Hunt算例的温度分布情况。流道中的流体为液态PbLi,入口的温度设定为523 K。流道中沉积的核热为20 Mw/m3,与中子在流道中沉积的核热功率平衡相比,数值计算结果的误差为3.2%。
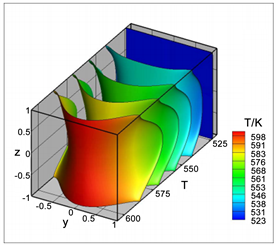
Figure 6. Temperature distribution of Hunt case: Ha = 1000, Re = 500
图6. Hunt算例温度分布图(Ha = 1000,Re = 500)
4. 结论
提出了计算聚变堆液态包层增殖区不可压缩液态金属流动时传热分布的方法。该方法首先利用四步投影法计算出流场中的速度分布,将能量方程使用有限体积法进行离散,其中扩散项直接差分,对流项采用二次迎风差值格式离散。采用交替方向隐式法与追赶法求解能量方程得到了流道中的温度分布。并采用标准算例和能量守恒的方法验证了数值模拟结果的可靠性,为研究聚变堆包层中液态金属的传热分布提供了参考。
基金项目
本论文中的研究工作是在国家磁约束核聚变能发展研究专项“磁约束聚变堆内部件关键技术问题研究” (项目编号:2013GB113000)和国家自然科学基金项目“聚变堆强磁场与高核热梯度下包层液态铅锂载氚热磁流体MHD流动氚传输机理研究” (项目编号:51576208)的资助下开展的。
文章引用
韩佳佳,汪卫华. 聚变堆液态金属包层MHD流动和传热数值模拟程序开发与验证
Development and Validation of Numerical Simulation Program for MHD Flow and Heat Transfer in Liquid Metal Blanket of Fusion Reactor[J]. 核科学与技术, 2019, 07(03): 83-90. https://doi.org/10.12677/NST.2019.73012
参考文献
- 1. Abdou, M.A., Morley, N.B. and Ying, A.Y. (2005) Overview of Fusion Blanket R&D in the US over the Last Decade. Nuclear Engineering and Technology, 37, 401-422.
- 2. Wong, C.P.C., Salavy, J.F., Kim, Y., Kirillov, I., Rajendra Kumar, E., Morley, N.B., et al. (2008) Overview of Liquid Metal TBM Concepts and Programs. Fusion Engineering and Design, 83, 850-857. https://doi.org/10.1016/j.fusengdes.2008.06.040
- 3. Shercliff, J.A. (1953) Steady Motion of Conducting Fluids in Pipes under Transverse Magnetic Fields. Proceedings of the Cambridge Philosophical Society, 49, 136-144. https://doi.org/10.1017/S0305004100028139
- 4. Hunt, J.C.R. (1965) Magnetohydrodynamic Flow in Rectangular Ducts. Journal of Fluid Mechanics, 21, 577-590. https://doi.org/10.1017/S0022112065000344
- 5. Ni, M.-J., Munipalli, R., Morley, N.B., Huang, P. and Abdou, M.A. (2007) A Current Density Conservative Scheme for Incompressible MHD Flows at a Low Magnetic Reynolds Number. Part I: On a Rectangular Collocated Grid System. Journal of Computational Physics, 227, 174-204. https://doi.org/10.1016/j.jcp.2007.07.025
- 6. Smolentsev, S., Morley, N.B., et al. (2008) MHD and Heat Transfer Considerations for the US DCLL Blanket for DEMO and ITER TBM. Fusion Engineering and Design, 83, 1788-1791. https://doi.org/10.1016/j.fusengdes.2008.04.002
- 7. 袁保山, 姜韶风, 陆志鸿. 托卡马克装置工程基础[M]. 北京: 原子能出版社, 2011: 381-387.
NOTES
*通讯作者。
