Modeling and Simulation
Vol.
11
No.
03
(
2022
), Article ID:
51530
,
16
pages
10.12677/MOS.2022.113073
M-CVaR准则下具有风险偏好的双渠道供应链决策分析
吴福田,党亚峥*,白妮蔓
上海理工大学管理学院,上海
收稿日期:2022年4月17日;录用日期:2022年5月16日;发布日期:2022年5月23日

摘要
本文针对供应商为风险中性,零售商具有风险偏好的双渠道销售的两级供应链系统。在条件风险值(CVaR)准则基础上,创造性的提出了利用均值条件风险价值(M-CVaR)度量风险偏好,融合风险厌恶度和悲观系数建立了基于M-CVaR决策准则的双渠道销售供应链模型。最后讨论零售商的不同风险偏好度对供应链最优决策的影响,并通过数值分析验证了模型的可行性。研究表明:1) M-CVaR决策准则比条件风险值准则更能完整度量决策者的风险偏好度;2) 具有风险偏好的双渠道供应链可通过均值条件风险价值决策准则寻找最优决策。
关键词
M-CVaR准则,双渠道供应链,Nash博弈,风险偏好

Decision Analysis of Dual-Channel Supply Chain with Risk Preference under M-CVaR Criterion
Futian Wu, Yazheng Dang*, Niman Bai
School of Management, University of Shanghai for Science and Technology, Shanghai
Received: Apr. 17th, 2022; accepted: May 16th, 2022; published: May 23rd, 2022

ABSTRACT
This paper aims at the two-level supply chain system of dual-channel sales in which the supplier is risk-neutral and the retailer has risk preference. Based on the conditional value at risk (CVaR) criterion, this paper creatively puts forward the use of mean conditional value at risk (m-CVaR) to measure risk preference, integrates risk aversion and pessimism coefficient, and establishes a dual-channel sales supply chain model based on m-CVaR decision criterion. Finally, the influence of retailers’ different risk preference on the optimal decision-making of supply chain is discussed, and the feasibility of the model is verified by numerical analysis. The research shows that: 1) m-CVaR decision criterion can more completely measure the risk preference of decision-makers than conditional value at risk criterion; 2) The dual-channel supply chain with risk preference can find the optimal decision through the mean conditional value at risk decision criterion.
Keywords:M-CVaR Criterion, Dual-Channel Supply Chain, Nash Game, Risk Preference

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着移动支付和互联网的高速发展,加快了电子商务的发展,双渠道供应链管理模式也逐渐被企业认可。因此双渠道供应链的协调问题,特别是面对不同风险偏好的决策问题成为研究热点。
随着移动支付和互联网的高速发展,加快了电子商务的发展,双渠道供应链管理模式也逐渐被企业认可。因此双渠道供应链的协调问题,特别是面对不同风险偏好的决策问题成为研究热点。
近年来,国内外学者逐渐加强对决策者具有风险偏好的研究。处于不同情况中,决策者面临风险时有三种表现,分别是风险中性、风险厌恶和风险喜好。但是目前大多数文献仅针对风险中性、风险厌恶的风险偏好进行研究。王虹于2010年,针对具有风险规避特征的供应商和零售商组成的双渠道供应链,分析非竞争环境下双渠道供应链中产品在不同渠道的最优定价 [1]。曹文彬等在2014年,讨论了在随机的市场需求条件下,零售商风险规避对供应商双渠道选择的影响 [2]。许民利等在2016年,运用CVaR准则建立双渠道供应链定价决策模型,讨论了风险偏好对双渠道供应链决策的影响 [3]。赵静于2016年,考虑了包含一个风险厌恶的供应商和一个风险中性的零售商组成的双渠道供应链,运用博弈论和CVaR准则,分析了供应商风险厌恶度对供应商和零售商最优决策的影响 [4]。王聪等在2017年,分析了在市场需求信息不确定条件下,零售商与供应商共享市场预测信息及零售商风险偏好对供应链成员决策及利润的影响 [5]。方青于2018年,讨论了一个供应商和一个风险规避型零售商主导的双渠道供应链的定价策略问题 [6]。郭金森于2018年,研究了在对称信息框架下,基于风险厌恶零售商的双渠道闭环供应链运作策略 [7]。史思雨等在2021年,研究了风险规避型零售商资金约束下双渠道闭环供应链的定价决策问题 [8]。于丽萍等在2021年,研究了零售商风险规避下差异化渠道的三层供应链协调问题 [9]。谭乐平等在2021年,研究了在零售商资金约束下,基于CVaR准则讨论风险规避的供应商和零售商组成的双渠道供应链最优决策问题 [10]。Jammernegg等在2009年,经过实证调查,得出供应链成员的风险偏好可分为风险中性、风险喜好、风险厌恶三种类型,并在CVaR基础上提出能够统一度量以上三种风险偏好水平的M-CVaR [11]。现有的一些文献绝大部分是运用均值–条件风险价值统一度量决策者的风险偏好,以此来分析供应链决策问题。例如Wei等在2010年,讨论了在均值–方差框架下利用利润共享契约协调供应链的问题 [12]。钟昌宝等在2016年,运用均值–条件风险价值统一度量决策者的风险喜好、中性及厌恶水平,并据此研究考虑决策者风险偏好水平的供应链收益共享契约协调问题 [13]。郭泉等在2017年,研究了在随机需求下基于M-CVaR的仓储服务定价决策 [14]。蔡鑫等在2021年,讨论了供应商面临生产资金约束的情况,在需求随机条件下研究了由一个风险中性零售商和一个具有风险偏好的供应商组成的二级供应链的协调问题 [15]。
以上文献 [1] - [10] 将供应链成员的风险偏好融入传统供应链契约,以供应商或零售商为风险中性或风险厌恶为前提,在一定程度上使契约更加符合实际需求,但是没有考虑现实中存在风险喜好型的供应链成员。文献 [11] [12] [13] [14] [15] 即使运用M-CVaR度量风险偏好度。但是基本上都是运用在单渠道供应链上。现有文献缺少对存在风险偏好的双渠道供应链的研究。本文借鉴文献 [10] 和 [13] 的研究方法,突破性地研究风险偏好和双渠道供应链决策。
本文具体针对双渠道销售的两级供应链系统,其中供应商为风险中性,零售商具有风险偏好。本文结构安排如下:首先运用博弈论和CVaR准则,建立基于CVaR度量的零售商风险偏好博弈模型,讨论零售商的不同风险偏好度对双渠道供应链系统最优决策的影响;然后运用M-CVaR决策准则度量供应链成员风险偏好度。建立基于M-CVaR决策准则的双渠道销售供应链模型,分别讨论零售商的风险厌恶度和零售商的悲观系数对双渠道供应链系统最优决策的影响;最后对比在CVaR和M-CVaR度量供应链成员风险偏好度时,零售商悲观系数对供应链决策的影响。本文提出的运用M-CVaR度量风险偏好的双渠道供应链的模型,丰富了研究风险偏好的供应链文献。
2. 问题描述及假设
本文考虑包含一个供应商和零售商组成的二级供应链,供应商以单位成本c生产某一种产品,通过两种渠道进行销售:一种是网络直销渠道且直销生产量为 ,即供应商以单位直销价 直接销售给客户;第二种是传统零售渠道,即以单位批发价格w销售给零售商 ,零售商订购量 ,再以单位零售价格 销售给客户。
假设零售渠道和直销渠道的需求函数分别为:
(1)
(2)
式中a表示市场基础; 表示直销渠道所占市场份额比例; 表示零售渠道所占市场份额比例; 和 分别表示直销渠道对直销价格和零售渠道对零售价格的自身敏感系数; 表示直销渠道对零售价格和零售渠道对直销价格的交叉敏感系数 。随机变量 分别表示直销渠道风险和零售渠道风
险,假设定义在 上, 的分布函数和密度函数分别为 和 ,且 ,,由文献 [16] 可知 的失败率函数 ,对于 , -失败率函数 。令 表示期望需求, 。
假设此产品是短生命周期或季节性的产品,销售时段过后,供应商和零售商均以单位价格s进行促销,因此 。对于此类产品,文献 [17] 指出不考虑残值和缺货成本是合理的。因此本文假设如下:
1)供应商和零售商都是各自最求自己最大的利润为目标进行决策;
2)不考虑零售商的销售成本和库存成本、供应商的销售成本和库存成本;
3) 供应商为风险中性,零售商具有风险偏好,风险偏好影响决策行为。
基于以上假设零售商和供应商的收益函数。
零售商收益函数:
(3)
供应商收益函数:
(4)
考虑供应商为风险中性,那么供应商的期望利润:
(5)
式中 为直销渠道的期望需求函数 的简写。
CVaR度量了低于 分位数的收益平均值,而忽略了其收益会超出的那一部分,所以CVaR只能度量风险厌恶或者中性的情况。
置信水平 下零售商的 -CVaR函数为:
(6)
表示零售商的风险厌恶度, 越小表示零售商对风险越厌恶,当 时零售商为风险中性。 为分位数,令
(7)
(8)
3. 模型建立及求解分析
本节基于上节的假设条件下以及供应链的收益函数,先求出供应商和零售商的反应函数,然后建立基于CVaR度量的零售商风险偏好的博弈模型,最后对模型进行分析。
3.1. 供应商的反应函数
分析供应商的收益期望函数和直销渠道的需求风险失败率,可以得到定理1。
定理1当直销渠道的需求风险失败率 时,供应商的期望利润 是关于 的联合凹函数。
证明由(5)式, 关于 的一阶偏导数分别为:
(9)
(10)
关于 的海瑟矩阵为:
,
式中,
,
,
,
。
其顺序主子式 ,。易证当 时, ,海瑟矩阵此时负定。因此,供应商的期望利润 是关于 的联合凹函数。证毕。
由定理1可知,供应商的期望利润 关于 的二阶导数小于0,所以供应商的期望利润函数存在唯一的最大值。令其一阶偏导等于0。
定理2在给定零售价 和零售订购量 时,当直销渠道需求风险函数 时,存在唯一均衡 , 满足以下条件:
(11)
(12)
性质1最优直销价和直销渠道生产量随着零售价的增加而增加,即: 。
证明(11)式两边对 求导,可得:
(13)
由定理1可知 ,所以,
因此 。
(12)式两边对 求偏导,可得:
(14)
证毕。
3.2. 零售商的反应函数
本小节运用CVaR准则度量零售商风险偏好,在求得零售商利润在置信度 时的CVaR函数,经过证明得到定理3。如下:
定理3存在 ,使得
证明由(7)式得
其中 ,。
1) 当 时, ,故 是关于v的单调递增函数;
2) 时,
,
。
,故 是关于v的凹函数
3) 当 时,
。
因 ,所以 是关于v的单调递减函数。
综上(1)~(3)可以得到 在区间上 取得最大值,并且最大值点为
(15)
证毕。
由定理3,可知当 时,
,
因,此时 ,所以零售商的最优订购量不会落在此区间。
当 时,
(16)
式中 为零售渠道的期望需求函数 的简写。
定理4当零售渠道需求风险的 -失败率 时,零售商的 是关于 的联合凹函数。
证明 是关于 的海瑟矩阵为:
。
同定理1的证明。易证当 时,海瑟矩阵负定,从而证明 是关于 的联合凹函数。证毕。
定理5再给定的直销渠道售价 和直销渠道生产量 ,当直销渠道需求风险函数 时,存在均衡零售价 和零售商订购量 满足以下条件:
(17)
(18)
性质2最优零售价和零售商订购量随着直销价的增加而增加,即: 。
3.3. 模型最优解及分析
由2.1和2.2得到的供应商和零售商的反应函数,可建立基于CVaR度量的零售商风险偏好博弈模型。供应商和零售商同时进行Nash博弈,他们同时进行决策。供应商决策直销渠道价格和直销渠道生产量,零售商决定零售价格和订购量。建立模型如下
(19)
联立(11)、(12)、(17)、(18)式,既可以得到该博弈模型的最优直销价 ,直销渠道生产量 。零售价 ,零售商订购量 ,通过分析可以得到以下性质:
性质3 ,,,。
证明(11)式和(17)式两边分别对 求偏导可得:
(20)
(21)
其中 ,,
,
联立(20)和(21)式可以得到, ,。由定理2的条件 可知, 。
由定理4的条件可知 ,同理可证 。又 ,故 。可得, ,。
(12)式两边对 求偏导,结合(11)式可得 ;(18)式两边对 求偏导,结合(17)式可得 。证毕。
(11),(12)式和(17),(18)式,分别对参数 和 求偏导,得到参数 和 对最优直销价,最优零售价,最优直销生产量,最优零售订购量的影响,可得性质4
性质4
,,, ;
,,, ;
,,, ;
性质4 1) 表明零售价、直销价、零售商订购量和直销渠道生产量都是交叉敏感系数的增加而增加;2) 表明零售价,直销价,零售商订购量和直销渠道生产量都是直销价格敏感系数的增加而减少;3) 表明零售价,直销价,零售商订购量和直销渠道生产量都是零售价格敏感系数的增加而减少。
4. 零售商基于M-CVaR度量风险偏好的模型
由上节得得到的基于CVaR度量的零售商风险偏好博弈模型,然后本节在此基础上,建立了基于均值条件风险价值(M-CVaR)决策准则的双渠道销售供应链模型。
4.1. M-CVaR基础模型
由文献 [13] 可知零售商的M-CVaR基础模型为:
(22)
令: 。
其中为 为零售商的悲观系数, ,当 时,模型成为假设决策者为风险中性,以期望收益最大化为目标的传模型;当 时,决策者更看重收益高于分位数的部分,此时其为风险喜好;反之,当 时,决策者为风险厌恶,且当 时,决策者只看重收益低于分位数的部分,模型为假设决策者是风险厌恶的CVaR模型。
4.2. M-CVaR度量风险偏好的模型
根据零售商利润函数(3)式,可得零售商的期望利润:
,
可得,当 时,即 时,其中 表示零售商需求风险函数的 分位数。
当 时,
因此,
当 ,此时 ,不为凹函数,故最优解不在此区间。
以下只讨论 的情况,所以,
(23)
定理6当零售渠道需求的风险失败率 时, 是关于 的联合凹函数。
证明 关于 的海瑟矩阵为:
。
同定理1的证明,易证当 时,海瑟矩阵负定,故 是关于 的联合凹函数。
定理7再给定的直销渠道售价 和直销渠道生产量 ,当直销渠道需求风险函数
时,存在均衡零售价 和零售商订购量 满足以
(24)
(25)
性质5最优零售价和零售商订购量随着直销价的增加而增加,即: 。
联立(11)、(12)、(24)、(25)式,既可以得到该博弈模型的最优直销价 ,直销渠道生产量 。零售价 ,零售商订购量 ,通过对 的分析可以得性质6。
性质6最优直销价 ,直销渠道生产量 。零售价 ,零售商订购量 。均随着 的变化而变化。
5. 数值分析
5.1. CVaR模型分析
本节采用MATLAB数值分析CVaR模型中的风险偏好度对价格、订购量、利润的影响。参数赋值如下: ,,,,,,, 服从 上的均匀分布 。
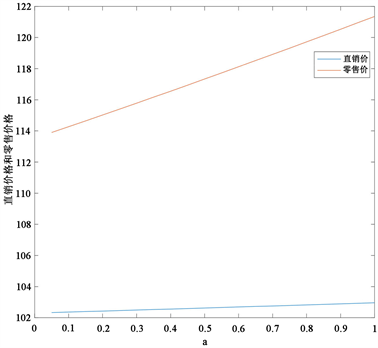
Figure 1. The impact of risk preference on optimal pricing
图1. 风险偏好度对最优定价的影响
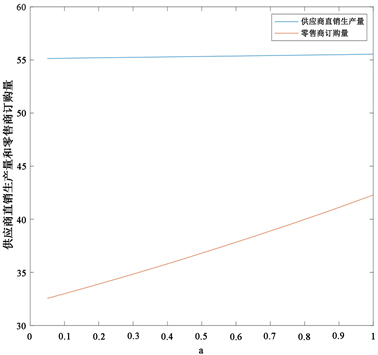
Figure 2. The effect of risk preference on order quantity
图2. 风险偏好度对订购量的影响
图1~3反映了考虑CVaR测度时,不同风险偏好度对最优定价、直销渠道生产量和零售商订购量、供应商期望利润和零售商CVaR值的影响。根据图1~3可知供应商最优直销价、生产量、利润和零售商最优零售价、订购量、CVaR值均随着零售商风险偏好度 的增大而增大。
5.2. M-CVaR模型分析
本节采用MATLAB数值分析分析M-CVaR模型中的风险偏好度和悲观系数对价格、订购量、利润的影响。参数赋值如下: ,,,,,,, 服从 上的均匀分布 。

Figure 3. The effect of risk preference on supplier expected profit and retailer CVaR
图 3. 风险偏好度对供应商期望利润和零售商CVaR值的影响
图4~9反映了考虑M-CVaR测度时,不同零售商风险偏好度和零售商悲观系数对最优定价、直销渠道生产量和零售商订购量、供应商期望利润和零售商M-CVaR值的影响。
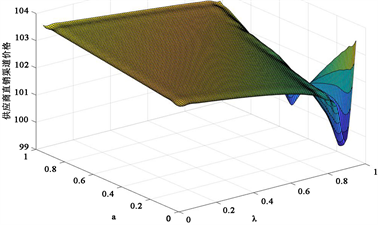
Figure 4. The impact of risk preference and pessimism coefficient on direct selling prices
图4. 风险偏好度和悲观系数对直销价格的影响
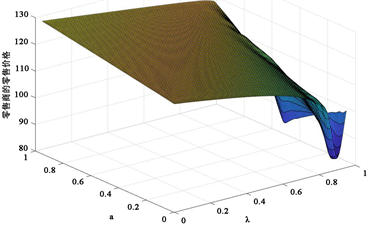
Figure 5. The impact of risk preference and pessimism coefficient on retail prices
图5. 风险偏好度和悲观系数对零售价格的影响
图4展示了,当零售商风险偏好度一定时,供应商直销渠道价格随着当零售商的悲观系数增大而先减小后增大。图5展示了,当零售商风险偏好度一定时,零售商零售价格随着零售商悲观系数的增大而先减小后增大的不稳定现象。
从图6~8中可以看出供应商直销渠道生产量、零售商订购量和供应商期望利润均随着零售商风险偏好度的减小而减小,零售商悲观系数的增大而减小。图9展示了,零售商风险偏好度一定时,零售商的M-CVaR值随着零售商的悲观系数的增大而先减小后增大。
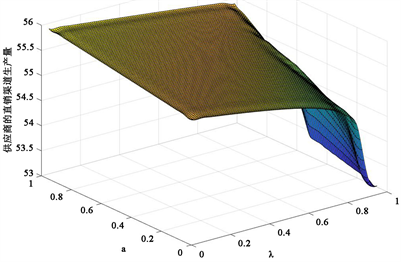
Figure 6. The impact of risk preference and pessimism coefficient on direct selling production
图6. 风险偏好度和悲观系数对直销生产量的影响
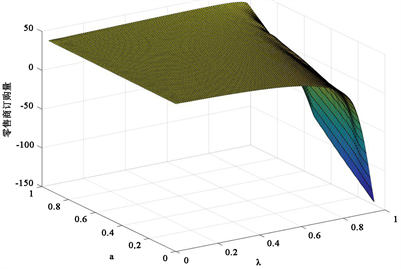
Figure 7. The effect of risk preference and pessimism coefficient on retailer’s order quantity
图7. 风险偏好度和悲观系数对零售商订购量的影响
5.3. CVaR和M-CVaR模型仿真对比
本节采用MATLAB数值分析分析两种模型中的风险偏好度和悲观系数供应链利润的影响。参数赋值如下: ,,,,,,, 服从 上的均匀分布 。
图10、图11展示了,在不同零售商悲观系数下,零售商风险偏好度对供应商期望利润和零售商CVaR值、M-CVaR值的影响。CVaR模型度量风险偏好度时忽略了悲观系数,而M-CVaR模型却能弥补这个
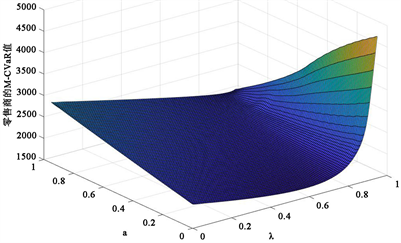
Figure 8. The effect of risk preference and pessimism coefficient on retailers’ M-CVaR value
图8. 风险偏好度和悲观系数对零售商的M-CVaR值的影响
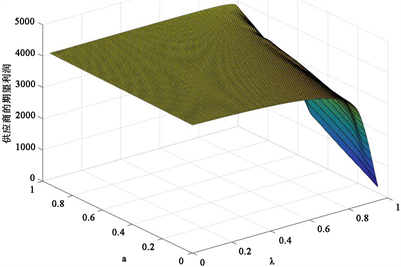
Figure 9. Impact of risk preference and pessimism coefficient on supplier expected profit
图9. 风险偏好度和悲观系数对供应商期望利润的影响
缺陷。从图10可以看出在M-CVaR模型度量时在 时供应商的期望利润要优于 ,且也优于CVaR模型度量时的供应商期望利润。从图11可以看出在M-CVaR模型度量风险偏好度时在 时零售商M-CVaR值要优于 ,且也优于CVaR模型度量时的零售商CVaR值。这表明在M-CVaR模型度量风险偏好度时,该模型的零售商悲观系数 值对供应链的收益起到决定性的作用。也可根据零售商悲观系数 值预测供应链的收益情况。
6. 结论及展望
本文研究了在随机市场需求情况下,风险中性的供应商和风险偏好的零售商组成的双渠道供应链。在零售商具有风险偏好的情况下,首先建立了CVaR准则下的决策模型,分析零售商的风险厌恶度对供应链决策的影响。得到随着零售商的风险厌恶度 与供应商和零售商的最优定价、直销渠道生产量和零售商订购量、供应商期望利润和零售商的CVaR值成正比。在此基础上建立了M-CVaR准则下的决策模型,分析了零售商的风险厌恶度 和悲观系数 对供应链决策的影响。研究表明1) 均值条件风险价值(M-CVaR)决策准则比条件风险值(CVaR)准则更能完整度量决策者的风险偏好度;2) 利用均值条件风险价值(M-CVaR)决策准则可以帮助供应链成员获取更大的利润。根据以上分析可以看出,在双渠道供应链
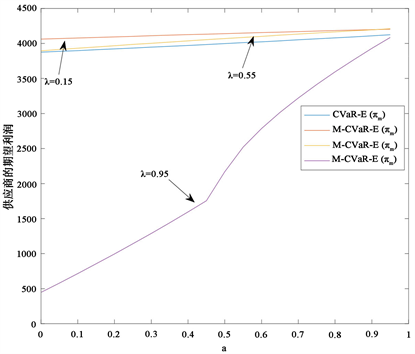
Figure 10. The impact of risk preference on suppliers’ expected profits
图10. 风险偏好度对供应商期望利润的影响
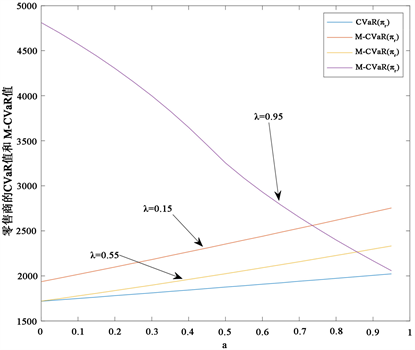
Figure 11. The effect of risk preference on retailers’ CVaR and M-CVaR
图11. 风险偏好度对零售商CVaR值和M-CVaR值的影响
决策中,供应链成员的最优定价、订购量和收益均受风险偏好的影响。因此在研究供应链决策问题时,并不能单纯假设风险中性和风险厌恶,风险喜好应该也考虑进去。同时在实际决策中,供应商应该考虑零售商的风险偏好度,结合自身的情况作出最优决策。
虽然本文考虑了零售商的风险偏好水平,但是还是假设供应商的风险偏好为中性,现实中还是存在供应商具有风险偏好行为的。因此考虑双方风险偏好的双渠道供应链的决策研究是下一步的研究方向。
文章引用
吴福田,党亚峥,白妮蔓. M-CVaR准则下具有风险偏好的双渠道供应链决策分析
Decision Analysis of Dual-Channel Supply Chain with Risk Preference under M-CVaR Criterion[J]. 建模与仿真, 2022, 11(03): 781-796. https://doi.org/10.12677/MOS.2022.113073
参考文献
- 1. 王虹, 周晶. 竞争和风险规避对双渠道供应链决策的影响[J]. 管理科学, 2010, 23(1): 10-17.
- 2. 曹文彬, 左慧慧. 零售商风险规避对供应商双渠道选择的影响[J]. 商业研究, 2014(6): 20-26.
- 3. 许民利, 聂晓哲, 简惠云. 不同风险偏好下双渠道供应链定价决策[J]. 控制与决策, 2016, 31(1): 91-98.
- 4. 赵静, 朱昆. CVaR准则下双渠道供应链决策与博弈模型[J]. 天津工业大学学报, 2016, 35(1): 75-82.
- 5. 王聪, 杨德礼, 程兴群. 考虑零售商风险偏好的双渠道供应链信息共享研究[J]. 工业工程与管理, 2017, 22(2): 83-88+96.
- 6. 方青, 任亮, 张子刚, 邵嫄. 风险规避型零售商双渠道供应链定价策略研究[J]. 预测, 2018, 37(1): 68-74.
- 7. 郭金森, 周永务, 任鸣鸣, 海本禄. 基于风险厌恶零售商的双渠道闭环供应链运作策略[J]. 运筹与管理, 2018, 27(8): 32-40.
- 8. 史思雨, 孙静春, 邓飞. 风险规避型零售商资金约束下双渠道闭环供应链的定价决策[J]. 运筹与管理, 2021, 30(4): 1-9.
- 9. 于丽萍, 李莉杰. 零售商风险规避下差异化渠道的三层供应链协调[J]. 东北大学学报(自然科学版), 2021, 42(2): 282-289.
- 10. 谭乐平, 宋平, 杨琦峰. 风险规避型双渠道供应链的融资和定价决策[J]. 计算机工程与应用, 2021, 57(7): 237-250.
- 11. Jammernegg, W. and Kischka, P. (2009) Rish Preferences and Robust Inventory Decisions. International Journal of Production Economics, 118, 269-274. https://doi.org/10.1016/j.ijpe.2008.08.023
- 12. Wei, Y. and Choi, T.M. (2010) Mean-Variance Analysis of Supply Chains under Wholesale Piecing and Profit Sharing Schemes. European Journal of Operational Research, 204, 255-262. https://doi.org/10.1016/j.ejor.2009.10.016
- 13. 钟昌宝, 丁彦学, 张宏如. 基于M-CVaR的供应链收益共享契约协调研究[J]. 运筹与管理, 2016, 25(6): 53-58.
- 14. 郭泉. 随机需求下基于M-CVaR的仓储服务定价决策研究[J]. 长沙航空职业技术学院学报, 2017, 17(3): 89-92.
- 15. 蔡鑫, 郑尊信. 基于M-CVaR和生产资金约束的供应链协调研究[J]. 运筹与管理, 2021, 30(4): 61-68.
- 16. Chen, X., Xu, M.H. and Zhang, G. (2009) A Risk-Averse Newsvendor Model under CVaR Decision Criterion. Operations Research, 57, 1040-1054. https://doi.org/10.1287/opre.1080.0603
- 17. Wang, Y., Jiang, L. and Shen, Z.-J. (2004) Channel Performance under Consignment Contract with Revenue Sharing. Management Science, 50, 34-47. https://doi.org/10.1287/mnsc.1030.0168
NOTES
*通讯作者。