Advances in Applied Mathematics
Vol.
08
No.
04
(
2019
), Article ID:
29994
,
12
pages
10.12677/AAM.2019.84093
Research on the Replication of the Option of Random Walk Market and Deducing Some Formulas
Dawei Tang, Zhizhuo Cai
Zhejiang Zhuosheng Xianghong Asset Management Co., Ltd., Jiaxing Zhejiang

Received: Apr. 6th, 2019; accepted: Apr. 21st, 2019; published: Apr. 28th, 2019

ABSTRACT
First, this paper deduces the option pricing formula of random walks, and then proposes three propositions and proves them separately. Proposition 1 explains the principle of option replication from a new perspective. Proposition 2 finds two inequalities and gives the upper and lower bounds of the cumulative function of the standard normal distribution. Combining Proposition 2 and Proposition 3, four elementary functions that approximate the cumulative function of the standard normal distribution are found. The second function has the highest precision: the maximum absolute error is 0.0000406.
Keywords:Option, Random Walk, Inequality, Approximation, Error
随机游走行情期权复制的研究并推导出若干 公式
汤大伟,蔡之卓
浙江卓盛祥鸿资产管理有限公司,浙江 嘉兴

收稿日期:2019年4月6日;录用日期:2019年4月21日;发布日期:2019年4月28日

摘 要
首先,本文推导出随机游走行情的期权定价公式,然后提出三个命题并分别证明。命题一从新的角度阐述期权复制原理。命题二发现两个不等式,给出了标准正态分布累积函数的上下界。结合命题二和命题三发现了四个逼近标准正态分布累积函数的初等函数,第二个函数的精度最高:最大绝对误差是0.0000406。
关键词 :期权,随机游走,不等式,近似,误差

Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
Black-Scholes期权定价模型不太适用零和博弈市场如期货市场。且BS公式在计算到期时间短的期权价格时偏差较大。金融市场长线行情或可预测但短线行情往往非常近似随机游走行情。所以本文从随机游走行情推导期权定价公式并提出三个命题,给出证明并推导出若干公式。
2. 正文
记 为标准正态分布概率密度函数:
[1]
N为标准正态分布变量的累积概率分布函数:
[1]
设标的资产的行情为随机游走行情,该随机游走行情单位时间涨跌幅度均值为0,标准差为 (不同于BS公式里的标准差),那么T个单位时间的涨跌幅度的均值为0,标准差为 。
设当前价格为S,期权执行价格为K,则到期时间为T个单位时间的期权价格C的表达式为:
,
易验证 的导数为 ,所以 的一个原函数是 ,
那么易解得:
又 ,所以C亦可写成:
标的资产价格上涨dS时,期权价值上涨dC,所以最佳对冲比例为:
将S看作自变量,对C求导后并化简得:
当 ,此时该标的资产单位时间涨跌幅度均值为0,标准差为1,当前价格为0,
下文是在 的情况下进行计算和证明,不影响所提出的结论,不再另作说明。
命题一:
随机游走行情中,卖出一份看涨期权获得期权费 同时买入 份标的资产,到期时的损益与一份看涨期权到期时的价值最接近。即买入 份标的资产到期时的损益与买入一份看涨期权到期时的损益(期权到期时的价值减去期权费 )最接近,也就表明通过买卖标的资产可以复制期权。
证明:设持有 份标的资产、到期时标的资产价格为 ,因已设当前价格S = 0,所以到期时的资产损益为 (x为负数时表示亏损)。
到期时若 小于等于K,那么到期时的期权价值为0。期权费 加上到期时资产损益 与期权价值之差为:
到期时若 大于K,那么到期时的期权价值为 。期权费 加上到期时资产损益 与期权价值之差为:
应用最小二乘法,
令
命题中所有可能的值最接近0指的是最小化 。
当 的导数(M是自变量) 时, 最小。
为方差的定义,因方差为1,所以 ,上式整理为:
所以, 。
下面证 ;
移项得,只需证: ;
左右两侧分别对K求导:
左侧式子导数为: ,
即 ;
即 ;
右侧式子导数为: ;
证明了左侧式子的导数 = 右侧式子的导数。
那么由此可知:左侧式子 = 右侧式子 + 一个常数。
且当K = 时,右侧式子是方差的定义,因方差是1,所以右侧是1,左侧将K = 带入,也是1,说明所加常数为0, 成立,所以 ,命题得证。
在证明命题一的过程中,我们得到一个很简洁的等式:
等式一:
为了引出命题二,先考虑两个方程。
考虑如下两个情形:
情形1 (设标的资产到期价格为 ):
卖出一份期权获得期权费C,同时买入 份标的资产,期权到期时再根据到期行情的价格支付期权买方所应得金额后,若要求此时的盈亏值在到期行情大于等于S的情况下(即 ),期望值为0,求解 。
即 满足如下式子:
再结合 以及 。
求解得:
情形2 (设标的资产到期价格为 ):
卖出一份期权获得期权费C,同时买入 份标的资产,期权到期时再根据到期行情的价格支付期权买方所应得金额后,若要求此时的盈亏值在到期行情大于等于 的情况下(即 ),期望值为0,求解 。
即 满足如下式子:
再结合 以及 。
求解得:
命题二:
证明:为了证明时论述方便,这里将自变量 换为 ,同时结合 。
将命题二等价转换为以下两个不等式:
不等式一:
不等式二:
不等式一的证明:
不等式一的右侧式子中有一个分母是2x,此时用极限求x = 0时的值。
不等式一的右侧式子给出了 的一个下界初等函数,用这个下界函数减去 后的函数图如图1所示。

Figure 1. The lower bound function minus
图1. 下界函数减去
令
,
的函数图像即是图1。
当x = 0时,应用极限,显然 = 0,此时满足式子。当x > 0时,考察 的导数 的性质:导数 先小于0,接着,当 ,导数 ,又因 ,所以证明了 ,故该不等式成立。
不等式二的证明:
不等式二的右侧式子给出了 的一个上界初等函数,用这个上界函数减去 后的函数图如图2所示。
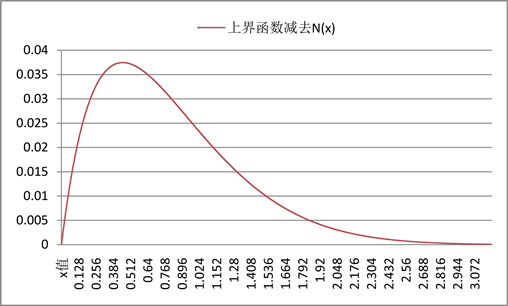
Figure 2. The upper bound function minus
图2. 上界函数减去
令 , 的函数图像即是图2。
当x = 0时,显然 ,即满足式子。当x > 0时,考察 的导数:
令 。
。
可知, ;
;
又 ;
所以, ,不等式得证。
命题二得证。
这两个不等式分别给出了 的下界初等函数和上界初等函数,作者将上下界函数取平均即得到 的一个逼近公式即逼近公式一。
逼近公式一:
x = 0时,右侧式子中有一个分母是4x,此时用极限求解,当x趋近于0得右侧式子为0.5,左侧N(0)也是0.5,此时是严格相等。
逼近公式一的误差图(横坐标为x的值,纵坐标为误差)如图3所示。
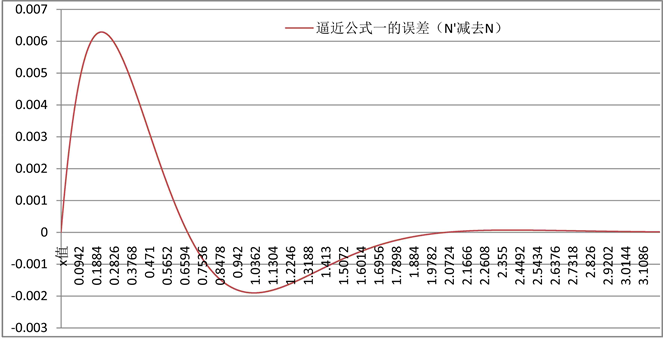
Figure 3. The error of the approximate formula one
图3. 逼近公式一的误差
逼近公式一未进行任何优化也取得了一定精度:最大的绝对误差是 ,x越大误差越小,当x大于2时,误差小于 。
该逼近公式是命题二的一个应用,命题二的价值在这里得到了一定程度体现。
为了引出命题三,考虑如下情形(设标的资产到期价格为 ):
卖出一份期权获得期权费C,同时买入 份标的资产,期权到期时再根据到期行情的价格支付期权买方所应得金额后,若此时的盈亏值在到期行情大于等于 的情况下(即 ),期望值为0,求解 (由命题二易知, )。
即 满足如下式子:
再结合 。
化简得方程:
从上式难以得出 的解析表达式,但作者发现三条性质:
命题三:
性质1: 为自变量,当 时, 近似地在一条直线上,直线拟合 = 0.9974。
性质2: 为自变量,当 时, 近似地在一条直线上,直线拟合 = 0.9992。
性质3: 为自变量,当 时, 非常近似地在一条直线上,直线拟合 = 0.9998,且
。
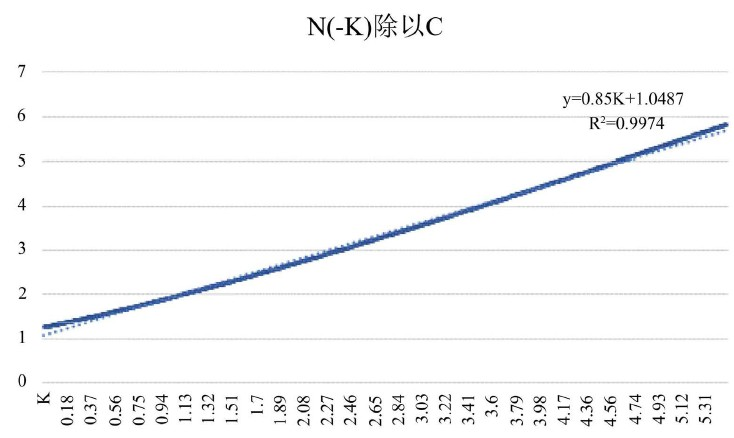
Figure 4. in a straight line approximately
图4. 近似在一条直线上
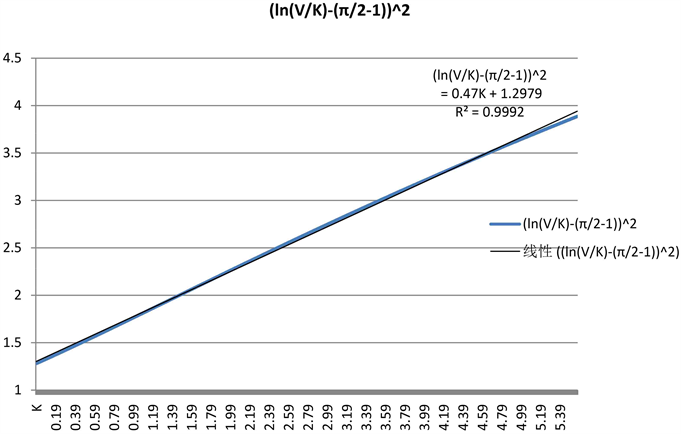
Figure 5. in a straight line approximately
图5. 近似在一条直线上
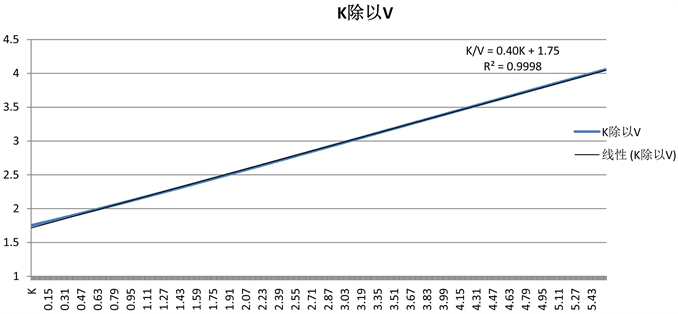
Figure 6. in a straight line approximately
图6. 近似在一条直线上
下面证明 :
方程左右两侧都对 求导并整理得:
当 趋向于0时,因 ,所以 也趋向于0。
将 代入上式得:
,即
命题三的应用:
由命题三的这三个近似直线的性质,作一定程度优化后可以再得到三个逼近公式。
为了论述方便,这里将自变量 换为 ,同时结合 ,再结合当 且较小时,有 。
由命题三的性质2得逼近公式二:
其中,
。
逼近公式三的误差图(横坐标为 的值,纵坐标为误差)如图7所示。
逼近公式二实现了高精度,最大的绝对误差是 。当x大于1.29时,随着x的增大,误差持续减小,当x = 3时,误差是 ,当x = 6时,误差是 。
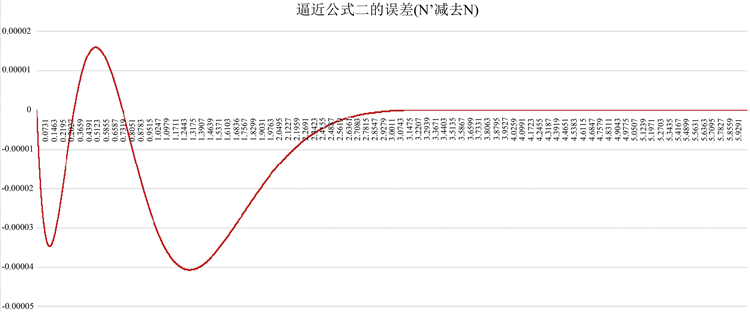
Figure 7. The error of the approximate formula two
图7. 逼近公式二的误差
将N和逼近公式二所得值 同时画在一张图表里,如下图,由于精度非常高所以图表中两曲线重叠了,如图8所示。

Figure 8. The comparison between the value obtained by the approximate formula two and the exact value
图8. 逼近公式二所得值和准确值的对比
由命题三的性质3得逼近公式三:
其中,
逼近公式三的误差图(横坐标为x的值,纵坐标为误差)如图9所示。
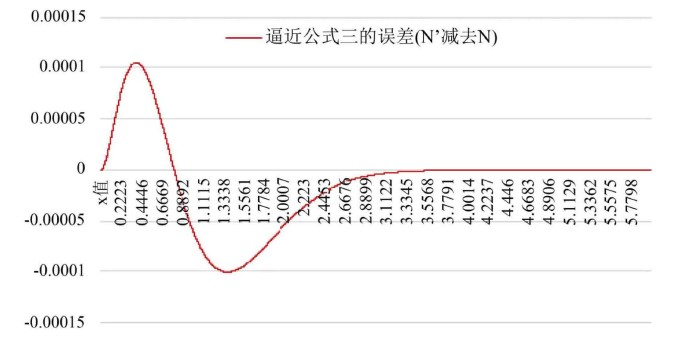
Figure 9. The error of the approximate formula three
图9. 逼近公式三的误差
逼近公式三也实现了较高精度,最大的绝对误差是 。精度高于逼近公式一,低于逼近公式二,但逼近公式三比逼近公式二简洁。
由命题三的性质1得逼近公式四:
逼近公式四的误差图(横坐标为x的值,纵坐标为误差)如图10所示。
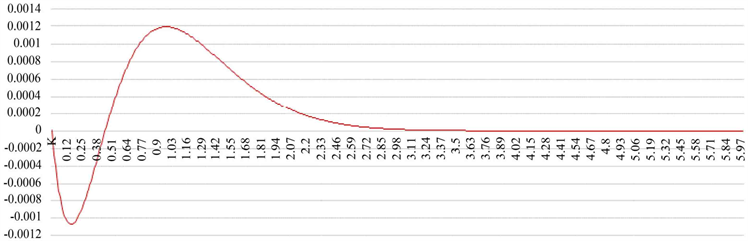
Figure 10. The error of the approximate formula four
图10. 逼近公式四的误差
逼近公式四最大的绝对误差是 。精度高于逼近公式一,低于逼近公式二,低于逼近公式三,但逼近公式四最简洁。
3. 结论
本文在随机游走行情期权复制的研究中提出三个命题。命题一从新的角度阐述期权复制原理并推导出一个数学等式。由命题二、命题三,发现了两个不等式、四个累积正态分布函数的近似初等函数。两个不等式给出了 的上下界,能帮助人们快速估算 的取值范围。四个累积正态分布函数的近似初等函数中,逼近公式二的近似精度最高,远高于逼近公式一的近似精度,但公式略微复杂。逼近公式四兼顾了精度和公式简洁性,应用时建议选择逼近公式四。
文章引用
汤大伟,蔡之卓. 随机游走行情期权复制的研究并推导出若干公式
Research on the Replication of the Option of Random Walk Market and Deducing Some Formulas[J]. 应用数学进展, 2019, 08(04): 826-837. https://doi.org/10.12677/AAM.2019.84093
参考文献
- 1. 盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 北京: 高等教育出版社, 2008.