Advances in Applied Mathematics
Vol.
10
No.
05
(
2021
), Article ID:
42683
,
8
pages
10.12677/AAM.2021.105179
利用Laplace变换求解时间分数阶Swift-Hohenberg方程
项诗景1,王倩倩1,谢歆2
1华侨大学数学科学学院,福建 泉州
2黄山学院数学与统计学院,安徽 黄山

收稿日期:2021年4月25日;录用日期:2021年5月8日;发布日期:2021年5月27日

摘要
针对时间分数阶Swift-Hohenberg方程,本文提出了基于Laplace变换的高效数值算法。首先利用Laplace变换将原Caputo型分数阶方程转化为整数阶方程,然后利用算子分裂法进一步将其分解成线性方程和非线性方程,其中,非线性方程通过积分法近似求解,线性方程通过Crank-Nicolson差分格式求解,最后通过数值实验验证了所给格式的有效性。
关键词
Swift-Hohenberg方程,Laplace变换,算子分裂法,Crank-Nicolson差分格式
Solving Time Fractional Swift-Hohenberg Equation Using Laplace Transform
Shijing Xiang1, Qianqian Wang1, Xin Xie2
1School of Mathematical Sciences, Huaqiao University, Quanzhou Fujian
2School of Mathematics and Statistics, Huangshan University, Huangshan Anhui

Received: Apr. 25th, 2021; accepted: May 8th, 2021; published: May 27th, 2021

ABSTRACT
For the time fractional Swift-Hohenberg equation, this paper proposes an efficient numerical algorithm based on Laplace transform. First, the Laplace transform is used to transfrom the original Caputo fractional equation into an integer-order equation, and then the operator splitting method is used to further decompose the equation into linear equation and nonlinear equation. The nonlinear equation is approximately solved by the integral method, and the linear equation is solved by the Crank-Nicolson scheme and central difference. Finally, the validity of the given scheme is verified through numerical experiments.
Keywords:Swift-Hohenberg Equation, Laplace Transform, Operator Splitting Method, Crank-Nicolson Difference Scheme

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
Swift-Hohenberg方程是1977年Swift和Hohenberg通过Rayleigh-Bénard不稳定球面波的模型 [1] 给出的,近年来相关研究涉及激光器 [2]、平面几何 [3]、时滞动力学 [4]、图灵分叉 [5] 等多方面,在物理学领域发挥着重要的作用,特别在流体力学和激光的对流问题中有着广泛应用。
关于Swift-Hohenberg方程的求解,中外研究者们已经提出了很多可行的解析方法和数值方法,例如指数法 [6]、同伦摄动法 [7] (Homotopy perturbation Method)、微分变换法 [7] (Differential Transform Method)、分数变分迭代法 [8] (Fractional Variational Iteration Method)、同伦分析法 [9] (Homotopy Analysis Method)等。
分数阶微积分诞生后的很长时间内,研究都局限在理论数学领域内,直到二十世纪七十年代,研究人员发现自然科学与工程领域的分形几何、记忆过程等相关现象与分数阶微积分存在密切的联系,才掀起了研究热潮。整数阶导数往往局限于某个物理过程在特定时刻的变化和性质,而分数阶导数模型既克服了经典整数阶微分理论模型实验结果吻合度低的缺点,又能较好地体现系统函数发展的历史依赖过程,为我们研究复杂物理力学问题提供了很大的帮助。
Riemann-Liouville型和Caputo型是目前最常用的两种分数阶导数的定义方式 [10]。观察发现,时间分数阶导数的计算常使用Caputo定义,而空间分数阶导数的计算更多使用Riemann-Liouville定义和级数定义,当然分数阶导数的不同定义也可以理解为不同的方法分别求解分数阶导数。
本文研究如下的时间分数阶Swift-Hohenberg方程:
(1)
其中, 是Caputo分数阶导数, 是函数 关于u的导,参数 , 都是具有物理意义的常量。
(2)
(3)
(4)
首先,利用Laplace变换逼近时间分数阶Swift-Hohenberg方程的分数阶项,将其转化为整数阶问题,然后,利用算子分裂法将得到的整数阶方程分解为线性部分和非线性部分,将解算子分别记为 和 ,最后通过以下格式求解,得到方程的数值解。其中,非线性部分利用左矩形法近似求解,线性部分利用Crank-Nicolson差分格式求解。
(5)
2. 分数阶Swift-Hohenberg方程的算子分裂法
2.1. Laplace变换
Laplace变换 [11] 是工程数学中常用的一种积分变化,在科学研究领域有广泛的应用。
(6)
运用分部积分法和Laplace变换公式可以得到以下微分性质:
(7)
将该微分性质推广到一般情况,可以得到:
(8)
Laplace逆变换就是实现以上过程的逆向变换。
(9)
研究发现 [12] [13],利用Laplace变换可以很好地将分数阶方程转化为整数阶方程,进而降低求解难度。现利用Laplace变换逼近Caputo型分数阶导数:
(10)
利用Lagrange插值实现 线性化,得到:
(11)
将式(11)代入式(10),得到:
(12)
对上式进行Laplace逆变换,整理后得到:
(13)
于是,时间分数阶Swift-Hohenberg方程可以转化为如下的整数阶方程:
(14)
2.2. 算子分裂法
算子分裂法 [14] 是一种偏微分方程数值解法,可以把复杂的算子分裂成几个可分别求解的简单子算子之积,实现复杂问题的简单化处理。
运用算子分裂法分解成两个子问题时,算子的顺序不影响计算结果,具体求解过程如下:
(1) 计算前半步长的算子 ,其中 ;
(2) 令 ,计算一个步长的算子 ,其中 ;
(3) 令 ,计算后半步长的算子 ,其中 。
取空间节点数为M,则空间步长 ;取时间节点数为N,则时间步长 。
空间方向的节点:
时间方向的节点:
利用算子分裂法将转化后的整数阶方程进行如下分解:
对于非线性方程式(15),方程两边同除以u,然后两边同时积分,可得:
(17)
对于线性方程式(16),利用Crank-Nicolson格式在时间方向的(k+1/2)层处逼近,可得:
(18)
(19)
注意, 和 利用线性插值给出,即:
(20)
两端边值条件均为零。
将已知的k 层和待求的k + 1层分别整理到等式的两边,得到矩阵:
(21)
其中 ,,,。
记左右两边矩阵分别为A和B,则待求的 层表示如下:
(22)
将式(17)和式(22)代入式(5),得到原方程的数值解:
(23)
3. 数值算例
3.1. 精度测试
验证该数值格式的精确性时,在原方程的基础上引入右端项 。
特殊的初值函数求分数阶导,有如下求解公式:
(26)
代入公式求解式(26)的分数阶项:
(27)
移项整理得到 的表达式:
(28)
选取区域范围 ,网格剖分 ,,,,,给出数值解图像和误差图像,分别如图1,图2所示。
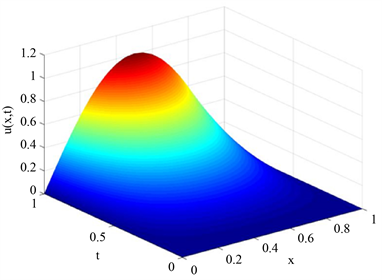
Figure 1. Numerical solution image
图1. 数值解图像
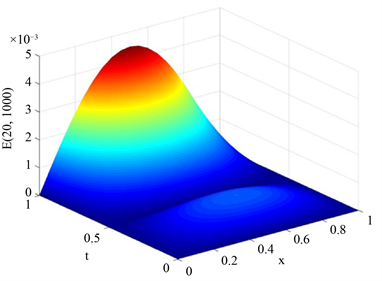
Figure 2. Error image
图2. 误差图像
选定时间方向的最后一层 ,给出最大相对误差 的计算公式:
(29)
其中, 和 分别对应节点 的精确解和数值解。
取定不同的时间和空间网格剖分,并改变参数值,列表观察最大相对误差变化,如表1所示。
Table 1. The maximum relative error of different time-space meshing and different parameter values
表1. 不同时空网格剖分和不同参数值的最大相对误差
观察发现,数值解逼近精确解具有较高的精度,并且空间方向网格剖分越密, 越小,精度越高。验证了本文所采用格式的有效性和精确性。
3.2. 长时间动力学行为
考虑如下初值问题:
(30)
两端的边值条件均为零,取定参数 ,,,时空剖分 ,给出 的数值解图像,时间方向最后一层 的数值解曲线,分别如图3,图4所示。
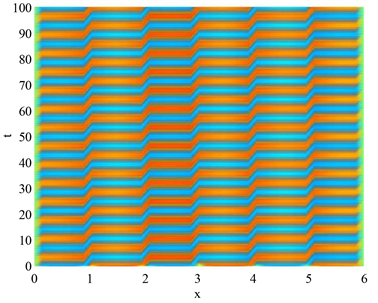
Figure 3. Numerical solution image ( )
图3. 数值解图像( )
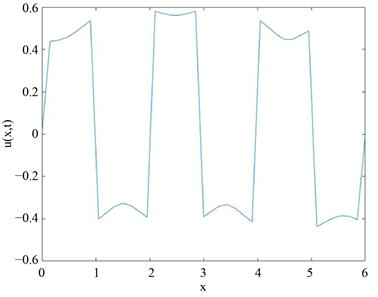
Figure 4. Numerical solution curve of
图4. 的数值解曲线
4. 结论
基于Laplace变换,将时间分数阶Swift-Hohenberg方程转化为整数阶Swift-Hohenberg方程,然后,利用算子分裂法将其进一步分解成两个子问题分别求解,最后通过数值算例验证格式的有效性。本文对Swift-Hohenberg方程的求解方法,为今后该方程的深入研究提供了有力的支持。
基金项目
2019年安徽省高校学科(专业)拔尖人才学术资助项目(gxbjZD38)。
文章引用
项诗景,王倩倩,谢 歆. 利用Laplace变换求解时间分数阶Swift-Hohenberg方程
Solving Time Fractional Swift-Hohenberg Equation Using Laplace Transform[J]. 应用数学进展, 2021, 10(05): 1681-1688. https://doi.org/10.12677/AAM.2021.105179
参考文献
- 1. Swift, J. and Hohenberg, P.C. (1977) Hydrodynamic Fluctuations at the Convective Instability. Physical Review A, 15, 319. https://doi.org/10.1103/PhysRevA.15.319
- 2. Lega, J., Moloney, J.V. and Newell, A.C. (1994) Swift-Hohenberg Equation for Lasers. Physical Review Letters, 73, 2978-2981. https://doi.org/10.1103/PhysRevLett.73.2978
- 3. Lloyd, D.J.B., Sandstede, B., Avitabile, D. and Champneys, A.R. (2008) Localized Hexagon Patterns of the Planar Swift-Hohenberg Equation. SIAM Journal on Applied Dynamical Systems, 7, 1049-1100. https://doi.org/10.1137/070707622
- 4. Zhang, C., Agarwal, R.P., Bohner, M. and Li, T. (2015) Oscillation of Fourth-Order Delay Dynamic Equations. Science China Mathematics, 58, 143-160. https://doi.org/10.1007/s11425-014-4917-9
- 5. Kuske, R., Lee, C.Y. and Rottschäfer, V. (2018) Patterns and Coherence Resonance in the Stochastic Swift-Hohenberg Equation with Pyragas Control: The Turing Bifurcation Case. Physica D: Nonlinear Phenomena, 365, 57-71. https://doi.org/10.1016/j.physd.2017.10.012
- 6. Zahra, W.K., Nasr, M.A. and Baleanu, D. (2020) Time-Fractional Nonlinear Swift-Hohenberg Equation: Analysis and Numerical Simulation. Alexandria Engineering Journal, 59, 4491-4510. https://doi.org/10.1016/j.aej.2020.08.002
- 7. Khan, N.A., Khan, N.-U., Ayaz, M. and Mahmood, A. (2011) Analytical Methods for Solving the Time-Fractional Swift-Hohenberg (S-H) Equation. Computers & Mathematics with Applications, 61, 2182-2185. https://doi.org/10.1016/j.camwa.2010.09.009
- 8. Khan, N.A., Riaz, F. and Khan, N.A. (2014) On Solutions of Nonlinear Time-Space Fractional Swift-Hohenberg Equation: A Comparative Study. Ain Shams Engineering Journal, 5, 285-291. https://doi.org/10.1016/j.asej.2013.09.001
- 9. Vishal, K., Kumar, S. and Das, S. (2012) Application of Homotopy Analysis Method for Fractional Swift Hohenberg Equation—Revisited. Applied Mathematical Modelling, 36, 3630-3637. https://doi.org/10.1016/j.apm.2011.10.001
- 10. 祝奔石. 分数阶微积分及其应用[J]. 黄冈师范学院学报, 2011, 31(6): 1-3.
- 11. 谭鑫贵. 分数阶导数模型理论的研究[D]: [硕士学位论文]. 湘潭: 湘潭大学, 2012: 12-13.
- 12. 时旭, 崔晨, 刘佳奇. 利用Laplace变换求解时间分数阶对流扩散方程[J]. 应用数学进展, 2020, 9(10): 1701-1709. https://doi.org/10.12677/AAM.2020.910197
- 13. 汪精英, 邓杨芳, 翟术英. 利用Laplace变换求解分数阶Allen-Cahn方程[J]. 华侨大学学报(自然科学版), 2020, 41(4): 549-554.
- 14. 王栋. 算子分裂法及其在解抛物型方程中的应用[D]: [硕士学位论文]. 长春: 吉林大学, 2009: 10-13.
