Pure Mathematics
Vol.
09
No.
03
(
2019
), Article ID:
30410
,
7
pages
10.12677/PM.2019.93061
The Reconstructing Problem for Hochstadt-Lieberman Theorem
Xianqing Zeng, Zhaoying Wei*, Jie Guo
College of Science, Xi’an Shiyou University, Xi’an Shaanxi

Received: Apr. 29th, 2019; accepted: May 9th, 2019; published: May 24th, 2019

ABSTRACT
In this paper we are concerned with the Hochstadt-Lieberman uniqueness theorem which states that, when the potential is known a priori on [0, 1/2], the full Dirichlet-Dirichlet spectrum of a Sturm-Liouville problem defined on the interval [0, 1] uniquely determines its potential. We shall give a new method for reconstructing the potential for this problem in terms of the Mittag-Leffler decomposition Theorem of meromorphic functions associated with the solution of Sturm-Liouville equantions. We also give a necessary and sufficient condition for the existence of the solution.
Keywords:Eigenvalue, Mittag-Leffler Expansion Theorem, Levin-Lyubarski Interpolation, Reconstruction Problem
Hochstadt-Lieberman定理的重构问题
曾献清,魏朝颖*,郭洁
西安石油大学理学院,陕西 西安

收稿日期:2019年4月29日;录用日期:2019年5月9日;发布日期:2019年5月24日

摘 要
Hochstadt-Lieberman唯一性定理表明,对于定义在[0, 1]区间上的Sturm-Liouville问题,若[0, 1/2]区间上的势函数已知,则一组Dirichlet-Dirichlet特征值即可唯一确定整个区间上的势函数。本文应用亚纯函数的Mittag-Leffler展开定理,给出了重构该问题势函数的一种新方法,同时给出了该问题的解存在的充要条件。
关键词 :特征值,Mittag-Leffler展开定理,Levin-Lyubarski插值,重构问题

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
1978年,Hochstadt与Lieberman [1] 证明了如下著名的Hochstadt-Lieberman唯一性定理:
定理1.1 对于定义在[0, 1]区间上的Sturm-Liouville算子 :
(1)
满足Dirichlet-Dirichlet (DD)边值条件:
, (2)
其中 为实值函数,若q在子区间 上已知,则一组Dirichlet-Dirichlet特征值 唯一确定 区间上的势函数q。
Martinyuk及Pivoarchik [2] 曾对以上唯一性定理给出了重构势函数的方法。本文的目的是对Hochstadt-Lieberman唯一性定理提供一种新的重构势函数的方法。通过应用Mittag-Leffler展开定理,将“较大的”全纯函数分解为两个“较小的”全纯函数,此分解为我们更好地使用Levin-Lyubarski插值公式重构全纯函数 及 提供了环境。此外,该重构方法亦给出了该问题的解存在且唯一的充要条件。
本文将用 表示定义在 上的型为a的指数类全纯函数 [3] 。
2. 势函数的重构
设 为方程(1)满足初始条件 及 的解。由文 [4] 可得:
, (3)
其中
, ,
满足以下积分方程:
,
且对于两个变量分别存在一阶偏导数。此外,
, . (4)
由(3)可得
(5)
其中 ,且对于 , 。
定义 为方程(1)满足初始条件 , 的解。则 具有类似于(3)的表达式:
. (6)
故 , 有如下渐近式:
(7)
其中 ,且对于 , 。
由于(1)~(2)的DD特征值 为特征值方程
(8)
的零点。由(3)可得,特征值函数的渐近式为:
, (9)
其中 。则当 时,DD特征值 的渐近式为:
(10)
其中 。
引理2.1 [5] [Theorem 3,6,2] 设
为亚纯函数,且当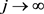 时,其单重极点
时,其单重极点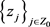 满足
满足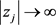 。记
。记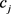 为
为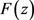 在
在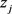 处的留数。若
处的留数。若
 , (11)
, (11)
则存在全纯函数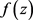 使得
使得
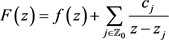 , (12)
, (12)
其中,(12)式右侧的级数在 上任何不包含点
上任何不包含点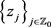 的有界子集上是一致收敛的。
的有界子集上是一致收敛的。
引理2.2 [6] [Theorem A]设f为sine类函数,其振幅宽度为2a,且其零点为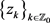 。则对于
。则对于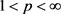 ,映射
,映射
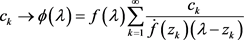 (13)
(13)
为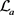 与
与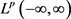 的同构映射,且在
的同构映射,且在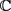 的任何子域上一致收敛。
的任何子域上一致收敛。
下面给出在 上重构q的方法及解存在的充要条件。定义
上重构q的方法及解存在的充要条件。定义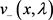 为方程(1)满足初始条件
为方程(1)满足初始条件 ,
,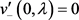 的解。类似可得
的解。类似可得
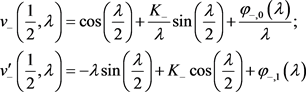 (14)
(14)
其中,对于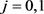 ,
,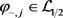 。记
。记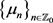 为
为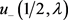 的零点,则
的零点,则
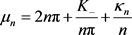 , (15)
, (15)
其中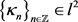 。显然
。显然 为亚纯函数且具有单重极点
为亚纯函数且具有单重极点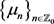 。设
。设 为函数
为函数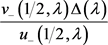 在
在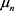 处的留数,则有
处的留数,则有
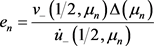 , (16)
, (16)
其中 。由(5),(8)及(10)可得
。由(5),(8)及(10)可得
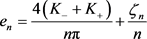 , (17)
, (17)
其中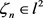 ,结合(15),可得
,结合(15),可得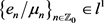 。由引理2.1,可知存在全纯函数
。由引理2.1,可知存在全纯函数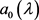 ,满足
,满足
 . (18)
. (18)
定义
 , (19)
, (19)
则可得
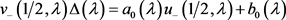 . (20)
. (20)
显然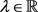 时,
时,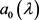 ,
,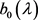 为全纯函数。
为全纯函数。
引理2.3 若记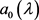 与
与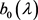 为
为
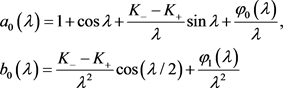 (21)
(21)
则 ,
,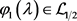 ,且
,且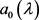 及
及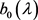 在展开式(20)中为唯一的。
在展开式(20)中为唯一的。
证明 注意到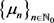 为
为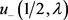 的零点,则由(20)可得
的零点,则由(20)可得
 (22)
(22)
将(15)带入计算,可得
 ,
,
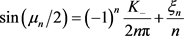 , (23)
, (23)
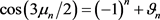 ,
,
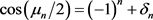 ,
,
其中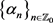 ,
,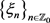 ,
, 均属于
均属于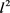 。进而将(23)带入(22)得到
。进而将(23)带入(22)得到
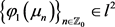 . (24)
. (24)
由于函数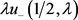 为sine类函数,且存在正整数
为sine类函数,且存在正整数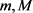 及p使得当
及p使得当 时,
时,
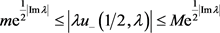
则结合(24),应用Levin-Lyubarski插值定理,即引理2.2,选取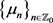 为重构函数
为重构函数 的插值节点,若记
的插值节点,若记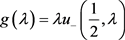 ,则有:
,则有:
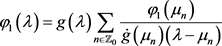 , (25)
, (25)
其中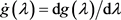 ,
,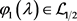 。
。
此外,Levin-Lyubarki插值定理保证了所重构函数的唯一性。故定理得证。
引理2.4 设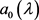 与
与 由(21)式定义。若
由(21)式定义。若
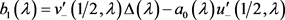 , (26)
, (26)
则
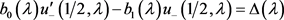 . (27)
. (27)
进而有
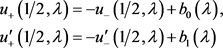 (28)
(28)
证明 由于
 , (29)
, (29)
计算易得(27)成立。由于
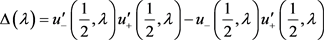 (30)
(30)
且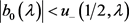 ,式(30)结合(27),可知存在
,式(30)结合(27),可知存在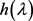 满足
满足
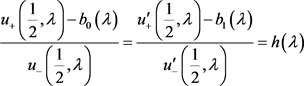 . (31)
. (31)
由(5)及(7)可知,当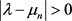 时,有
时,有
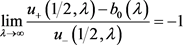 ,
,
故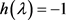 ,从而可得(28)。定理得证。
,从而可得(28)。定理得证。
注1 由引理2.3可知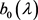 是唯一的. 由引理2.4可得
是唯一的. 由引理2.4可得 的表达式,进而可得
的表达式,进而可得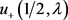 与
与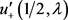 ,故有如下结论:
,故有如下结论:
定理2.5 设函数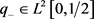 ,数列
,数列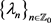 已知,且满足如下渐近式:
已知,且满足如下渐近式:
 (32)
(32)
其中A, ,
,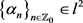 。若
。若
 (33)
(33)
其中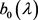 ,
,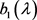 分别由(21)与(26)定义,且
分别由(21)与(26)定义,且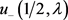 ,
,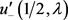 由(5)定义。
由(5)定义。
则存在唯一的实值函数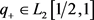 ,使得势函数q在
,使得势函数q在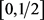 上满足
上满足 ,在
,在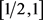 上,
上,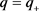 ,且其对应的算子以
,且其对应的算子以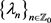 为特征值的充要条件是
为特征值的充要条件是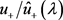 属于Nevanlinna类函数。
属于Nevanlinna类函数。
证明 必要性:假定存在实值函数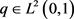 ,使得
,使得 为Sturm-Liouville算子的DD特征值。则由以上讨论可知,
为Sturm-Liouville算子的DD特征值。则由以上讨论可知,
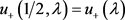 ,
, .
.
故由 [2] [7] 知,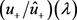 是Sturm-Liouville问题(1)~(2)的Weylm-函数 [7] ,故
是Sturm-Liouville问题(1)~(2)的Weylm-函数 [7] ,故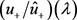 属于Nevanlinna类函数。
属于Nevanlinna类函数。
充分性:若实值函数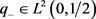 已知,则函数
已知,则函数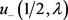 、
、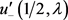 及
及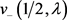 ,
,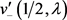 为已知函数。则由(5)、(14)及引理2.3得,
为已知函数。则由(5)、(14)及引理2.3得,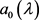 及
及 可知,又由于DD特征值已知,进而由(26)可得
可知,又由于DD特征值已知,进而由(26)可得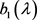 ,从而由(28)计算可得
,从而由(28)计算可得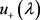 及
及 :
:
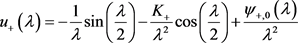 ,
,
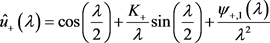 ,
,
其中 ,故
,故 可知。定理得证。
可知。定理得证。
基金项目
国家自然科学基金面上项目资助(11571212);陕西省大学生创新训练项目资助(1314)。
文章引用
曾献清,魏朝颖,郭 洁. Hochstadt-Lieberman定理的重构问题
The Reconstructing Problem for Hochstadt-Lieberman Theorem[J]. 理论数学, 2019, 09(03): 458-464. https://doi.org/10.12677/PM.2019.93061
参考文献
- 1. Hochstadt, H. and Lieberman, B. (1978) An Inverse Sturm-Liouville Problem with Mixed Given Data. SIAM Journal on Applied Mathematics, 34, 676-680.
https://doi.org/10.1137/0134054 - 2. Martinyuk, O. and Pivovarchik, V. (2010) On the Hochstadt-Lieberman Theorem. Inverse Problems, 26, Article ID: 035011, 6 p.
https://doi.org/10.1088/0266-5611/26/3/035011 - 3. Levin, B.J. (1980) Distribution of Zeros of Entire Functions. American Mathematical Society, Providence, RI.
- 4. Marchenko, V. (1986) Sturum-Liouville Operators and Applications. Birkhäuser, Ba-sel.
- 5. Ablowitz, M.J. and Fokas, A.S. (2003) Complex Variables Introduction and Applications. 2nd Edition, Cambridge Univer-sity Press, Cambridge.
- 6. Levin, B. and Yu, I. (1975) Lyubarskii, Interpolation by Entire Functions of Special Classes and Related Expansions in Series of Exponents. Izvestiya Rossiiskoi Akademii Nauk USSR, 39, 657-702. (In Russian)
https://doi.org/10.1070/im1975v009n03abeh001493 - 7. Gesztesy, F. and Simon, B. (2000) Inverse Spectral Analysis with Partial Information on the Potential II: The Case of Discrete Spectrum. Transactions of the American Mathematical Society, 352, 2765-2787.
NOTES
*通讯作者。