Pure Mathematics
Vol.
13
No.
03
(
2023
), Article ID:
63422
,
10
pages
10.12677/PM.2023.133071
对带熵的随机线性二次最优控制问题的收敛性证明
舒心
上海理工大学理学院,上海
收稿日期:2023年2月22日;录用日期:2023年3月23日;发布日期:2023年3月30日

摘要
本文通过矩阵变换将带熵的随机线性二次最优控制问题的解转化为其等价形式后,证明了线性二次方程的二次项系数解的唯一性和迭代式的收敛性,而一次项系数为0,常数项系数只与二次项有关,控制过程的最优概率分布也只与二次项有关。然后用蒙特卡洛随机抽样样本的均值估计期望值,由此设置了算法1,并证明了算法1中的迭代式具有波动性,波动率的大小和随机参数的方差有关,也与蒙特卡洛中的样本数有关,样本数越多,波动对应的方差越小。然后用两个数值案例比较了随机逼近Q-learning算法和蒙特卡洛Q-learning算法,相同迭代次数下,随机逼近Q-learning算法计算时间更少,但误差更大,蒙特卡洛Q-learning算法收敛更快更稳定,并且可以通过增加随机抽取的样本数使误差更小。
关键词
随机线性二次最优控制,收敛性,Q-Learning,蒙特卡洛,随机逼近

The Proof of the Convergence of Stochastic Linear Quadratic Optimal Control Problem with Entropy
Xin Shu
College of Science, University of Shanghai for Science and Technology, Shanghai
Received: Feb. 22nd, 2023; accepted: Mar. 23rd, 2023; published: Mar. 30th, 2023

ABSTRACT
In this paper, after transforming the solution of the stochastic linear quadratic optimal control problem with entropy into its equivalent form through matrix transformation, we prove the uniqueness of the solution of the quadratic coefficient of the linear quadratic equation and the convergence of the iterative formula, and the result shows that the coefficient of the first term is 0, the coefficient of the constant term is only related to the quadratic term, and the optimal probability distribution of the control process is only related to the quadratic term. Then, the mean value of random sampling samples in Monte Carlo is used to estimate the expected value, thus algorithm 1 is set up, and it is proved that the iterative formula in algorithm 1 has volatility, the volatility is related to the variance of random parameters and the number of samples in Monte Carlo, the more sample number, the smaller the variance of the fluctuation. Then, two numerical cases are used to compare Q-learning algorithm with stochastic approximation and Q-learning algorithm with Monte Carlo. Under the same number of iterations, Q-learning algorithm with stochastic approximation takes less time to compute, but the error is larger. Q-learning algorithm with Monte Carlo converges faster and more stable. Moreover, the error can be reduced by increasing the number of randomly selected samples.
Keywords:Stochastic Linear Quadratic Optimal Control, The Convergence, Q-Learning, Monte Carlo, Stochastic Approximation

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
因为广泛的应用背景,线性二次最优控制问题已经有了很多研究 [1] - [6] ,根据 [7] 可知,对于给定初始状态 ,系统
对应的折扣问题的价值函数为
的随机线性二次控制问题,可以根据控制过程的概率分布,用熵增加对控制过程的探索。其中 是 下的可行性控制分布集, 是t时刻时状态x控制概率为 下的即时奖励。假设值函数为二次型时 ,可求得随机控制的最优概率分布
并根据概率分布可以求得线性二次最优控制各项系数的迭代式:
其中的函数映射定义为
根据推导出来的系数的迭代公式定义函数
由此可得到
所以最终 , 。
参考文献 [7] 只给出了问题解的迭代形式,但是没有证明解的唯一性以及根据迭代式算得的结果的收敛性。因此本文在参考文献 [7] 的基础上继续研究,证明了 和 解的唯一性,同时确定 ,所以在后续计算过程中不需要再继续计算 ,减少了计算过程。然后证明了当期望可准确求出时,迭代得到的 是收敛的,但使用蒙特卡洛近似期望后, 具有波动性,波动方差与随机参数有关,但是也可以通过调节蒙特卡洛方法中的随机抽样样本数来减少误差。
2. 解的唯一性
为了求得 和 ,使用迭代式
但是参考文献 [7] 没有证明 解的唯一性以及 的收敛性,因此本文继续证明Q值的收敛问题。假设线性二次最优控制问题有解,可以将问题转化为等价形式再求解。假设 是有限的, 是正定矩阵。首先定义一个关于 的函数
所以
根据文献 [6] 的Theorem1.1可知 有唯一解, 是收敛的。
然后证明 的收敛性。因为 是正定的,所以存在 使得 (矩阵 意味着 是半正定矩阵),所以
同理 ,令L和M为可逆矩阵且
根据文献 [6] 的证明过程,定义一个 的矩阵
其中 是矩阵 的子矩阵运算的简化形式。利用矩阵C首先对 及相关矩阵做矩阵变换
变换后的矩阵具有以下关系
然后对矩阵 做变换
变换后可得到以下关系式
然后定义一个关于 的函数
根据T函数定义可得 ,因为 可以推得 ,又因为 的性质 ,所以存在一个正数 使得
根据矩阵2范数的定义知 , 表示为 的最大特征值,因为 ,所以 ,所以
所以 是关于矩阵2范数的压缩映射,且不动点为0。所以对于迭代式
此时 是收敛的。
又因为 ,所以 是 的不动点,由不动点唯一性可得 ,所以最终线性二次问题只需要求二次项系数 和常数项 的值。
3. 算法及其收敛性
根据Q-learning算法,迭代公式为
因为参数是随机的,所以无法求得准确期望值,因此使用蒙特卡洛法求期望的近似值。蒙特卡洛由Metropolis [8] 提出,是根据随机抽样来估计数学函数或者复杂系统 [9] 。蒙特卡洛应用广泛于不同领域,目前已有大量理论研究和实践经验 [10] [11] [12] 。蒙特卡洛通过随机抽样生成大量样本,然后用样本统计量估计问题的解。本文中使用抽样样本均值来估计期望值,计算方法为
其中s为随机生成的样本数,本文中设置样本数量为s = 200。由此设置算法1,见表1。其中学习率满足 , 。
Table 1. Q-learning algorithm with Monte-Carlo
表1. 蒙特卡洛Q-learning算法
然后证明算法1 (见表1)中 的收敛性。根据算法1中的迭代式定义关于 的一个函数
所以 ,可以转化为以下等式
因为前半部分 是收敛的,所以主要考虑 的收敛性。因为随机变量独立同分布,所以 ,所以 ,令 ,
这里的方差代表着矩阵的协方差矩阵,因为方差不为0,所以算法1中的 不收敛。根据方差计算结果可知, 在一定范围内波动,波动率与随机参数的方差有关,也与随机生成抽样的样本数有关,样本数越多,对应的方差越小。
然后根据随机逼近理论考虑另一种算法。Robbins-Monro首创了随机逼近理论 [13] ,然后被快速应用到随机优化问题中 [14] [15] 。随机逼近算法是为了解决寻根问题,其中的函数是一个期望值。 [16] 结合随机逼近思想证明了Q-learning的收敛性, [6] 将随机逼近算法应用到线性二次问题中。根据文献 [6] ,本文也考虑使用随机逼近算法。根据随机逼近思想,迭代式为
因此设置算法2,见表2。Dai [6] 已经证明线性二次问题中使用随机逼近的Q-learning算法是收敛的。
Table 2. Q-learning algorithm with stochastic approximation
表2. 随机逼近Q-learning算法
4. 数值分析
比较两种算法的可行性和有效性,选择两个不同的例子,其中折扣因子 ,算法中的学习率 。首先考虑状态空间 ,控制空间 时的情况,此时使 , ,其中 , 独立同分布且服从标准正态分布。
,
,
根据算法收敛性证明过程知道,蒙特卡洛算法的波动大小和随机抽样的样本数有关,样本量越大方差越小。
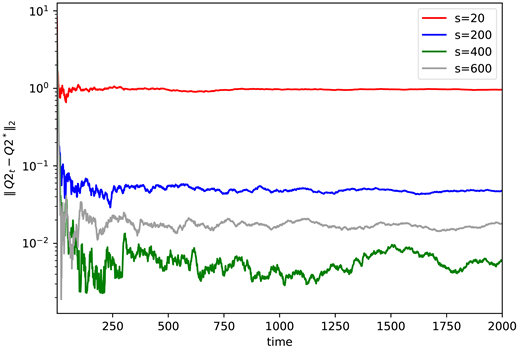
Figure 1. The convergence for different values of s
图1. s取不同值时的收敛情况
由图1可以看出,随着抽样数s的增加,误差越来越小(见图1)。蒙特卡洛Q-learning可以通过改变s值来控制误差,但是抽样数s越大计算所需时间也越长,因此从计算时长和精确度考虑,选s = 200。
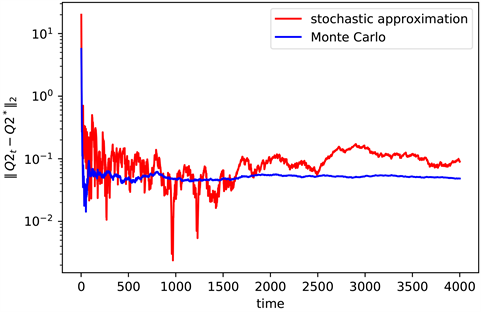
Figure 2. The convergence of Q2 when n = 2
图2. n = 2时Q2的收敛情况

Figure 3. The convergence of K0 when n = 2
图3. n = 2时K0的收敛情况
图2是状态空间 时,不同算法下真实值 与算法计算出来的值 之间的差值取对数后的结果(见图2),图3是根据 计算得到 (见图3)。
然后考虑状态空间 ,控制空间 时的情况,令 ,其中 标准正态分布。
,
,
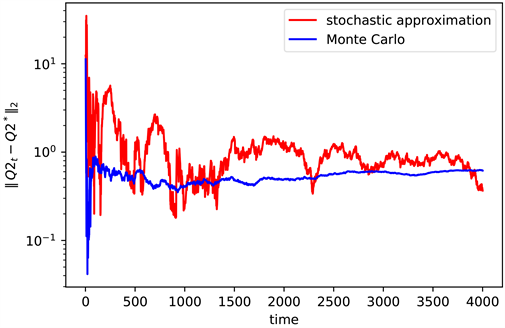
Figure 4. The convergence of Q2 when n = 3
图4. n = 3时Q2的收敛情况
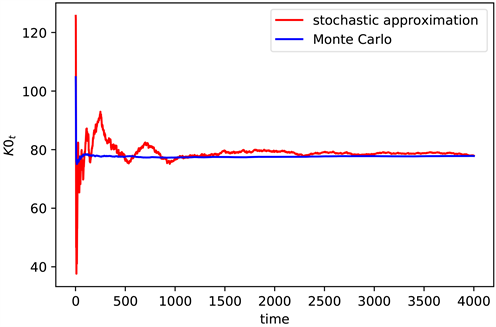
Figure 5. The convergence of K0 when n = 3
图5. n = 3时K0的收敛情况
同样的,图4是状态空间 时,不同算法的计算误差取对数后的值(见图4),图5是对应的 结果(见图5)。
根据数值实例的运算结果可以看出,通过改变抽取的随机样本的个数,我们可以很容易地改变蒙特卡洛Q-learning算法的精确度。对于不同的实例两种算法都能使结果趋近于真实值。蒙特卡洛Q-learning算法收敛更快更稳定误差值更小,迭代次数大于1000次以后,误差值就趋于稳定,而随机逼近Q-learning算法计算的结果误差一直存在波动,误差总体大于蒙特卡洛Q-learning算法。在相同迭代次数下,随机逼近Q-learning算法计算时间所用更少,蒙特卡洛Q-learning算法计算结果更准确。
5. 结论
本文在原有加熵的随机线性二次最有控制问题的基础上,证明了解的唯一性,然后证明了算法中迭代式的收敛性。结果表示对于一般形式的线性二次最优控制问题,加熵后根据贝尔曼原理求得的一次项系数为零,常数项系数只与二次项系数有关,由此在后续计算中只需要计算二次项系数与常数项系数的值,减少了运算步骤。然后证明了蒙特卡洛Q-learning算法中,由于用样本均值代替原有期望,所以根据迭代式求得的值具有波动性,波动率大小和随机参数的方差有关,也与蒙特卡洛算法中选取的样本数量有关,样本数量越多对应的方差越小,反之波动越大。最后比较了蒙特卡洛Q-learning算法和随机逼近Q-learning算法。迭代相同次数下随机逼近Q-learning算法计算更快,蒙特卡洛Q-learning算法收敛更快更稳定,而且可以通过改变s值的大小改变算法的准确度。
致谢
感谢导师的辛苦指导,给了我很多意见和帮助。感谢师兄师妹的鼓励和帮助。
文章引用
舒 心. 对带熵的随机线性二次最优控制问题的收敛性证明
The Proof of the Convergence of Stochastic Linear Quadratic Optimal Control Problem with Entropy[J]. 理论数学, 2023, 13(03): 659-668. https://doi.org/10.12677/PM.2023.133071
参考文献
- 1. Pronzato, L., Kulcsár, C. and Walter, E. (1996) An Actively Adaptive Control Policy for Linear Models. IEEE Trans-actions on Automatic Control, 41, 855-858. https://doi.org/10.1109/9.506238
- 2. Chen, S., Li, X. and Zhou, X.Y. (1998) Stochastic Linear Quadratic Regulators with Indefinite Control Weight Costs. SIAM Journal on Control and Optimization, 36, 1685-1702. https://doi.org/10.1137/S0363012996310478
- 3. Chen, S. and Zhou, X.Y. (2000) Stochastic Linear Quadratic Regulators with Indefinite Control Weight Costs. II. SIAM Journal on Control and Opti-mization, 39, 1065-1081. https://doi.org/10.1137/S0363012998346578
- 4. Rami, M.A., Moore, J.B. and Zhou, X.Y. (2002) Indefinite Stochastic Linear Quadratic Control and Generalized Differential Riccati Equation. SIAM Journal on Control and Optimization, 40, 1296-1311. https://doi.org/10.1137/S0363012900371083
- 5. Wang, T., Zhang, H. and Luo, Y. (2016) Infinite-Time Sto-chastic Linear Quadratic Optimal Control for Unknown Discrete-Time Systems Using Adaptive Dynamic Programming Approach. Neurocomputing, 171, 379-386. https://doi.org/10.1016/j.neucom.2015.06.053
- 6. Du, K., Meng, Q. and Zhang, F. (2022) A Q-Learning Algo-rithm for Discrete-Time Linear-Quadratic Control with Random Parameters of Unknown Distribution: Convergence and Stabilization. SIAM Journal on Control and Optimization, 60, 1991-2015. https://doi.org/10.1137/20M1379605
- 7. 舒心. 带熵的随机线性二次最优控制问题[J]. 应用数学进展, 2022, 11(12): 8836-8845. https://doi.org/10.12677/AAM.2022.1112931
- 8. Metropolis, N. and Ulam, S. (1949) The Monte Carlo Method. Journal of the American Statistical Association, 44, 335-341. https://doi.org/10.1080/01621459.1949.10483310
- 9. Harrison, R.L. (2010) Introduction to Monte Carlo Simu-lation. AIP Conference Proceedings, 1204, 17-21. https://doi.org/10.1063/1.3295638
- 10. James, F. (1980) Monte Carlo Theory and Practice. Reports on Progress in Physics, 43, Article No. 1145. https://doi.org/10.1088/0034-4885/43/9/002
- 11. Glasserman, P. (2004) Monte Carlo Methods in Financial En-gineering. Springer, New York. https://doi.org/10.1007/978-0-387-21617-1
- 12. Ferrenberg, A.M. and Swendsen, R.H. (1988) New Monte Carlo Technique for Studying Phase Transitions. Physical Review Letters, 61, 2635-2638. https://doi.org/10.1103/PhysRevLett.61.2635
- 13. Robbins, H. and Monro, S. (1951) A Stochastic Approximation Method. The Annals of Mathematical Statistics, 22, 400-407. https://doi.org/10.1214/aoms/1177729586
- 14. Lai, T.L. (2003) Stochastic Approximation. The Annals of Statistics, 31, 391-406. https://doi.org/10.1214/aos/1051027873
- 15. Nemirovski, A., Juditsky, A., Lan, G. and Shapiro, A. (2009) Robust Stochastic Approximation Approach to Stochastic Programming. SIAM Journal on Optimization, 19, 1574-1609. https://doi.org/10.1137/070704277
- 16. Tsitsiklis, J.N. (1994) Asynchronous Stochastic Approximation and Q-Learning. Machine Learning, 16, 185-202. https://doi.org/10.1007/BF00993306
