Computer Science and Application
Vol.
09
No.
02
(
2019
), Article ID:
29075
,
6
pages
10.12677/CSA.2019.92052
The Assessment of Gross Error in Equal Precision Measurement and the Fulfillment on Mathematica
Haizhen Miao
Fujian Jiangxia University College of Information Science and Electronics, Fuzhou Fujian
Received: Feb. 10th, 2019; accepted: Feb. 21st, 2019; published: Feb. 28th, 2019

ABSTRACT
Since the errors caused by accidental factors are called gross errors, it is very important to determine and eliminate gross errors in data series in equal precision measurement for the best value, uncertainty and confidence probability of measurement results, which will directly affect the best expression of measurement results and the reliability of relative errors. This paper discussed the determination and treatment process of gross error from the probability point of view, and explained how to implement the process on the tools of Mathematica. The conclusion can also be applied to the engineering practice.
Keywords:Equal Precision Measurement, Normal Distribution Function, Standard Deviation, Mathematica
等精度测量中粗大误差的评估及其在Mathematica上的实现
苗海珍
福建江夏学院电子信息科学学院,福建 福州
收稿日期:2019年2月10日;录用日期:2019年2月21日;发布日期:2019年2月28日

摘 要
由于偶然因素带来的误差称之为粗大误差,在等精度测量中,判定和剔除数据系列中的粗大误差,对测量结果的最佳值、不确定度、置信概率都十分重要,将直接影响到测量结果的最佳表达式和相对误差的可信程度。本文从置信概率的角度,探讨粗大误差的判别和处理过程,以及如何在数学工具Mathematica上实现的。这种结论同样可以应用到工程实践中。
关键词 :等精度测量,正态分布函数,标准偏差,Mathematica

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
大学物理实验中,关于测量及测量数据的分析处理是基本的和必选的实验之一。目的是使学生掌握科学实验的基础知识、基本实验方法和基本技能,培养科学严谨的治学精神和素养。传统的相关实验中,只是重点分析了随机误差和系统误差的产生原理和解决的方法,从这两方面提高测量的精确度、准确度和精密度。由于一个测量值的误差是由系统误差、随机误差和粗大误差共同组成的,对于粗大误差,则是由于实验者的粗心、外部环境和测量条件突变或干扰引起的。
一般情况下,粗大误差是显而易见的,可以在大量的测试数据中很容易地被发现。但这仅仅是当粗大误差达到一定的程度,由量变到了质变而被发现的。对粗大误差的判别带有相当程度的主观意志。如何从数学的角度,使用数学工具对粗大误差进行定义、界定和剔除,则鲜见与教科书和相关杂志文章。因此在相当部分的实验教科书里,对粗大误差的处理,也仅仅是要求剔除该次测量而已。
本文试图解决这一问题,对粗大误差不再进行主观判断,通过数学建模,由数学模型对粗大误差进行判断和处理,更进一步地避免人为干扰。
2. 等精度测量中的测量结果表达式
在科学实验中,为了数据的准确可信更接近于真实值,往往要对某个物理量进行多次重复测量,在测量过程中,还要保持测量环境、测量条件、测量方法、测量仪器和测量人员的一致性。当测量次数 充分大时( ),实验和理论都表明,测量数据项呈正态分布函数 [1] :
其中: ——总体平均值
——正态分布标准偏差
其物理意义为:当测量次数 充分大时( ),测量的总体平均值 可认为是测量值的真值,即: 。测量项落在 和 区间内的概率为68.3%。这时,就可以认为测量结果是的准确的,并且其可信程度为68.3%。
实际应用中,测量次数 都是有限次的,根据我国国家标准GB776-76的规定,科学研究中 ,大学实验中 。
一般意义上,被测量值的真值永远无法知晓,测量只能做到尽可能地接近真值,并且表明这个测量值的可信程度。即,一个测量值的最终结果只能表达为:
(单位)
其中: :待测物理量
:直接测量的算术平均值
:本次测量的总的不确定度,表明了本次测量的可信程度。大学实验中: 。
B类不确定度来自实验中的仪器,不属于本文讨论的范围,A类不确定度来自测量的随机误差,表征就是置信概率,在有限次测量中,该置信概率的计算使用平均值标准偏差,即:
在实践中,一个测量值的表达式由下列三项组成(未考虑B类不确定度):
测量结果表达式: (单位)---(1)
相对误差: ---(2)
置信概率: ----(3)
3. 粗大误差对测量的影响
测量过程中,不可避免地受到各种因素的影响:环境、温度、偶然因素干扰、操作人员的心理状态……等。对一组等精度测量数据进行比对,可以找到在这一系列数据项中,或多或少地存在若干数据项,这些数据项的值明显与其他大多数数据项有较大的差距,表明在该次测量中,由于某些偶然的因素,导致测量数据出现明显的差距,这种误差称之为粗大误差。
粗大误差对待测物理量的最佳估计值(算术平均值)和可信度都有影响,如图1所示的某次等精度测量的测量数据。 为原始的测量数据,未剔除粗大误差时的正态分布, 经过修正,剔除粗大误差后,组成新的数据列,得到的正态分布。粗大误差的结果导致标准偏差比较大。而经过粗大误差的剔除,标准偏差比较小。表明在相同的置信概率下,如果不考虑粗大误差对算术平均值 的影响,没有剔除粗大误差时,待测物理量的最佳估计值在一个相对宽泛的数据区间内可信;而剔除粗大误差后,待测物理量的最佳估计值则在一个相对狭小的数据区间内可信。它的物理意义是,经过粗大误差的剔除,测量的精密度得到提高。而衡量一个测量是否成功,需要从精密度、准确度和精确度三方面考量。测量的精密度表明了等精度测量所得数据的相互接近程度(离散程度)。测量结果的精密度高,说明所得结果的重复性好,测量数据的离散小,测量误差分布密集,随机误差小。
4. 粗大误差的剔除
粗大误差的剔除方法有肖维涅准则、罗曼诺夫斯基准则和格拉布斯准则等,其中肖维涅准则经常使用在大学实验和工程试验中。
粗大误差剔除的肖维涅准则,若一组测量值,其中某次测量值的偏差的绝对值与该组的标准偏差之比大于某一阈值,则该测量值为粗大误差,应予剔除。即:
当 时
被认为是粗大误差。

Figure 1. Measured data of equal precision measurement
图1. 某次等精度测量的测量数据
其中: 为肖维涅准则系数,对于大学实验, ,对于工程实践 (莱以达准则)。
需要注意的是,每次只能剔除一个粗大误差,剔除后重新计算 和 ,再运用肖维涅准则,直至所有 满足 ,就可以认为,待测物理量的数据列中,不再包含粗大误差。
5. Mathematica简介
Mathematica是由美国科学家斯蒂芬·沃尔夫勒姆领导的沃尔夫勒姆研究公司开发的一款使用的计算软件。它拥有强大的数值计算和符号运算能力。它是目前为止使用最广泛的数学软件之一。广泛地应用于物理学、工程学、数学、生物和社会学等众多领域 [2] 。
利用Mathematica内置函数,可以对一组数据列进行各种统计运算,如统计平均值、平均绝对偏差、方均根、样本方差和标准方差等。通过编程方式,实现粗大误差的自动剔除。
6. 处理过程及数据可视化
处理过程如图2所示

Figure 2. Processing procedure
图2. 处理过程
主要函数介绍如下:
Mean [list]:给出列表list中元素的统计平均值;
Standard Deviation [list]:给出list中元素的标准差;
Variance [list]:给出list中元素的样本方差;
Normal Distribution [ , ]:表示一个正态分布(高斯分布),它的均值为 ,标准差为 [3] ;
PDF [dist, x]:给出关于在 处的符号分布dist的概率密度函数 [4] ;
:绘制函数 的图线,其自变量 位于从 到 的区间上 [5] 。
如表1所示的是对某一物理量的等精度测量结果,各项数据的单位均是CM。
Table 1. Result of equal precision measurement
表1. 某一物理量的等精度测量结果
主要代码如下:
(*剔除粗大误差*)
While[True,
If [data=Abs[Min[datalist]-databest]>2*datasd,{datalist=Delete[datalist,1],
datalenth=Length[datalist],
databest=Mean[datalist],
datasd=StandardDeviation[datalist]},y=1];
If[y==1,Break[]]
While[True,
If [data=Abs[Max[datalist]-databest]>2*datasd,{datalist=Delete[datalist,-1],
datalenth=Length[datalist],
databest=Mean[datalist],
datasd=StandardDeviation[datalist]},x=1];
程序执行结果如下:
(*未剔除粗大误差*)
数据列:{9.05,9.07,9.55,9.72,9.78,9.82,9.83,9.96,9.98,10,10.05,10.06,10.07,10.09,10.1,10.1}
数据列长度:16
数据列平均值:9.82688
数据列标准偏差:0.33858
(*剔除粗大误差*)
数据列:{9.72,9.78,9.82,9.83,9.96,9.98,10,10.05,10.06,10.07,10.09,10.1,10.1}
数据列长度:13
数据列平均值:9.97
数据列标准偏差:0.133637
平均值标准偏差:0.0370644
A类不确定度:0.04
测量结果表达式: (CM)
相对误差:
置信概率:
图3表示了没有考虑粗大误差时的精密度和剔除粗大误差后的精密度。显而易见,剔除粗大误差后的数据列精密度远远好于前者。
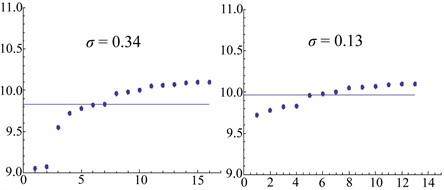
Figure 3. Precision without considering gross errors precision after eliminating gross error
图3. 没有考虑粗大误差时的精密度和剔除粗大误差后的精密度
7. 在工程实践中的应用
工程实践中,往往要对某项数据在实验室里反复试验,重复次数上百次甚至上千次,从而得到一个相对准确的数据,然后再应用到实际的工程中。例如,某种混凝土中需要的添加剂,每单位需要多少,除了理论计算外,还需要反复试验,由试验中得到一个可信的数据。
这里剔除的不再是粗大误差,而是那些不那么可靠离散比较大的试验数据。
8. 结论
在大学物理实验中,对于有限次的等精度测量,受环境偶然因素、尤其是初年级大学生,初次接触大学物理实验,没有相应的训练和技能,或多或少都会为测量数据带来粗大误差。如何判断和剔除粗大误差,进而对学生的实验成绩进行考核和评价,则可通过本文所介绍的方法,除对学生的技能和动手能力考核外,还可通过如图三所示的曲线,对实验的精密度进行考核。
文章引用
苗海珍. 等精度测量中粗大误差的评估及其在Mathematica上的实现
The Assessment of Gross Error in Equal Precision Measurement and the Fulfillment on Mathematica[J]. 计算机科学与应用, 2019, 09(02): 458-463. https://doi.org/10.12677/CSA.2019.92052
参考文献
- 1. 李汉龙, 主编. Mathematica基础及其在数学建模中的应用[M]. 北京: 国防工业出版社, 2016.
- 2. Grozin, A. (2015) Introduc-tion to Mathematica® for Physicists. Springer, Softcover Reprint of the Original.
- 3. Wolfram, S. (2016) An Elementary Introduction to the Wolfram Language. Wolfram Media Inc.
- 4. Napolitano, J. (2018) A Mathematica Primer for Physicists. CRC Press, Boca Raton.
- 5. (美)克里夫•黑斯廷斯, 等. Mathematica实用编程指南[M]. 北京: 科学出版社, 2018.
