Advances in Applied Mathematics
Vol.
10
No.
04
(
2021
), Article ID:
41889
,
6
pages
10.12677/AAM.2021.104119
一类带有导数项的非线性薛定谔方程的行波解
成蓉华1,项琳2*
1云南财经大学,云南 昆明
2浙江工商大学,浙江 杭州
收稿日期:2021年3月22日;录用日期:2021年4月11日;发布日期:2021年4月27日

摘要
本文主要用行波法来求解一类带有导数项非线性薛定谔方程的行波解。首先通过引入行波变换 ,将非线性的偏微分方程化为常微分方程组,进一步得到哈密尔顿系统,通过讨论一元三次方程根的情况对其表达式进行化简。然后借助软件求解方程,得到原方程行波解的函数解析式并结合图像,较为清晰地展现其波形。
关键词
行波法,非线性薛定谔方程,一元三次方程根的情况

Traveling Wave Solutions for a Nonlinear Schrodinger Equation with Derivative Terms
Ronghua Cheng1, Lin Xiang2*
1Yunnan University of Finance and Economics, Kunming Yunnan
2Zhejiang Gongshang University, Hangzhou Zhejiang
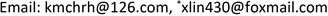
Received: Mar. 22nd, 2021; accepted: Apr. 11th, 2021; published: Apr. 27th, 2021

ABSTRACT
This paper mainly uses the traveling wave method to solve a nonlinear Schrodinger equation with derivative term for its travelling wave solutions. Firstly, one introduces a travelling wave transformation to transform the nonlinear Schrodinger equation into the ordinary differential equations; the Hamilton system is further obtained. In the process of getting the travelling wave solutions, the roots of simple Cubic Equations are discussed to simplify a Cubic expression. Then, one obtains some analytical solutions. Lastly, one presents clearly the travelling wave from the graphs of the solutions.
Keywords:Traveling Wave Method, Derivative Nonlinear Schrodinger Equation, Simple Cubic Equations

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
偏微分方程 [1] 的兴起已有两百多年的历史了,其最初的研究大部分直接来源于几何和物理中的问题,而到现在已经发展为一个独立的数学分支,其所涵括的内容复杂,求解方法多样。近几十年来,学界对该领域的研究工作,特别是对非线性方程的理论、应用及其计算方法的研究,活跃度颇高。本文考虑的是一类带有导数项非线性薛定谔方程。薛定谔方程(Schrödinger equation)又称薛定谔波动方程(Schrodinger wave equation),是由奥地利物理学家薛定谔提出的量子力学中的一个基本方程,也是量子力学的一个基本假定。这也是一个起源于物理的方程,对于不同的薛定谔方程,不少学者已探究出自己的一套解法,例如:Darboux变换法 [2],tanh函数法 [3],F展开法 [4],齐次平衡法 [5] 等。李继彬等人在文中 [6] 详述了用行波法中的动力系统方法求解偏微分方程,提供了很多的经典论述。
本文借鉴其方法思路求一类带有导数项的非线性薛定谔方程的行波解。所研究的方程为
首先引入行波变换,将方程简化为常微分方程组,进一步获得满足守恒律的哈密尔顿体系,再借助一元三次方程根的情况,得到方程的行波解。
2. 方程的行波变换
对于方程
(1)
其中 为实变量, 为未知复函数, 为实常数。
首先,引入行波变换, 其中 ,为实参数,则方程(1)可化为:
.
从而 满足以下方程
(2)式两边同乘以 ,并对 积分,取积分常数为零,有
(4)
再次对 积分,得
(5)
那么只要我们能求出 的表达式, 的表达式由此便可得。将(4)式代入(3)式,得
(6)
考虑到系数比较复杂,我们考虑较为直观较易求解的形式,取 ,由此(6)变形为
(7)
其中 。令 ,则由(7)式有 。
故哈密尔顿系统为: ,移项并整理有: ,考虑y为正,则有 ,即 ,分离变量 [7] 并积分有,
(8)
记 ,这里只考虑 。要想求解(8)式右边积分,需对 进行处理,将其化为几个低次幂项的乘积,下面将根据一元三次方程根的情况对 进行分解。
3. 方程的行波解
对于函数 ,令 能得到
(9)
作变换 ,便将方程(9)化为: ,其中 。下面根据一元三次方程根 [8] [9] 的分类讨论结果表示方程行波解的解析形式。
3.1. 且
此时方程(9)有三重实根 ,在这种情况下
,.
则有 ,积分可得: 。
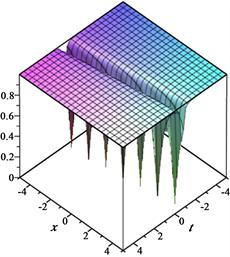
又由(5)式,则 。从而 。图像如图1所示。
 (a)
(a)
 (b)
(b)
 (c)
(c)
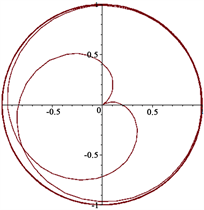
Figure 1. (a) Image of ; (b) Image of ; (c) Image of
图1. 。(a) 的图像;(b) 的图像;(c) 的图像
3.2. 而
在这种情况下方程(8)有三个实根,包含一对重根,即: (考虑 的情形), ,则在这种情况下可以得到 ,。
则有 ,积分有:
.
又由(5)式,可以得到:
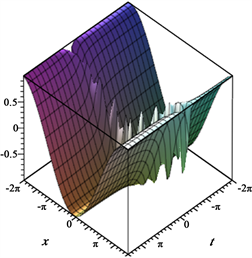
从而可求得 ,其图像如图2所示。
 (a)
(a)
 (b)
(b)
 (c)
(c)
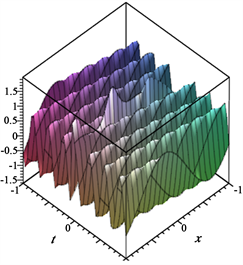
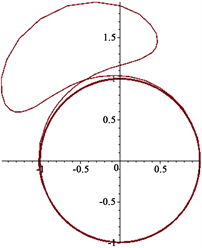
Figure 2. . (a) Image of ; (b) Image of ; (c) Image of
图2. 。(a) 的图像;(b) 的图像;(c) 的图像
3.3. (必有 )且
此时方程(9)有三个互异实根, ,则 ,。
从而 ,积分得
.
其中, 为雅可比椭圆函数的一类,它是第一类椭圆积分的反函数。
又由(5)式,但因为 的表达式太过复杂, 很难以函数表达出来。为此这里采用取特殊值的方法来探究这个函数的形式,观察其函数表达式,令 ,则 ,从而 。这里给出函数 的图像,如图3所示。
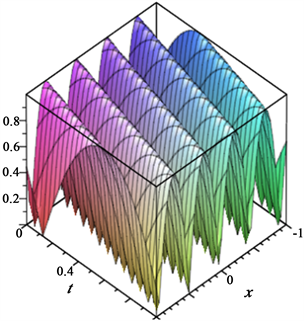
Figure 3. Image of
图3. 的图像
4. 结论
本文采用行波法中的动力系统方法求解一类导数非线性薛定谔方程,在求解过程中涉及一元三次方程的求解,借助软件,求出了该类方程的解的表达式,结合图像,展现出解的结构。由此也得见,用动力系统方法求解偏微分方程是很有效的。
基金项目
2021年云南省教育厅科研项目。
文章引用
成蓉华,项 琳. 一类带有导数项的非线性薛定谔方程的行波解
Traveling Wave Solutions for a Nonlinear Schrodinger Equation with Derivative Terms[J]. 应用数学进展, 2021, 10(04): 1103-1108. https://doi.org/10.12677/AAM.2021.104119
参考文献
- 1. 陈祖墀. 偏微分方程[M]. 第3版. 北京: 高等教育出版社, 2008: 1-10.
- 2. 蒋文丽, 程慧燕. mKP方程的达布变换与精确解[J]. 贵阳学院学报(自然科学版), 2015, 10(3): 7-9, 12.
- 3. 徐振民, 李柱. 推广的Tanh-函数法及其应用[J]. 广西民族大学学报(自然科学版), 2009, 15(3): 54-56, 87.
- 4. 刘涛立. F-展开法研究[D]: [硕士学位论文]. 兰州: 兰州大学, 2004.
- 5. 杨攀攀. 齐次平衡法和非线性偏微分方程的孤立波解[D]: [硕士学位论文]. 南京: 南京理工大学, 2008.
- 6. Li, J. (2014) Bifurcations and Exact Traveling Wave Solutions for a Model of Nonlinear Pulse Propagation in Optical Fibers. International Journal of Bifurcation and Chaos, 24, Article ID: 1450088. https://doi.org/10.1142/S0218127414500886
- 7. 钟万勰. 分离变量法与哈密尔顿体系[J]. 计算结构力学及其应用, 1999, 8(3): 229-240.
- 8. 辜青萍. 拐点和一元三次方程的求根公式[J]. 汉江大学学报(自然科学版), 2002, 19(1): 28-31.
- 9. 邢富冲. 一元三次方程求解探索[J]. 中央民族大学学报(自然科学版), 2003, 12(3): 207-218.
NOTES
*通讯作者。