Advances in Applied Mathematics
Vol.
13
No.
01
(
2024
), Article ID:
79646
,
8
pages
10.12677/AAM.2024.131031
一类病毒群体免疫最小免疫人口推断及检验
许宏飞1*,尹明智1,唐亚林2
1湖南科技学院理学院,湖南 永州
2湘潭大学数学与计算科学学院,湖南 湘潭
收稿日期:2023年12月19日;录用日期:2024年1月13日;发布日期:2024年1月23日

摘要
本文通过微分动力系统研究新冠病毒群体免疫屏障所需的最小免疫人口比率,并探究免疫人口比率对疫情爆发的影响。采用参数时变的SIR模型,通过一阶差分得到感染率和移出率的表达式,并对其进行曲线拟合。利用下一代矩阵法推导基本再生数的表达式,借助建立群体免疫屏障的临界基本再生数,确定新冠病毒群体免疫屏障所需的最小免疫人口比率。经过数值计算表明,即使随机感染率服从以原始最大感染率为均值,以0.1倍的原始最大感染率为标准差的正态分布,只要免疫人口比率不低于72.03%,人群依然能够建立起群体免疫屏障,有效控制新冠病毒的传播。这项研究的方法和结果也可以为控制其它动植物病毒提供有益的指导。
关键词
群体免疫屏障,SIR模型,基本再生数,免疫人口比率

A Class of Virus Population Immunity Minimum Immune Population Inference and Testing
Hongfei Xu1*, Mingzhi Yin1, Yalin Tang2
1School of Science, Hunan University of Science and Engineering, Yongzhou Hunan
2School of Mathematics and Computational Science, Xiangtan University, Xiangtan Hunan
Received: Dec. 19th, 2023; accepted: Jan. 13th, 2024; published: Jan. 23rd, 2024

ABSTRACT
This study investigates the minimum immune population ratio required for achieving herd immunity against the novel coronavirus and explores the impact of the immune population ratio on the outbreak of the epidemic using a differential dynamical system. The time-varying SIR model is employed, and the expressions for the infection rate and removal rate are obtained through first-order differencing and curve fitting. The expression for the basic reproduction number is derived using the next-generation matrix method. By establishing the critical basic reproduction number for achieving herd immunity, the minimum immune population ratio required for the novel coronavirus is determined. Numerical calculations demonstrate that even under the condition where the stochastic infection rate follows a normal distribution with the original maximum infection rate as the mean and 0.1 times the original maximum infection rate as the variance, as long as the immune population ratio is not lower than 72.03%, the population can still establish herd immunity and effectively control the transmission of the novel coronavirus. The methods and results of this study can provide valuable guidance for controlling other animal and plant viruses.
Keywords:Herd Immunity Barrier, SIR Model, Basic Reproduction Number, Immunization Population Ratio

Copyright © 2024 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
自2019年冬季开始,一种全球性的传染病迅速蔓延,2020年1月30日,世界卫生组织(WHO)宣布新冠病毒肺炎(SARS-CoV-2)爆发为国际紧急情况。新冠大流行成为了全球公共卫生紧急事件。截至2022年12月,全球范围内,几乎每八个人中就有一个人感染过新冠病毒,且每一百个感染者中大约有一个人死亡 [1] ,面对这高致病率高死亡率的新冠病毒,中国很快实施了严格的防疫政策,保障人民的健康,根据人类历史对抗天花等病毒的成功经验,科研和医疗单位也都紧急投入到治疗新冠病人和疫苗的研制工作中,无论是治愈新冠病人还是成功研制出疫苗,使易感染者具有对病毒的抗体,目的都是为了增大人群中移出者的比例。事实上在与新冠病毒的斗争中人们发现,彻底结束新冠疫情关键在于建立群体免疫屏障 [2] 。群体免疫屏障是一种有效控制疫情传播的策略。当足够多的人获得免疫力后,病毒在人群中的传播速度会显著降低,从而减少疫情的传播风险。建立新冠病毒的免疫屏障对于保护高风险人群至关重要,特别是那些无法接种疫苗或疫苗效果不佳的人,例如老年人和患有慢性疾病的人。当足够多的人获得免疫力后,可以为这些高风险人群提供更好的保护和安全。此外,快速建立免疫屏障还可以促进经济的恢复。疫情对经济造成了巨大的冲击,而群体免疫屏障的建立可以帮助快速结束疫情,从而加速经济的复苏。而实现群体免疫屏障只能依靠接种疫苗 [3] 。面对传染病的消极影响,人们对群体免疫屏障有许多研究。吴丹等人直接研究了群体免疫屏障对新冠传染病的意义,给出了通过自然感染建立免疫屏障的可行性和风险的定性分析 [4] 。王佳亮等人,使用小世界网络模型,模拟了新冠病毒的传播过程,仿真计算了达到群体免疫的数值 [5] 。叶红霞等人建立SEIR模型,研究了接种新冠病毒疫苗后,新冠疫情的发展趋势与控制,同时使用建立logistic模型,来预测感染人数的变化并根据疫苗接种率推算出完成免疫屏障的构建所需要的时间 [6] 。陈胤忠等人对研究了群体免疫屏障在甲型肝炎中的效果,在大面积接种甲肝疫苗后,可以阻断了甲肝流行,使发病率达到历史最低 [7] 。Pell等人建立了分布时滞传播模型,研究群体免疫屏障的建立,需要在人群中高度遵守疫苗接种规定和每年增加疫苗接种的频率 [8] 。本研究将借助基本再生数确定新冠病毒免疫屏障所需的最小免疫人口比率,并探究免疫人口比率对疫情爆发的影响。免疫屏障是指通过疫苗接种或自然感染后,人群中具有免疫力的个体达到一定比例,从而有效地抑制病毒的传播,保护整个人群免受疾病侵袭。
2. 数学模型
假设某地区总人口恒定为 ,新冠疫情发生后,多数人担忧患上新冠肺炎疾病,以及政府的及时防疫措施的影响,人口流动受阻,故不考虑人口流动,同时也不考虑自然死亡和出生等其他因素的影响,使总人口近似不变。假定考虑三类人群:易感染人群 ,已感染人群 和移出人群 ,所以 。
在建立新冠群体免疫过程中,假设三类人群在空间是均匀分布的,即每个人在单位时间接触到的人数是相同的,被感染的概率也是相同的。设 时刻,易感染者与感染者接触转变为感染者的概率为 ,感染者治愈率为 。所以时变参数的SIR模型为
(1)
由于 ,回代模型(1),可化简为
(2)
下面对参数 和 进行拟合,根据历史记录数据可以拟合出 和 与时间的关系,先求解 ,对(2)的第二个方程进行一阶差分,可得
(3)
将(2)的第一个方程进行一阶差分,并代入(3)可得
(4)
3. 群体免疫屏障模型
在流行病学中, 是指在没有外力干预并且所有人没有免疫力的情况下,某种传染病的感染者平均会传染给多少人。 的值越大,代表传染病的传染性越强,也就是说疾病更难控制 [9] [10] [11] 。采用下一代矩阵法求 [10] [11] ,模型(1)的无病平衡点为 ,关于感染者变化率的方程
既包含易感染个体到感染个体的转化量 ,也包含感染个体到移出个体的转化量 。根据文献 [10] [11] ,
, ,
那么再生矩阵为 ,所以基本再生数为
. (5)
新冠病毒群体免疫是指在某一特定社区或人群中,大多数人通过感染新冠病毒或接种疫苗后,获得对该病毒的免疫能力。这种免疫能够形成一道保护屏障,有效减少病毒的传播和疫情的爆发可能性。当足够多的人群获得免疫后,病毒在人群中的传播会受到限制,达到控制疫情的目的。
设 为获得免疫人口所占比例,易感染人口所占比例为 ,根据基本再生数的定义,当人群中出现一个感染者时,平均可以感染的人数为病毒初始基本再生数与 的乘积,要控制疫情不爆发,则必须 ,所以对新冠病毒取得群体免疫至少需要的免疫人口比率为
. (6)
4. 结果
要讨论新冠病毒的传播能力,需要研究几乎无外界干预时病毒的传播数据,因此本文选2020年1月30日至4月22日的湖北武汉每日疫情统计数据,数据来自于中华人民共和国国家健康卫生委员会官网 [12] 。根据武汉市第七次全国人口普查公报数据 [13] ,设总人数 。
代入数据计算(3)~(4)式得到 ,容易发现 的曲线具有指数特征,对 和 进行指数拟合,在拟合参数的置信区间选取
(7)
代入模型(2)进行数值计算绘出 的时间历程图,由图1可以看出拟合得到的感染率和移出率,使模型(2)对感染者群体和移出群体的变化做出较好的预测。
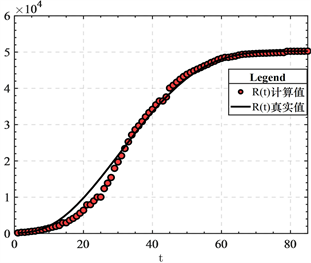
 (a) (b)
(a) (b)
Figure 1. Comparison of the calculated values of with the actual values
图1. 的计算值与真实值的比较
考虑该病毒在最少干预下,最大传播速度时的 为该病毒的基本再生数,即为 取得最大值时刻对应的 。由于 的表达式不能直接由模型(1)积分得到,利用真实数据计算 的一阶差分的最大值,绘制时间与 的一阶差分值图,见图2。容易看到在 时,病毒的传播速度最大,根据基本再生数函数(5)可得,此时系统对应的 ,即该病毒在爆发初期的基本再生数约为3.5756。因此由最小群体免疫人口比率(6)可得达到群体免疫最小的免疫人口比率为 。
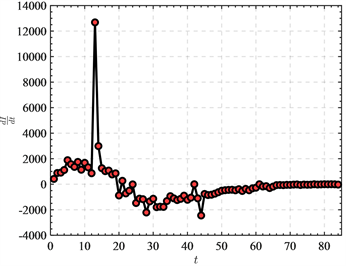
Figure 2. The first-order difference value of and
图2. 与 的一阶差分值
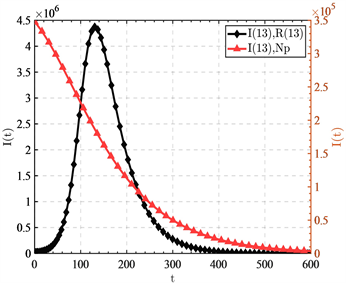
Figure 3. Infection trend graph with different immune levels but the same initial number of infected individuals
图3. 相同初始感染者量不同免疫者量下的感染趋势图
5. 免疫人口比例检验
当免疫人口比例能够实现群体免疫时,可以有效减轻医院的接诊压力,减少社会生产和生活的影响。因此有必要检验模型得到的免疫人口比率 的有效性。
双 轴图3显示了在基本再生数 达到最大时对应的系统的感染率和移出率状态下,比较原始人群在具有 量的感染者和 量的移出者时的感染趋势与具有 量的感染者和 量的免疫人口时的感染趋势。发现左侧 轴对应的曲线,原始人群的感染会快速上升达到一个顶峰,然后再下降,事实上这里的下降根据实际多为死亡移出,疫情并不是真正得到控制。而右侧 轴对应的曲线,有 量的初始免疫人口的曲线则从开始时刻就直接快速下降,直到疫情得到控制。对比发现通过接种疫苗使得人群具有 比率的免疫人口确实可以快速控制疫情。
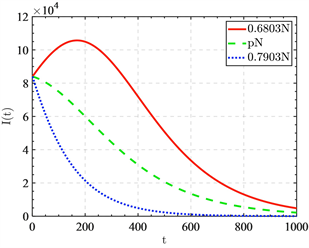
Figure 4. The change curve of with different initial immune populations
图4. 不同初始免疫人口下 的变化曲线

Figure 5. The change curve of with initial immune population under random infection rate
图5. 随机感染率下初始免疫人口下 的变化曲线
观察具有 的左右近似初始免疫人口比率的感染趋势图4,发现当免疫人口比率为 时,感染者人数会先增多,再下降,疫情有一个小峰值的爆发。当免疫人口比率为 时,感染者人数会直接下降,没有疫情的爆发。当免疫人口比率为 时,感染者人数变化曲线比免疫人口比率为 时更陡峭,下降速度更快,初始免疫人口越大,疫情会得到更快的控制。
新冠病毒在不同环境,不同年龄段人群的感染率是不完全相同的,在初始免疫人口比率为 ,与图4相同的初始感染者人数和移出率的情况下,考虑具有随机感染率的SIR模型。假设感染率以天为单位更新,感染率服从均值为 ,标准差为 的正态分布。则模型(1)以天为时间步长差分为离散动力系统
(8)
由参数拟合结果(7)和 可设随机感染率为 。对随机模型(8)做10次模拟得到图5,发现在随机感染率下,所有的感染者人数变化曲线都是具有小的振荡,不再光滑,只有少量的感染者人数变化曲线会有短暂的上升,但大部分感染者变化曲线都是伴有微小振动的下降,病毒不会继续蔓延,而是直接衰减,直至得到控制。因此模型推导得到的群体免疫的免疫人口比率为 ,在感染率受到一定的随机影响下依然有效。
6. 结论
论文建立参数时变的SIR模型,对微分方程进行一阶差分,得到参数感染率和移出率的迭代表达式。为了得到新冠病毒尽可能少的外界影响下的基本再生数,本文选择武汉2020年初的新冠病毒传播数据,采用下一代矩阵法推导基本再生数的表达式。建立群体免疫屏障时,选择实际数据取到的最大的基本再生数,以确保得到的免疫人口比率尽可能有效。根据群体免疫的定义,以使得新冠疫情不爆发的最小的免疫人口比率为新冠病毒免疫屏障所需免疫人口比率。最后,借助数值计算对得到的免疫人口比率进行不同免疫人口比率和原始人群情况的对比检验,发现免疫人口比率 情况下,新冠病毒不会爆发。对具有随机感染率的情况做了多次模拟实验,发现总体上,当人群具有免疫人口比率 情况下,新冠病毒不会蔓延传播,人群依然能够建立起免疫屏障。
基金项目
湖南省教育厅项目(21C0701),2023 年永州市指导性科技计划项目(2023YZ002),湖南科技学院科学研究项目(23XKYZZ05),湖南科技学院科学研究项目(20XKY060)。
文章引用
许宏飞,尹明智,唐亚林. 一类病毒群体免疫最小免疫人口推断及检验
A Class of Virus Population Immunity Minimum Immune Population Inference and Testing[J]. 应用数学进展, 2024, 13(01): 285-292. https://doi.org/10.12677/AAM.2024.131031
参考文献
- 1. World Health Organization (2022) WHO Coronavirus (COVID-19) Dash/Board. https://data.who.int/dashboards/covid19/data
- 2. Bhadra, S., et al. (2021) Herd Immunity: An End to the Global COVID 19 Pandemic Crises. International Research in Medical and Health Sciences, 4, 12-29.
- 3. 胡家林. 接种新冠病毒疫苗共筑健康免疫屏障[J]. 当代贵州, 2021(30): 34-35.
- 4. 吴丹, 郑徽, 李艺星, 等. 群体免疫及其对传染病防控的意义[J]. 中国疫苗和免疫, 2020, 26(4): 479-483.
- 5. 王佳亮, 李海滨, 李海燕. 基于复杂网络的新冠病毒群体免疫数值仿真[J]. 复杂系统与复杂性科学, 2023, 20(1): 27-33.
- 6. 叶红霞, 刘应辉, 吴凌逸. 基于SEIR模型对接种新冠病毒疫苗的预测与控制[J]. 哈尔滨师范大学自然科学学报, 2022, 38(2): 30-36.
- 7. 陈胤忠, 姜仁杰, 俞文祥, 等. 建立群体免疫屏障控制甲型肝炎流行的效果研究[J]. 复杂系统与复杂性科学, 2023, 20(1): 27-33.
- 8. Pell, B., Johnston, M.D. and Nelson, P. (2022) A Data-Validated Temporary Immunity Model of COVID-19 Spread in Michigan. Mathematical Biosciences and Engineering, 19, 10122-10142. https://doi.org/10.3934/mbe.2022474
- 9. Wallinga, J. and Lipsitch, M. (2007) How Generation Intervals Shape the Relationship between Growth Rates and Reproductive Numbers. Proceedings of the Royal Society B: Biological Sciences, 274. https://doi.org/10.1098/rspb.2006.3754
- 10. 崔玉美, 陈姗姗, 傅新楚. 几类传染病模型中基本再生数的计算[J]. 复杂系统与复杂性科学, 2017, 14(4): 14-31.
- 11. van den Driessche, P. and Watmough, J. (2002) Reproduction Numbers and Sub-Threshold Endemic Equilibria for Compartmental Models of Disease Transmission. Mathematical Biosciences, 180, 29-48. https://doi.org/10.1016/S0025-5564(02)00108-6
- 12. 中华人民共和国国家卫生健康委员会. 疫情通报[EB/OL]. http://www.nhc.gov.cn/xcs/yqtb/list_gzbd_41.shtml, 2020-04-22.
- 13. 武汉市统计局. 武汉市第七次全国人口普查公报[EB/OL]. https://tjj.wuhan.gov.cn/ztzl_49/pczl/202109/t20210916_1779157.shtml, 2021-09-16.
NOTES
*通讯作者。