Pure Mathematics
Vol.
09
No.
03
(
2019
), Article ID:
30411
,
7
pages
10.12677/PM.2019.93062
Proof and Matlab Simulation of the Para-Symmetry DMC Capacity
Haixia Hao*, Lei Zhang, Zijun Xu, Mei Wu
School of Mathematics, Jinzhong University, Jinzhong Shanxi

Received: Apr. 29th, 2019; accepted: May 9th, 2019; published: May 24th, 2019

ABSTRACT
Channel capacity represents the maximum capacity of the channel to transmit information. This paper introduces what is the discrete para-symmetric channel and gives the proof process of its channel capacity. Finally the calculation of channel capacity is realized by using Matlab. The results show that the channel capacity can be reached when the probability of each symbol input is equal. This conclusion is consistent with the reality and has certain reference value for the understanding of the channel theory.
Keywords:Para-Symmetry Channel, Channel Capacity, Matlab Implementation
准对称信道信道容量的证明及其Matlab实现
郝海霞*,张磊,徐子钧,武梅
晋中学院数学学院,山西 晋中

收稿日期:2019年4月29日;录用日期:2019年5月9日;发布日期:2019年5月24日

摘 要
信道容量表示信道传输信息的最大能力。本文介绍了什么是离散准对称信道,给出了其信道容量的证明过程,最后通过Matlab实现了信道容量的计算,结果表明当输入的每一个符号的概率都相等时达到信道容量,符合实际,并对加深信道理论的理解有一定的参考价值。
关键词 :准对称信道,信道容量,Matlab实现

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
信息论是关于通信的理论,是用概率统计的方法研究信息的传输、存储与处理以及如何实现其有效性和可靠性的一门学科。它包括两个基本的问题,一个是信源编码,解决信源的相关性问题,去掉冗余,从而压缩了信源输出,提高了有效性;另一个是信道编码,克服信道中的干扰和噪声,提高了可靠性。可见信道是通信系统的重要组成部分,它的任务是实现信息的传输,在信道固定的情况下,总是希望传输的信息越多越好。本文主要研究一种特殊的信道,即离散准对称信道。
2. 离散准对称信道的定义及信道容量
定义1 设有一个信道矩阵,它的每一行元素都相同,只是排列不同,它的每一列元素也都相同,只是排列不同,称该信道为对称信道。
定义2 设有一个r行s列的离散无记忆信道的信道矩阵P,根据信道的输出集Y可以将P分成n个子矩阵 ,每个子矩阵对应的信道都是对称信道,称这个信道为准对称信道 [1] 。
定义3信道容量 ,其中 为平均互信息, 为输入符号概率。
3. 离散准对称信道信道容量的证明
定理1当输入的每一个符号的概率 都相等时,达到信道容量C。
定理2 设有一个信道,它的输入符号个数有r个,输出符号个数有s个,当且仅当存在常数C使输入分布 满足:
1)
2)
时, 达极大值。此时,常数C即为所求的信道容量。
定理3当输入的每一个符号的概率 都相等时,准对称信道的容量为:
,
其中,log默认是以2为底的对数,r是信道矩阵的行数, 表示信道矩阵P中的任意一行元素, 是第k个子矩阵中行元素之和, 是第k个子矩阵中列元素之和 [2] 。
证明:设准对称信道的矩阵为
,
将矩阵P分为n个对称子阵 ,对应的输出符号集Y划分为 ,设 ,则有:
,
因为P是准对称矩阵,它的行元素由 排列而成,所以有:
,
设 ,即输入等概分布,则后一项为:
,
因为 对称,所以有:
都与 无关,
其中 为y固定时,矩阵 中列元素之和,是一个常数。
,
其中, 表示 固定时,矩阵 中行元素之和,也是一个常数。
所以有:
,
所以得到:
,
根据定理2,有:
。 (证毕)
4. Matlab实验仿真 [3] [4]
首先考虑特殊的二元信道,其输入符号概率空间,即信源概率空间为:
,
它的信道矩阵是一个对称矩阵,如下:
,
该信道的互信息量为: 。
用matlab绘制当w从0到1和p从0到1之间变化时,平均互信息 的曲线,程序代码如下:
[w,p]=meshgrid(0.00001:0.001:1);
h=-(w.*(1-p)+(1-w).*p).*log2(w.*(1-p)+(1-w).*p)-(w.*p+(1-w).*(1-p)).*log2(w.*p+(1-w).*(1-p))+p.*log2(p)+(1-p).*log2(1-p);
meshz(w,p,h);
title('平均互信息');
ylabel('H(w,p,h)')
实验结果见图1。
当p固定时(这里随机取的 ),得到固定二元对称信道的平均互信息图像,程序代码如下:
w=0.00001:0.001:1;
p=0.3;
h=-(w.*(1-p)+(1-w).*p).*log2(w.*(1-p)+(1-w).*p)-(w.*p+(1-w).*(1-p)).*log2(w.*p+(1-w).*(1-p))+p.*log2(p)+(1-p).*log2(1-p);
plot(w,h);
title('固定对称信道的平均互信息');
ylabel('1-H(p)')
实验结果见图2。
对任何一般的准对称信道的信道容量,求解它的matlab程序代码如下:
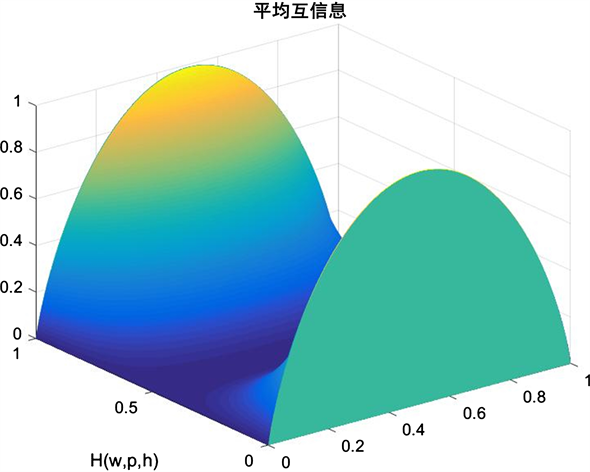
Figure 1. Average mutual information
图1. 平均互信息
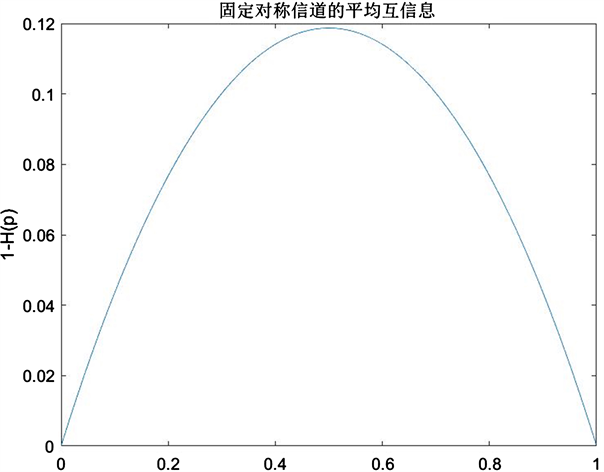
Figure 2. Average mutual information of fixed symmetric channels
图2. 固定对称信道的平均互信息
function [C,e,PX]=Channel(P)
[r,s]=size(P);
PX=(1/r)*ones(1,r);
PX_1=rand(1,r);
PX_2=PX_1/sum(PX_1);
PY=PX*P;
PY_2=PX_2*P;
[m,n]=size(PY);
HY=0;
HY_2=0;
H=0;
for i=1:n
HY=HY+PY(i)*log2(PY(i));
HY_2=HY_2+PY_2(i)*log2(PY_2(i));
end
HY=-HY;
HY_2=-HY_2;
P=P+(P==0).*eps;
for i=1:s
H=H+P(1,i)*log2(P(1,i));
end
H=-H;
PX
C=HY-H
C_2=HY_2-H;
e=C-C_2
在命令窗口输入准对称信道矩阵:
(1) P=[1/2 1/4 1/8 1/8;1/4 1/2 1/8 1/8];
[C,e,PX]=Channel(P)
仿真结果如下:
C =0.0613,e = 0.0064,PX = 0.50000.5000.
(2) P=[1/2 1/2 0 0;0 1/2 1/2 0;0 0 1/2 1/2;1/2 0 0 1/2];
[C,e,PX]=Channel(P)
仿真结果如下:
C =1.0000,e = 0.0452,PX = 0.25000.25000.25000.2500.
5. 实验结果分析
图1图像表明平均互信息 是输入概率 和信道传递概率 的函数。
图2曲线表明,当信道固定的时候, 关于 是上凸的;且当输入的每一个符号的概率都相等时,即当 时, 最大,达到信道容量C。
通过第三个实验,对于一般的准对称信道,通过Matlab结果可以看到,当对任意取的输入分布不等概时,求得的平均互信息与信道容量C的差都大于0,当输入分布PX等概时,达到信道容量C。
6. 结论
通过对准对称信道信道容量的证明及Matlab结果得到,当信源输入的每一个符号的概率都相等时,达到了信道容量。而准对称信道其实也包含了对称信道,因而也验证了对称信道的信道容量也是在输入的每一个符号概率相等时达到。通过Matlab实验也可以看出。通过对该程序代码进行改进,还可以求得任何信道的信道容量及对应的输入分布,有待进一步验证。
基金项目
网络连通性的优化研究,编号为bsjj2016202。
文章引用
郝海霞,张 磊,徐子钧,武 梅. 准对称信道信道容量的证明及其Matlab实现
Proof and Matlab Simulation of the Para-Symmetry DMC Capacity[J]. 理论数学, 2019, 09(03): 465-471. https://doi.org/10.12677/PM.2019.93062
参考文献
- 1. 周荫清. 信息理论基础[M]. 第四版. 北京: 北京航空航天出版社, 2012.
- 2. 孙杨, 杨海涛, 张亚平, 等. 关于准对称离散无记忆信道容量两个定理的等价性[J]. 内蒙古民族大学学报: 自然科学版, 2005, 20(4): 369-371.
- 3. 方飞, 余泽德. 准对称信道容量的实验仿真[J]. 实验科学与技术, 2008, 6(5): 61-62.
- 4. 徐伟业, 耿苏燕, 马湘蓉, 等. 任意DMC信道容量的计算与仿真[J]. 信息技术, 2017(6): 121-123, 128.
NOTES
*通讯作者。