Journal of Oil and Gas Technology
Vol.
41
No.
05
(
2019
), Article ID:
32887
,
5
pages
10.12677/JOGT.2019.415068
Study on Mechanical Properties of Coiled Tubing Setting Operation
Tianzeng Bai, Yongqiang Ren, Chunhua Yang, De Wu, Bo Zheng, Xiaoyong Fu
Downhole Operation Company of Bohai Drilling Engineering Company, CNPC, Renqiu Hebei

Received: Jun. 20th, 2019; accepted: Aug. 18th, 2019; published: Oct. 15th, 2019



ABSTRACT
During the operation of coiled tubings, great influence would be induced because of the internal and external pressure of downhole fluid, tubing instability and bending as well as other factors. Based on the well depth coordinate parameters of drilling rig, the geometric model of well trajectory was established, and the numerical integration method of Simpson quadrature formula was used to calculate the well shaft coordinate parameters. Based on the obtained coordinate parameters, the mechanical properties of coiled tubing, such as annulus pressure, axial force and bending moment, were analyzed and calculated respectively. Based on the actual borehole trajectory parameters, the mechanical properties were analyzed with each equation. It provides a basis for analyzing the mechanical properties of coiled tubings.
Keywords:Coiled Tubing, Well Trajectory, Mechanical Property, Numerical Integration Method
连续油管下入作业力学特性研究
白田增,任勇强,杨春华,吴德,郑博,傅小勇
渤海钻探工程有限公司井下作业分公司,河北 任丘
作者简介:白田增(1967-),男,高级工程师,主要从事井下作业工程等方面的工作。

收稿日期:2019年6月20日;录用日期:2019年8月18日;发布日期:2019年10月15日

摘 要
连续油管在作业过程中,井下液体内外压及油管失稳弯曲等因素对连续油管造成极大影响。基于钻机作业下的井深坐标参数,建立井眼轨迹几何模型,采用复化辛普森求积公式的数值积分方法计算出井眼轴坐标参数;求解出的坐标参数,分别对连续油管的环空压力、轴向力及弯矩等连续油管力学特性进行分析计算。该研究为连续油管提供了力学分析基础。
关键词 :连续油管,井眼轨迹,力学特性,数值积分方法

Copyright © 2019 by author(s), Yangtze University and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
1. 前言
连续油管具有成本低廉、作业方便,可靠性高等特点,被广泛应用于油气田勘探开发作业各个领域。在油气开发作业中,井下液体内外压及油管失稳弯曲等因素严重影响连续油管作业的安全性与可靠性 [1] [2]。笔者基于实际连续油管相关研究,对连续油管下入作业中的力学特性进行研究。
2. 连续油管下入分析模型建立
利用任意井深坐标参数建立井眼轴线轨迹几何模型并绘制井眼轨迹和计算连续油管下入过程的载荷,通过数值积分方法 [3] [4],求得各点坐标的坐标参数,得出井眼轴坐标参数。
已知任意井的井深坐标参数(井深、井斜、方位角),绘制其3维井眼轨迹。将对应井深坐标参数的3维井眼轨迹曲线进行拟合,对整体井眼轨迹拟合曲线进行等步长划分,共划分出n个节点,对节点依次编号,取其中第i个节点作为分析对象,其下一个节点编号对应为i + 1。基于3维井眼轨迹曲线建立直角坐标系(图1),坐标原点为井眼轨迹起点即井口位置。取井眼轨迹上任意微元段为研究对象,长度为dL,与z轴夹角为井斜角1,该微元段在xoy平面的投影长度记为dH,其与y轴夹角为方位角 。
根据几何关系,得到如下关系式:
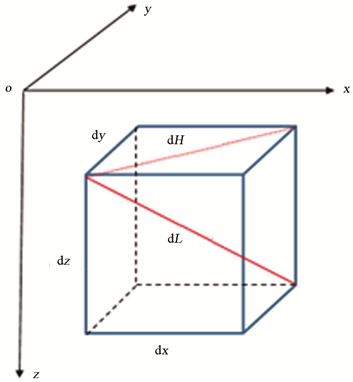
Figure 1. The micro-elemental model of well trajectory
图1. 井眼轨迹微元模型
(1)
由于坐标原点为井眼轨迹起点,因此井口位置边界条件为: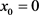 ,
,,
,
,,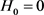 。任意井深L处的坐标参数关系式为:
。任意井深L处的坐标参数关系式为:
(2)
基于上述关系式,对于已知井斜角、方位角等井眼轨迹参数,可以得出任意井的任意点坐标参数,为后续连续油管下入分析建立数值基础。
3. 连续油管力学性能研究
3.1. 连续油管内外流体压力计算
连续油管的压力计算可用于连续油管的强度校核和管内流体计算,也可判断内外压力对连续油管强度的影响,指导连续油管安全性能评估。依照上述节点的坐标参数,对于任意连续油管节点i处内外压的差分方程其关系式为 [5]:
(3)
(4)
式中:p1、p2 为对应节点处连续油管的内、外流体的压力,Pa; 、 为对应节点处内、外流体的密度,kg/m3; 、 为对应节点处内、外流体的流速,m/s; 、 为相应节点处内、外流体的无因次黏滞摩阻系数,1; 为连续油管第i单元的长度 ,m; 为连续油管内径,mm; 为油管等效环空水力半径,m。
3.2. 连续油管轴向力计算
通过求解连续油管轴向力,可以计算出任意节点处的无因次轴力,得到连续油管在任意节点处的无因次正压力,用以判断油管在下入过程中是否会发生屈曲。
基于微元体物理方程,可以得到任意节点处的等效轴向力方程 [6]:
(5)
式中: 为对应节点处的等效轴向力,N; 为连续油管节点单元的单位长度重量,N; 为节点单元与井壁或套管壁之间的库仑摩擦系数,1; 、 为对应节点的内、外壁黏滞摩阻力,N/m。
真实轴力的计算公式为:
(6)
式中: 为对应节点处的真实轴力,N; 、 分别为连续油管任意节点处的内圆和外圆的截面积,mm2。
3.3. 连续油管弯矩计算
通过计算连续油管任意一点弯矩,可以判断连续油管是否出现弯矩过大,指导连续油管安全评估。
计算任意节点处弯矩的关系式为 [7]:
(7)
式中: 为井眼轨迹对应节点曲率,1/m;E为连续油管对应材料的弹性模量,Pa;I为截面的惯性矩,mm4; 为轴线与套管内壁轴线的距离,mm;b为量纲一的轴力,1;M为弯距,N∙mm。
4. 结语
1) 根据钻机作业下的井深坐标参数,建立井眼轨迹几何模型,对井斜角、方位角函数简单的情况直接积分计算;当函数较为复杂时,可以采用复化辛普森求积公式的数值积分方法计算井眼轴坐标参数。
2) 对于已知井眼轴坐标参数的情况下,由环空压力、轴向力、弯矩等力学特性计算公式,可以求得任意井对应节点处的力学特性,为连续油管作业提供力学分析基础。
基金项目
中国石油天然气集团公司重大工艺研究项目“华北油田套损套变井连续油管修井工艺技术研究”(2018ZD21Y-03)。
参考文献
[1] 王鹏, 王凤山, 张倩. 连续油管压裂管柱轴向载荷传递规律研究[J]. 石油矿场机械, 2016, 45(1): 20-23.
[2] 陈刚, 杨雪, 潘保芝, 等. 井眼轨迹计算及可视化研究现状[J]. 世界地质, 2015, 34(3): 830-841.
[3] 魏微. 复杂结构井井眼轨迹三维可视化技术研究[D]: [硕士学位论文]. 西安: 西安石油大学, 2012.
[4] 赵明炎. 水平井油套合压管柱力学分析[D]: [硕士学位论文]. 大庆: 东北石油大学, 2017.
[5] 程文. 连续油管力学特性分析与疲劳寿命研究[D]: [硕士学位论文]. 成都: 西南石油大学, 2016.
[6] 肖晖. 连续油管力学行为及低周疲劳寿命研究[D]: [硕士学位论文]. 成都: 西南石油大学, 2017.
[7] 张洪伟. 连续油管力学分析[D]: [硕士学位论文]. 青岛: 中国石油大学, 2010.
[编辑] 帅群