Operations Research and Fuzziology
Vol.
13
No.
02
(
2023
), Article ID:
63988
,
10
pages
10.12677/ORF.2023.132074
基于神经网络的模糊半参数回归模型
蒋珂利*,陆秋君
上海理工大学理学院,上海
收稿日期:2023年2月24日;录用日期:2023年4月7日;发布日期:2023年4月17日

摘要
本文把样条基和BP (Back Propagation)神经网络的基本原理结合起来,从而提出了一种具有模糊输入和模糊输出的自适应模糊半参数回归模型。对于所提出的自适应模糊回归模型较好地解释了模型的内在依赖性和模糊性。文中借助截断幂基作为模型的一部分,然后与非参数部分结合构造半参回归模型。利用BP神经网络预测模型中的观测输出值,然后利用LR-型模糊数的交叉验证准则和基于绝对偏差的距离测度。通过求解光滑函数、光滑函数的光滑参数带宽和回归模型的未知系数,实现了构造自适应模糊半参数回归的目标函数优化问题。通过实例并计算模型的拟合度表明所提出的模型的有效性,该策略也显著提高了所提出算法的拟合优度,并为模糊回归模型提供了数值不确定性之间的依赖框架。
关键词
LR-型模糊数,样条基,自适应模糊回归,BP神经网络,模糊半参数回归

Fuzzy Semi-Parametric Regression Model Based on Neural Networks
Keli Jiang*, Qiujun Lu
College of Science, University of Shanghai for Science and Technology, Shanghai
Received: Feb. 24th, 2023; accepted: Apr. 7th, 2023; published: Apr. 17th, 2023

ABSTRACT
In this paper, based on spline basis and BP (Back Propagation) neural network, an adaptive fuzzy semi-parametric regression model with fuzzy input and fuzzy output is presented. The intrinsic dependence and fuzziness of the adaptive fuzzy regression model are explained well. In this paper, the truncated spline basis is used as a part of the model, and then combined with the non-parametric part to construct a semi-parametric regression model. The BP neural network is used to predict the observed output values in the model, and then the cross validation criterion of LR-type fuzzy numbers and the distance measure based on absolute deviation are used. By solving the smooth function, the smooth parameter bandwidth of the smooth function and the unknown coefficient of the regression model, the objective function optimization problem of constructing adaptive fuzzy semi-parametric regression is realized. The effectiveness of the proposed model is demonstrated by an example and the fitting degree of the model is calculated. The proposed strategy also significantly improves the goodness of fit of the proposed algorithm, and provides a dependency framework for the fuzzy regression model between the numerical uncertainties.
Keywords:LR-Type Fuzzy Number, Spline Basis, Adaptive Fuzzy Regression, BP Neural Networks, Fuzzy Semi-Parametric Regression

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
回归分析 [1] 采用统计方法研究变量之间的相关性。然而,由于数据不精确,观测数据与相应的估计值之间存在偏差。因此提出一种模糊回归方法来模拟变量之间的关系。在经济系统、社会系统、工程系统、环境系统等领域也有广泛的应用,在这些领域,人类主观判断的模糊性会产生影响 [2] [3] [4] [5] 。
Tanaka et al. [6] 最早提出了模糊线性回归问题。他们最小化了系统的模糊性,以估计回归模型的参数。Lee和Chen [7] 利用广义模糊线性函数建立了广义模糊回归模型,并提出了一种非线性规划模型来识别模糊参数。之后又有Hojati et al. [8] ,Chen et al. [9] ,Spiliotis et al. [10] 等对模糊线性回归模型进行研究。Diamond [11] 研究了模糊回归建模中未知参数的最小二乘估计方法。Xu和Li [12] 开发了一个模糊类比,并用最小二乘方法处理了模糊多变量线性回归问题。一些作者对这种方法进行了研究和改进(参见示例 [13] [14] [15] )。
对于许多实际问题,输入和输出之间的函数形式往往是未知的。因此,一些研究人员提出了使用涉及神经网络的非参数模糊回归方法。Ishibuchi和Tanaka [16] 是结合模糊回归分析和反向传播神经网络来拟合区间值模糊数的上界和下界的先驱。Dunyak和Wunsch [17] 研究广义线性和非线性模糊回归分析,使用具有一般模糊数输入、输出、权重和偏差的神经网络模型。Zhang等 [18] 将模糊径向基函数网络应用于模糊非线性回归分析。He et al. [19] 使用随机权重网络开发了梯形模糊数的模糊非线性回归模型。Prakaash和Sivakumar [20] 利用一种基于递归神经网络的优化机器学习算法,结合模糊分类器和模糊回归模型,实现了一种新的数据预测系统。
除了神经网络算法,还有其他非参数技术来改进模糊回归。Cheng和Lee [21] 模糊化了应用于模糊回归方程的非参数回归技术k-最近邻和核平滑。Wang等人 [22] 提出了一个基于加权最小二乘和局部线性平滑技术的非参数模糊回归模型。Chachi等 [4] 提出了一种基于非参数多元自适应样条回归方法的模糊回归模型。注意,作为一种完全非参数的方法,它通常会导致一些缺点,如维数问题、解释困难和缺乏外推能力。值得注意的是,模糊半参数回归模型比相应的模糊非参数回归模型更具优势和灵活性。Hesamian et al. [23] 提出了一种基于曲线拟合方法和最小绝对偏差的混合方法来研究具有模糊输入、输出、平滑函数和非模糊系数的半参数部分线性模型。Akbari和Hesamian [24] 将采用半参数方法和弹性网的多元线性回归模型扩展到模糊解释变量和模糊响应变量中。
在之前的研究中,他们没有研究半参数技术和神经网络同时对自适应模糊回归模型中响应变量中心的影响。本文利用半参数回归技术、样条基和神经网络方法对线性自适应模糊回归模型进行了扩展。采用基于交叉验证准则最小化的算法选择最优带宽,采用以总距离误差最小化为目标的优化模型确定模糊回归系数。然后,通过比较我们在一些常见的拟合优度标准方面的结果来检验所提出方法的有效性和优点。
本文的其余部分组织如下。第2节回顾了LR-型模糊数、线性自适应模糊回归模型和模糊半参数部分线性模型的基本知识。第3节描述了所提出的自适应模糊半参数回归模型。然后,介绍了不同模型的性能标准,来评估所提出模型的拟合效果。在第4节中,我们进行了一些比较研究,以证明所提出模型的有效性。最后,在第5节中,我们对目前的工作作了一些总结,以供进一步研究。
2. 预备知识
本节将介绍LR-型模糊数、线性自适应模糊回归模型和模糊半参数部分线性模型的基本概念。
2.1. LR-型模糊数
LR-型模糊数 由其隶属度函数定义 [25] ,使
(1)
它完全由中心值 ,左右展值 ,严格递减左右形状函数 ,且 组成。可以表示为 。三角形模糊数 是一个LR-型模糊数,其形状函数由 定义,记为 。
Kelkinnama和Taheri [26] 定义了一个基于LR-型模糊数之间绝对偏差的距离,如下所示:
(2)
这里, , 。
2.2. 线性自适应模糊回归模型
我们考虑 ,设 是解释变量, 是响应变量 。那么线性自适应模糊回归模型的形式为 [27] :
(3)
这里, , 和 分别表示第i个输出的中心、左展和右展; , 和 是关于中心的回归模型的系数;u,v,g和z是关于左右展形的回归模型的系数; , 和 分别表示中心、左展和右展的残差。
2.3. 模糊半参数部分线性模型
给定n个的模糊观测数据 ,可以建立模糊半参数部分线性模型 [23] :
(4)
其中, 是一个待估计的实数; 是一个协变量,且 , ( ); , 是未知的光滑函数; 是一个均值为零的随机误差。
3. 建立模型
在本节中,考虑了基于样条基和神经网络的具有LR-型模糊输入和LR-型模糊输出的自适应模糊半参数回归模型。并给出了模型的计算过程和评价指标。
3.1. 基于神经网络的自适应模糊半参数回归模型
假设,我们有一组观测数据 ,其中 , , 。我们考虑以下应用d阶截断幂基的自适应模糊半参数回归模型:
(5)
其中, , , , , , ,u,v,g和z是模型中的未知系数; , 和 分别是关于解释变量中心、左展和右展的节点; , 和 表示残差; 是未知的光滑函数; 是协变量。该模型基于三个子模型。第一个子模型是模糊输出中心的估计,其他两个子模型是在第一个模型的基础上得到的。在这个公式中考虑了估计的中心与展形可能的关系,因为这在实际情况中经常是必要的。
由Nadaraya-Watson [28] ,我们可以估计未知的光滑函数 :
(6)
其中 和 为核函数 的带宽。
将(6)式代入(5)核心回归模型中的对应项,得到
(7)
神经网络可以分为前向神经网络和反馈神经网络。本文重点介绍前向神经网络的BP神经网络。BP神经网络是一种学习误差的反向传播算法。它包括两个过程:信息的正向传播和误差的反向传播。输入信号从输入层经过隐藏层到输出层。每一层神经元的状态只影响下一层神经元的状态。当输出层未达到预期输出时,将进行反向传播,并可根据预测误差调整网络的权值和偏差,从而达到BP神经网络预测输出不断接近预期输出的目的。按照以下步骤训练BP神经网络:1) 初始化神经网络2) 计算隐含层输出3) 计算输出层输出4) 计算误差5) 计算权值判断算法迭代是否结束。如果没有,请返回2)。BP神经网络在预测方面应用非常广泛。本文采用的是3层网络,即输入层,隐藏层,和输出层,如图1所示。BP神经网络方法能更准确地拟合预测趋势,预测结果更稳定。我们考虑如图1所示的三层BP神经网络。设一组输入数据为 ,输出值为 ,因此,利用样条基和BP神经网络我们可以拟合自适应模糊半参数回归模型。
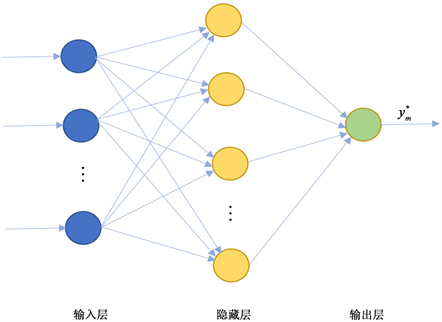
Figure 1. Structure of three-layer BP neural network
图1. 三层BP神经网络结构
设 , , , , , 。因此,将(7)中的 替换为BP神经网络计算的 ,则基于样条基和BP神经网络的自适应模糊半参数回归模型为:
(8)
3.2. 估计未知参数的方法
对于光滑函数中的光滑参数带宽h的作用是为了调整估计的平滑程度。偏小h使 波动过大,导致过拟合,偏大h使 过于平滑,无法跟踪模糊回归函数中心的潜在趋势,导致拟合不足。因此,在局部平滑技术中,选择合适的光滑参数值是非常重要的。统计学中选择最优光滑参数值的常用方法有交叉验证、广义交叉验证和Bootstrap方法。本文采用交叉验证方法中的留一法,也就是将整个数据集中的一个观测值作为验证数据集,其余观测值作为训练数据集。验证过程不断重复,直到整个数据集的每个观察结果都被用作一次验证数据集。根据绝对误差距离,光滑参数h的确定如下:
, (9)
其中, 表示去掉第i个样本之后 的估计值。对于选定的h值,如果估计的某个模糊数的左展形或右展形为负,处理这个问题的一种方法是D’urso (2003) [27] 中建议的,将负展形设置为零。
接下来是对回归模型中未知系数的估计。模糊回归系数的估计本文是通过将实际输出 值与估计输出 值之间的绝对误差最小化得到:
(10)
针对上述优化问题,本文提出了以下算法来寻找带宽和回归系数的最优值:
1) 基于BP神经网络计算 ;
2) 选择一个核函数,并根据(9)计算最优带宽;
3) 通过将(10)最小化估计模型的系数。
3.3. 模型评价
假设 和 分别是实际输出和基于所研究模型的估计输出。由 [29] 定义误差均值(ME)
(11)
其中,积分只在包含模糊数支撑的区间内计算。两个模糊数的差值越小,ME值越接近于零,模型的精度越高。但是,当观测值和预测值不重叠时,无论观测值和估计值之间的距离有多远,这种性能度量的值都是相同的。
描述响应变量的估计值隶属函数与观测值隶属函数之间的差值的拟合指标。
(12)
此外,这里还有一个拟合指标
(13)
其中G反应模糊响应变量与其模糊估计值有多接近。
此外,相似度的均值(MSM)表示如下:
(14)
其中min和max算子用于两个模糊集的交和并。当MSM较大时,模糊回归模型的预测输出与实际输出更接近。因此,MSM越大,说明对应的模糊回归模型在相似度上越好。
4. 实证分析
在本节中,我们通过一个例子来检验所提模型的可行性和有效性。我们可以令 。平滑函数是triweight核函数。
在100个样本上,我们从模型i中模拟了一个模糊输出变量和两个模糊输入变量 ,如下所示:
模型:
其中, 和 是输入观测中心样本; 为观测输入左展样本; 为观测输入右展样本。残差为 和 ; 和 是在 上观测到的随机样本。 , , 。
然后,我们将建立的模型拟合1000次,以研究我们提出的模型的性能。我们将我们的自适应模糊半参数回归与D’Urso和Gastaldi [30] ,D’Urso [27] 和Hesamian et al. [23] 给出的模型进行比较。拟合优度的均值见表1。图2描述了输出中心值与输入中心值之间的图形依赖关系。
Table 1. Fitting performance of fuzzy regression model
表1. 模糊回归模型的拟合性能
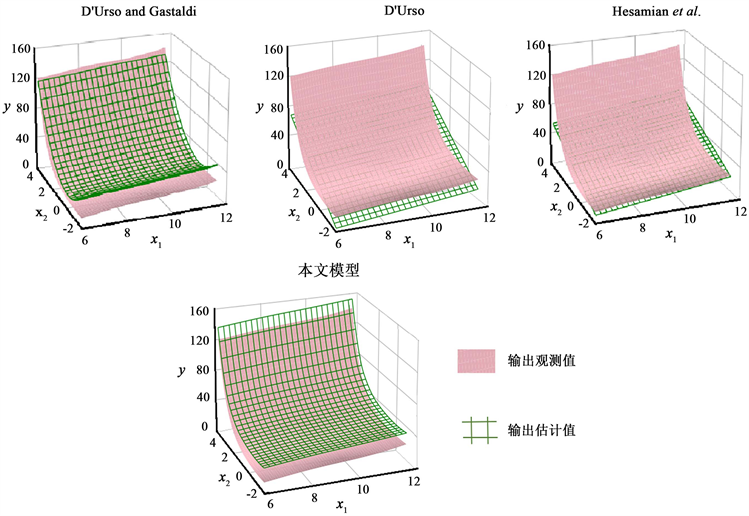
Figure 2. Comparison of observed and estimated central values of response variables
图2. 响应变量的观测中心值与估计中心值的比较
表1和图2表明,与其他三种模型相比,所提出的模型在模型拟合上得到了更好的结果,并且在输出中心值与输入中心值的依赖关系上产生了很小的偏差。
5. 结论
利用神经网络和样条基函数,研究了一种模糊输入、模糊输出的自适应模糊半参数回归模型。首先定义了自适应模糊回归模型,并结合半参数技术、样条基和BP神经网络进行了研究。然后,通过与一些经典方法的比较,讨论了我们的结果。
本文创新点在于将半参数技术和神经网络融入到自适应模糊回归模型中,相较于其他模型,本文模型的预测精度更高。根据所获得的结果,进一步的工作可以将模糊逻辑回归发展到模糊半参数回归模型中并与迭代算法结合。对于本文所建立的模型,当解释变量变多时,模型结构更为复杂,模型更加冗长,可以考虑简化模型结构。实际问题中获取的数据可能存在异常,预估的模型结果与实际会存在偏差,可以考虑更为稳健的神经网络减少异常值的干扰。
致谢
在此,我要感谢陆老师为改进这篇论文提出宝贵意见。
基金项目
本文由上海市重点学科项目资助,项目编号为No. T0502和沪江基金资助,项目编号为No. B14005。
文章引用
蒋珂利,陆秋君. 基于神经网络的模糊半参数回归模型
Fuzzy Semi-Parametric Regression Model Based on Neural Networks[J]. 运筹与模糊学, 2023, 13(02): 724-733. https://doi.org/10.12677/ORF.2023.132074
参考文献
- 1. Thrane, C. (2019) Applied Regression Analysis. Taylor and Francis, New York. https://doi.org/10.4324/9780429443756
- 2. Bardossy, A., Bogardi, I. and Duckstein, L. (1990) Fuzzy Re-gression in Hydrology. Water Resources Research, 26, 1497-1508. https://doi.org/10.1029/WR026i007p01497
- 3. Takemura, K. (2005) Fuzzy Least Squares Regression Anal-ysis for Social Judgment Study. Journal of Advanced Intelligent Computing and Intelligent Informatics, 9, 461-462. https://doi.org/10.20965/jaciii.2005.p0461
- 4. Chachi, J., Taheri, S.M. and Arghami, N.R. (2014) A Hybrid Fuzzy Regression Model and Its Application in Hydrology Engineering. Applied Soft Computing, 25, 149-158. https://doi.org/10.1016/j.asoc.2014.09.010
- 5. Tzimopoulos, C., Papadopoulos, K. and Papadopoulosc, B. (2016) Fuzzy Regression with Applications in Hydrology. Optimization, 5, 69-75.
- 6. Tanaka, H., Uejima, S. and Asai, K. (1982) Linear Regression Analysis with Fuzzy Model. IEEE Transactions on Systems, Man and Cybernetics, 12, 903-907. https://doi.org/10.1109/TSMC.1982.4308925
- 7. Lee, H.T. and Chen, S.H. (2001) Fuzzy Re-gression Model with Fuzzy Input and Output Data for Manpower Forecasting. Fuzzy Sets and Systems, 119, 205-213. https://doi.org/10.1016/S0165-0114(98)00382-0
- 8. Hojati, M., Bector, C.R. and Smimou, K. (2005) A Simple Method for Computation of Fuzzy Linear Regression. European Journal of Operational Research, 166, 172-184. https://doi.org/10.1016/j.ejor.2004.01.039
- 9. Chen, F., Chen, Y., Zhou, J., et al. (2016) Optimizing H Value for Fuzzy Linear Regression with Asymmetric Triangular Fuzzy Coefficients. Engineering Applications of Artificial Intelligence, 47, 16-24. https://doi.org/10.1016/j.engappai.2015.02.011
- 10. Spiliotis, M., Angelidis, P. and Papadopoulos, B. (2020) A Hybrid Probabilistic Bi-Sector Fuzzy Regression Based Methodology for Normal Distributed Hydrological Variable. Evolving Systems, 11, 255-268. https://doi.org/10.1007/s12530-019-09284-7
- 11. Diamond, P. (1988) Fuzzy Least Squares. Information Sciences, 46, 141-157. https://doi.org/10.1016/0020-0255(88)90047-3
- 12. Xu, R. and Li, C. (2001) Multidimensional Least-Squares Fitting with a Fuzzy Model. Fuzzy Sets and Systems, 119, 215-223. https://doi.org/10.1016/S0165-0114(98)00350-9
- 13. Nasrabadi, E. and Hashemi, S.M. (2008) Robust Fuzzy Regression Analysis Using Neural Networks. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 16, 579-598. https://doi.org/10.1142/S021848850800542X
- 14. Salmani, F., Taheri, S.M., Yoon, J.H., et al. (2017) Logistic Regression for Fuzzy Covariates: Modeling, Inference, and Applications. International Journal of Fuzzy Systems, 19, 1635-1644. https://doi.org/10.1007/s40815-016-0258-x
- 15. Gao, Y. and Lu, Q. (2018) A Fuzzy Logistic Regression Model Based on the Least Squares Estimation. Computational and Applied Mathematics, 37, 3562-3579. https://doi.org/10.1007/s40314-017-0531-0
- 16. Dunyak, J.P. and Wunsch, D. (2000) Fuzzy Regression by Fuzzy Number Neural Networks. Fuzzy Sets and Systems, 112, 371-380. https://doi.org/10.1016/S0165-0114(97)00393-X
- 17. Ishibuchi, H. and Tanaka, H. (1992) Fuzzy Regression Analysis Using Neural Networks. Fuzzy Sets and Systems, 50, 257-265. https://doi.org/10.1016/0165-0114(92)90224-R
- 18. Zhang, D., Deng, L. and Cai, K.Y. (2005) A Fuzzy Nonlinear Regression with Fuzzified Radial Basis Function Network. IEEE Transactions on Fuzzy Systems, 13, 742-760. https://doi.org/10.1109/TFUZZ.2005.859307
- 19. He, Y., Wei, C., Long, H., et al. (2018) Random Weight Network-Based Fuzzy Nonlinear Regression for Trapezoidal Fuzzy Number Data. Applied Soft Computing, 70, 959-979. https://doi.org/10.1016/j.asoc.2017.08.006
- 20. Prakaash, A.S. and Sivakumar, K. (2021) Op-timized Recurrent Neural Network with Fuzzy Classifier for Data Prediction Using Hybrid Optimization Algorithm: Scope towards Diverse Applications. International Journal of Wavelets, Multiresolution and Information Processing, 19, Article ID: 2050074. https://doi.org/10.1142/S0219691320500745
- 21. Cheng, C.B. and Lee, E.S. (1999) Nonparametric Fuzzy Regression—k-NN and Kernel Smoothing Techniques. Computers and Mathematics with Applications, 38, 239-251. https://doi.org/10.1016/S0898-1221(99)00198-4
- 22. Wang, N., Zhang, W. and Mei, C. (2007) Fuzzy Non-Parametric Regression Based on Local Linear Smoothing Technique. Information Sci-ences, 177, 3882-3900. https://doi.org/10.1016/j.ins.2007.03.002
- 23. Hesamian, G., Akbari, M.G. and Asadollahi, M. (2017) Fuzzy Semi-Parametric Partially Linear Model with Fuzzy Inputs and Fuzzy Outputs. Expert Systems with Applications, 71, 230-239. https://doi.org/10.1016/j.eswa.2016.11.032
- 24. Akbari, M.G. and Hesamian, G. (2017) A Partial-Robust-Ridge-Based Regression Model with Fuzzy Predictors-Responses. Journal of Computational and Applied Mathematics, 351, 290-301. https://doi.org/10.1016/j.cam.2018.11.006
- 25. Zimmermann, H.J. (2011) Fuzzy Set Theory and Its Applica-tions. Springer Science & Business Media, New York.
- 26. Kelkinnama, M. and Taheri, S.M. (2012) Fuzzy Least-Absolutes Regression Using Shape Preserving Operations. Information Sciences, 214, 105-120. https://doi.org/10.1016/j.ins.2012.04.017
- 27. D’Urso, P. (2003) Linear Regression Analysis for Fuzzy/Crisp Input and Fuzzy/Crisp Output Data. Computational Statistics and Data Analysis, 42, 47-72. https://doi.org/10.1016/S0167-9473(02)00117-2
- 28. Cai, Z. (2001) Weighted Nadaraya-Watson Regression Estimation. Statistics & Probability Letters, 51, 307-318. https://doi.org/10.1016/S0167-7152(00)00172-3
- 29. Kim, B. and Bishu, R.R. (1998) Evaluation of Fuzzy Linear Regression Models by Comparing Membership Functions. Fuzzy Sets and Systems, 100, 343-352. https://doi.org/10.1016/S0165-0114(97)00100-0
- 30. D’Urso, P. and Gastaldi, T. (2002) An “Orderwise” Polynomial Regression Procedure for Fuzzy Data. Fuzzy Sets and Systems, 30, 1-19. https://doi.org/10.1016/S0165-0114(02)00055-6
NOTES
*通讯作者。
