一类参数式李氏卵形曲线 A Kind of Parametric Li’s Oval Curve

doi:10.12677/AAM.2021.101036

Advances in Applied Mathematics
Vol. 10 No. 01 ( 2021 ), Article ID: 40114 , 17 pages
10.12677/AAM.2021.101036

一类参数式李氏卵形曲线

李湘江

●How to Cite this Article

长沙理工大学工程训练中心，湖南长沙

收稿日期：2020年12月25日；录用日期：2021年1月19日；发布日期：2021年1月28日

摘要

本文给出李氏卵形曲线和李氏卵圆及李氏心脏线的定义，提出一类参数式方程，证明其在一定条件下可为李氏卵形曲线、李氏卵圆及李氏心脏线。并获得了这类卵形曲线的面积、周长、质心坐标、转动惯量、旋转卵形体的体积等重要公式。

关键词

李氏卵形曲线，李氏卵圆，李氏心脏线，参数式卵形曲线方程，卵心，长半径，短半径，对称半径

A Kind of Parametric Li’s Oval Curve

Xiangjiang Li

Engineering Training Center, Changsha University of Science & Technology, Changsha Hunan

Received: Dec. 25^th, 2020; accepted: Jan. 19^th, 2021; published: Jan. 28^th, 2021

ABSTRACT

In this paper, the definitions of Li’s oval curve, Li’s oval and Li’s cardioid are given; a kind of parametric equation is proposed, which is proved to be Li’s oval, Li’s Oval circle and Li’s cardioid under certain conditions. The important formulas of the area, circumference, centroid coordinate, moment of inertia and volume of rotating oval ball are calculated.

Keywords:Li’s Oval Curve, Li’s Oval, Li’s Cardioid, Parametric Oval Equation, Oval Center, Long Radius, Short Radius, Symmetric Radius

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

笔者在文 [1] 中给出了李氏卵圆及其相关概念的定义，并提出了一类四次李氏卵圆方程，本文在此基础上给出李氏卵形曲线、李氏卵圆及李氏心脏线的定义，而把李氏卵圆作为李氏卵形曲线的一种特殊情形包括在李氏卵形曲线中，同时发现并证明一类参数式方程为李氏卵形曲线，并获得了这类卵形曲线的面积、周长、质心坐标、转动惯量、旋转卵形体的体积等重要公式。

2. 定义

定义1：平面曲线L，若满足如下条件：

① L有一条对称轴且是闭合的；

② L上有唯一一对对称点，设为S，T到对称轴的距离最大；

③ L与其对称轴有且仅有两个交点，设为P，Q，又PQ与ST交于一点设为O，且 $O P > O Q$ ；

④ L处处光滑，或者L上除点P，Q外处处光滑；

则称曲线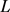为李氏卵形曲线，称点O为李氏卵形曲线的卵心，分别称点P，Q为李氏卵形曲线的远端点和近端点，称点S，T为李氏卵形曲线的对称端点，称PQ的中点 $O^{'}$ 为李氏卵形曲线的轴心，过 $O^{'}$ 作对称轴的垂线交李氏卵形曲线于 $S^{'}$ 和 $T^{'}$ ，分别称线段OP，OQ，OS (或OT)， $O^{'} Q$ (或 $O^{'} P$ )， $O^{'} S^{'}$ (或 $O^{'} T^{'}$ )， $O O^{'}$ 为李氏卵形曲线的长半径、短半径、对称半径、轴半径、次对称半径、偏心距，其长度分别记为a，b，c，e，g，h，并把正数a，b，c (a > b)称为李氏卵形曲线的三个特征参数，而把a，b，c，e，g，h称为李氏卵形曲线的六个元素。

定义2：凸的且处处光滑的李氏卵形曲线称为李氏卵圆。

定义3：仅在近端点处向里凹进去的李氏卵形曲线称为李氏心脏线。

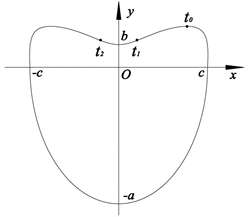
若取李氏卵形曲线的卵心作坐标系原点，近端点方向作为y轴的正向，则李氏卵形曲线在直角坐标系的示意图如图1所示。

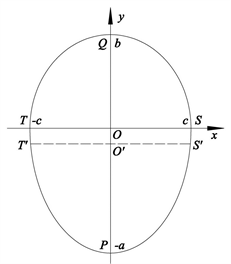
Figure 1. Li’s Oval curve and its rectangular coordinate system

图1. 李氏卵形曲线及其在直角坐标系示意图

3. 一类参数式李氏卵形曲线方程

定理1：设参数式方程

${\begin{cases} x = c \cos t \\ y = \frac{1}{2} [(a + b) - (a - b) \sin t] \sin t \end{cases}, t \in [- \frac{π}{2}, \frac{3 π}{2}]$ (3.1)

(i) 若

$a, b, c > 0$ 且 $a > b$ (3.2)

则方程(3.1)是以 $a, b, c$ 为长、短、对称半径的李氏卵形曲线方程。

(ii) 若

$a, b, c > 0$ 且 $b < a \leq 3 b$ (3.3)

则方程(3.1)是以 $a, b, c$ 为长、短、对称半径的李氏卵圆方程。

(iii) 若

$a, b, c > 0$ 且 $a > 3 b$ (3.4)

则方程(3.1)是以 $a, b, c$ 为长、短、对称半径的李氏心脏线方程。

为了证明上述定理，我们先给出如下引理：

引理1：设(3.2)成立，(3.1)的图形为曲线L

(i) 若 $x_{0} \geq 0$ ，点 $(x_{0}, y_{0}) \in L$ ，则点 $(- x_{0}, y_{0}) \in L$ ；

(ii) 设l为平行于y轴的直线，若l与y轴的距离小于c，则L与l有且仅有两个交点；若l与y轴的距离等于c，则L与l有且仅有一个交点；若l与y轴的距离大于c，则L与l没有交点。

证明：(i) 由点 $(x_{0}, y_{0}) \in L$ ，则必存在 $t_{0} \in [- \frac{π}{2}, \frac{3 π}{2}]$ 满足(3.1)：

${\begin{cases} x_{0} = c \cos t_{0} \\ y_{0} = \frac{1}{2} [(a + b) - (a - b) \sin t_{0}] \sin t_{0} \end{cases}$

由 $x_{0} \geq 0$ 及 $c > 0$ 得 $\frac{x_{0}}{c} \geq 0$ ，故满足上式的第一式的

$t_{0} = \arccos \frac{x_{0}}{c} \in [0, \frac{π}{2}] \cup [- \frac{π}{2}, 0]$

若 $t_{0} \in [0, \frac{π}{2}]$ ，则取 ${\tilde{t}}_{0} = π - t_{0} \in [\frac{π}{2}, π]$ 。设 ${\tilde{t}}_{0}$ 对应于L上的点为 $({\tilde{x}}_{0}, {\tilde{y}}_{0})$ ，将 $t = {\tilde{t}}_{0}$ 代入(3.1)得点

$({\tilde{x}}_{0}, {\tilde{y}}_{0}) \in L$ ，则

${\tilde{x}}_{0} = c \cos {\tilde{t}}_{0} = c \cos (π - t_{0}) = - c \cos t_{0} = - x_{0}$

$\begin{matrix} {\tilde{y}}_{0} = \frac{1}{2} [(a + b) - (a - b) \sin {\tilde{t}}_{0}] \sin {\tilde{t}}_{0} \\ = \frac{1}{2} [(a + b) - (a - b) \sin (π - t_{0})] \sin (π - t_{0}) \\ = \frac{1}{2} [(a + b) - (a - b) \sin t_{0}] \sin t_{0} = y_{0} \end{matrix}$

故点 $(- x_{0}, y_{0}) = ({\tilde{x}}_{0}, {\tilde{y}}_{0}) \in L$ 。

若 $t_{0} \in [- \frac{π}{2}, 0]$ ，则取 ${\tilde{t}}_{0} = π - t_{0} \in [π, \frac{3 π}{2}]$ ，同理可证 $(- x_{0}, y_{0}) = ({\tilde{x}}_{0}, {\tilde{y}}_{0}) \in L$ 。

(ii) 设直线l到y轴的距离为k，则l的方程为

$x = k (0 \leq k < c)$ ，或 $x = - k (0 \leq k < c)$

将上式第一式代入L的方程，即(3.1)的第一式，得

$k = c \cos t$ 即 $\cos t = \frac{k}{c}$

当 $0 \leq k < c$ 时，有 $0 \leq \frac{k}{c} < 1$ ，故满足上式的t有且仅有两个解 $t_{1}$ ， $t_{2}$ 满足

$t_{1} = \arccos \frac{k}{c} \in (0, \frac{π}{2}], t_{2} = - t_{1} \in [- \frac{π}{2}, 0)$

设L上对应于 $t_{1}, t_{2}$ 的点分别为 $(x_{1}, y_{1}), (x_{2}, y_{2})$ ，则

$x_{2} = c c o s t_{2} = c c o s (- t_{1}) = c c o s t_{1} = x_{1} = k$

由(3.2)及 $t_{1} \in (0, \frac{π}{2}]$ 得

$y_{1} = \frac{1}{2} [(a + b) - (a - b) \sin t_{1}] \sin t_{1} > 0$

$y_{2} = \frac{1}{2} [(a + b) - (a - b) \sin (- t_{1})] \sin (- t_{1}) = - \frac{1}{2} [(a + b) + (a - b) \sin t_{1}] \sin t_{1} < 0$

故 $y_{1} \neq y_{2}$ ，从而 $(x_{1}, y_{1}) \neq (x_{2}, y_{2})$ ，即L与l有且仅有两个交点 $(k, y_{1}), (k, y_{2})$ 。

当 $k = c$ 时， $\cos t = 1$ ，显然t只有一个解 $t = 0$ ，故此时L与l只有一个交点 $(c, 0)$ 。

当 $k > c$ 时， $\cos t = \frac{k}{c}$ 无解，故此时L与l无交点。

对 $x = - k$ 的情形可同理证之。

引理2：设由参数式方程(3.1)所确定的y为x的函数的一阶和二阶导数分别记为 ${y^{'}}_{x} (t)$ 和 ${y^{″}}_{x} (t)$ ，则

${y^{'}}_{x} (t) = - \frac{1}{2 c} [(a + b) - 2 (a - b) \sin t] \cot t, t \in [- \frac{π}{2}, \frac{3 π}{2}]$ (3.5)

${y^{″}}_{x} (t) = - \frac{1}{2 c^{2} \sin^{3} t} [(a + b) - 2 (a - b) \sin^{3} t], t \in [- \frac{π}{2}, \frac{3 π}{2}]$ (3.6)

且(i) 若(3.2)成立，则

${y^{″}}_{x} (t) > 0, t \in (- \frac{π}{2}, 0) \cup (π, \frac{3 π}{2})$ (3.7)

(ii) 若(3.3)成立，则

${y^{″}}_{x} (t) \leq 0, t \in (0, π)$ (3.8)

(iii) 若(3.4)成立，则在 $(0, \frac{π}{2})$ 上必存在唯一的

$t_{0} = \arcsin \frac{a + b}{2 (a - b)} \in (0, \frac{π}{2})$ (3.9)

使

${y^{'}}_{x} (t_{0}) = 0$ (3.10)

且在 $(t_{0}, \frac{π}{2})$ 上存在唯一的

$t_{1} = \arcsin \sqrt[3]{\frac{a + b}{2 (a - b)}} \in (t_{0}, \frac{π}{2})$ (3.11)

使

${y^{″}}_{x} (t_{1}) = 0$ (3.12)

${y^{″}}_{x} (t) < 0, t \in (0, t_{1})$ (3.13)

${y^{″}}_{x} (t) > 0, t \in (t_{1}, \frac{π}{2})$ (3.14)

证明：由(3.1)得

${y^{'}}_{x} (t) = \frac{d y}{d x} = \frac{\frac{d y}{d t}}{\frac{d x}{d t}} = \frac{{\frac{1}{2} [(a + b) - (a - b) \sin t] \sin t}^{'}}{{(c \cos t)}^{'}}, t \in [- \frac{π}{2}, \frac{3 π}{2}]$

将上式化简即得(3.5)，又由(3.5)得

${y^{″}}_{x} (t) = \frac{d ({y^{'}}_{x} (t))}{d x} = \frac{{- \frac{1}{2 c} [(a + b) - 2 (a - b) \sin t] \cot t}^{'}}{{(c \cos t)}^{'}}, t \in [- \frac{π}{2}, \frac{3 π}{2}]$

将上式化简即得(3.6)。

(i) 因为当 $t \in (- \frac{π}{2}, 0) \cup (π, \frac{3 π}{2})$ 时，恒有 $\sin^{3} t < 0$ ，由此式及(3.2)和(3.6)即得(3.7)。

(ii) 因为当 $t \in (0, π)$ 时，恒有 $\sin^{3} t \leq 1$ ，由此式及(3.3)，知

$(a + b) - 2 (a - b) \sin^{3} t \geq (a + b) - 2 (a - b) = - a + 3 b \geq 0$ (3.15)

又显然有

$\sin^{3} t > 0, t \in (0, π)$ (3.16)

于是由(3.6)和(3.15)和(3.16)即得(3.8)。

(iii) 由(3.4)得

$0 < \frac{a + b}{2 (a - b)} < 1$ (3.17)

由正弦函数 $\sin t$ 在 $[0, \frac{π}{2}]$ 上严格单调递增及(3.17)知，存在唯一的 $t_{0} \in (0, \frac{π}{2})$ 使

$\sin t_{0} = \frac{a + b}{2 (a - b)}$ (3.18)

将(3.18)代入(3.5)，并注意到 $c > 0$ ，即得 ${y^{'}}_{x} (t_{0}) = 0$ ，即(3.9)和(3.10)成立。

又由(3.17)得

$0 < \frac{a + b}{2 (a - b)} < \sqrt[3]{\frac{a + b}{2 (a - b)}} < 1$ (3.19)

同样由正弦函数 $\sin t$ 在 $[0, \frac{π}{2}]$ 上严格单调递增及(3.19)知，存在唯一的 $t_{1} \in (t_{0}, \frac{π}{2})$ 使

$\sin t_{1} = \sqrt[3]{\frac{a + b}{2 (a + b)}}$ (3.20)

$\sin t < \sqrt[3]{\frac{a + b}{2 (a + b)}}, t \in (0, t_{1})$ (3.21)

$\sin t > \sqrt[3]{\frac{a + b}{2 (a + b)}}, t \in (t_{1}, \frac{π}{2})$ (3.22)

分别将(3.20)和(3.21)和(3.22)代入(3.6)，即得(3.12)和(3.13)和(3.14)。

定理1的证明：设(3.1)的曲线为L。

(i) 由(3.2)及引理1知，L关于y轴对称且是闭合的，故L满足定义1的条件①。

由(3.1)的第一式知， $t = 0$ 是函数 $x = c \cos t$ 在 $t \in [- \frac{π}{2}, \frac{3 π}{2}]$ 上唯一最大值点，且最大值为c，将 $t = 0$ 代

入式(3.1)的第二式得 $y = 0$ ，故L上存在唯一一对对称点 $S (c, 0)$ ， $T (- c, 0)$ ，它们到L的对称轴y轴的距离最大，故L满足定义1的条件②。

令 $x = 0$ ，则由(3.1)的第一式得 $t = \frac{π}{2}$ 或 $t = \frac{3}{2} π$ ，将它们代入(3.1)的第二式分别 $y = b$ 或 $y = - a$ ，故L

与其对称轴y轴有且仅有两个交点 $O (0, b)$ ， $O (0, - a)$ ，显然PQ与ST相交于坐标系原点 $O (0, 0)$ 且 $O P = a > b = O Q$ ，故L满足定义1的条件③。

由引理2之(3.5)知，导数 ${y^{'}}_{x} (t)$ 在 $t = 0$ 或 $t = π$ 时为 $\infty$ ，而在 $[- \frac{π}{2}, \frac{3 π}{2}]$ 的其它点均为有限存在，故曲

线L处处存在切线，从而处处光滑，所以L满足定义1的条件④。

因此曲线L是满足定义1的李氏卵形曲线，参数方程(3.1)为李氏卵形曲线方程。

(ii) 当(3.3)成立即 $0 < b < a \leq 3 b$ 时，必有(3.2)成立，从而由引理2之(i)即(3.7)知曲线L的下半部为下凸的，而由(3.3)及引理2之(ii)即(3.8)知曲线L的上半部为上凸的 [2]，故曲线L为凸的，又由(3.3)成立，则(3.2)必成立，从而由(i)知，L为李氏卵形曲线，又上面已证L处处光滑，所以曲线L为李氏卵圆。参数方程(3.1)为李氏卵圆方程。

(iii)当(3.4)成立即 $a > 3 b$ 时，由引理2之(iii)知(3.9)~(3.14)均成立，且(3.2)亦成立，从而(3.7)成立。

设曲线L上对应于 $t_{1}$ 的点为 $H_{1}$ ，则由(3.12)~(3.14)知点 $H_{1}$ 为曲线L的拐点 [2]；由对称性知， $t_{2} = π - t_{1}$ 所对应的点 $H_{2}$ 也是曲线L的拐点，且曲线L在 $t \in (0, t_{1})$ 上为上凸的，在 $t \in (t_{1}, t_{2})$ 上为下凸的，在 $t \in (t_{2}, π)$ 上为上凸的。所以曲线L的上半部仅在近端点处是向里凹的。

而当 $t \in (- \frac{π}{2}, 0) \cup (π, \frac{3 π}{2})$ 时，由(3.7)知，曲线L在 $t \in (- \frac{π}{2}, 0) \cup (π, \frac{3 π}{2})$ 上(即L的下半部)是下凸的。

这就证明了当(3.4)成立时，曲线L仅在近端点处向里凹；又由(3.4)成立，则(3.2)必成立，从而由(i)知，L为李氏卵形曲线。所以曲线L为李氏心脏线(参见图2)，参数方程(3.1)为李氏心脏线方程。

Figure 2. Li’s cardioids diagram

图2. 李氏心脏线示意图

注1：在(3.1)中令 $b = a, a > c$ ，则得 ${\begin{cases} x = c \cos t \\ y = a \sin t \end{cases}, t \in (- \frac{π}{2}, \frac{3 π}{2})$ ，此式正是长、短半轴为a，c的椭圆的

参数式方程。故李氏卵形曲线(3.1)是椭圆的推广。

4. 参数式李氏卵形曲线的周长和面积

定理2：设李氏卵形曲线(3.1)的长、短、对称半径分别为 $a, b, c$ ，曲线的周长为l，所围图形面积为S，则

$l = \frac{1}{2} \int_{- \frac{π}{2}}^{\frac{3 π}{2}} \sqrt{4 c^{2} \sin^{2} t + {[(a + b) - 2 (a - b) \sin t]}^{2} \cos^{2} t} d t$ (4.1)

$S = \frac{π}{2} (a + b) c$ (4.2)

证明：由文献 [2] 之P₂₇₇及文献 [3] 之P₁₄₅，知

$l = \int_{- \frac{π}{2}}^{\frac{3 π}{2}} \sqrt{{x^{'}}^{2} (t) + {y^{'}}^{2} (t)} d t$ (4.3)

$S = \frac{1}{2} \int_{- \frac{π}{2}}^{\frac{3 π}{2}} (x y^{'} - y x^{'}) d t$ (4.4)

将(3.1)及其导数代入(4.3)即得(4.1)。

将(3.1)及其导数代入(4.4)并化简，得

$\begin{array}{l} S = \frac{1}{2} \int_{- \frac{π}{2}}^{\frac{3 π}{2}} {\frac{1}{2} [(a + b) \cos t - (a - b) \sin 2 t] \cdot c \cos t + \frac{1}{2} [(a + b) - (a - b) \sin t] \sin t \cdot c \sin t} d t \\ = \frac{c}{4} \int_{- \frac{π}{2}}^{\frac{3 π}{2}} (a + b) (\sin^{2} t + \cos^{2} t) d t - \frac{c}{4} \int_{- \frac{π}{2}}^{\frac{3 π}{2}} (a - b) \sin 2 t \cos t d t - \frac{c}{4} \int_{- \frac{π}{2}}^{\frac{3 π}{2}} (a - b) \sin^{3} t d t \end{array}$

而

$\frac{c}{4} \int_{- \frac{π}{2}}^{\frac{3 π}{2}} (a + b) (\sin^{2} t + \cos^{2} t) d t = \frac{c}{4} \int_{- \frac{π}{2}}^{\frac{3 π}{2}} (a + b) d t = \frac{π}{2} (a + b) c$

$\frac{c}{4} \int_{- \frac{π}{2}}^{\frac{3 π}{2}} (a - b) \sin 2 t \cos t d t = \frac{(a - b) c}{2} \int_{- \frac{π}{2}}^{\frac{3 π}{2}} \cos^{2} t \sin t d t = - \frac{(a - b) c}{2} \int_{- \frac{π}{2}}^{\frac{3 π}{2}} \cos^{2} t d \cos t = - \frac{(a - b) c}{2} \int_{0}^{0} u^{2} d u = 0$

$\frac{c}{4} \int_{- \frac{π}{2}}^{\frac{3 π}{2}} (a - b) \sin^{3} t d t = - \frac{(a - b) c}{4} \int_{- \frac{π}{2}}^{\frac{3 π}{2}} (1 - \cos^{2} t) d \cos t = - \frac{(a - b) c}{4} \int_{0}^{0} (1 - u^{2}) d u = 0$

故 $S = \frac{π}{2} (a + b) c$ ，即(4.2)成立。

注2：在(4.2)中令 $b = a, a > c$ ，则得 $S = π a c$ ，此式正是长、短半轴为 $a, c$ 的椭圆的面积公式，这也佐证了(4.2)的正确性。

5. 参数式李氏卵形曲线所围图形的质心

定理3：设李氏卵形曲线(3.1)的长、短、对称半径分别为 $a, b, c$ ，曲线所围图形的质心为 $(\bar{x}, \bar{y})$ ，则

${\begin{cases} \bar{x} = 0 \\ \bar{y} = - \frac{3}{8} (a - b) \end{cases}$ (5.1)

证明：由对称性显然有 $\bar{x} = 0$

设参数式(3.1)的卵形曲线的上半部为 $y_{2} (x)$ ，下半部为 $y_{1} (x)$ ，则由(3.1)可得

$y_{2} (x) = \frac{1}{2 c^{2}} [c (a + b) \sqrt{c^{2} - x^{2}} - (a - b) (c^{2} - x^{2})], x \in [- c, c]$ (5.2)

$y_{1} (x) = - \frac{1}{2 c^{2}} [c (a + b) \sqrt{c^{2} - x^{2}} - (a - b) (c^{2} - x^{2})], x \in [- c, c]$ (5.3)

又设卵形曲线(3.1)所围图形对x轴的静力矩为 $M_{x}$ ，则由文献 [4] 之P₂₂₉知

$M_{x} = \frac{1}{2} \int_{- c}^{c} (y_{2}^{2} - y_{1}^{2}) d x$ (5.4)

将(5.2)和(5.3)代入(5.4)并化简，得

$M_{x} = - \frac{a^{2} - b^{2}}{2 c^{3}} \int_{- c}^{c} (c^{2} - x^{2}) \sqrt{c^{2} - x^{2}} d x$

上式中令 $x = c \sin t$ ，换元积分之，得

$\begin{array}{l} M_{x} = - \frac{a^{2} - b^{2}}{2 c^{3}} \int_{- \frac{π}{2}}^{\frac{π}{2}} c^{4} \cos^{4} t d t = - \frac{(a^{2} - b^{2}) c}{2} \int_{- \frac{π}{2}}^{\frac{π}{2}} \frac{1}{8} (3 + 4 \cos 2 t + \cos 4 t) d t \\ = - \frac{(a^{2} - b^{2}) c}{16} \int_{- \frac{π}{2}}^{\frac{π}{2}} 3 d t = - \frac{3 (a^{2} - b^{2}) c π}{16} \end{array}$ (5.5)

又由文献 [4] 之P₂₂₆知

$\bar{y} = \frac{M_{x}}{S}$ (5.6)

将(5.5)和(4.2)代入(5.6)即得 $\bar{y} = - \frac{3}{8} (a - b)$ ，故(5.1)成立。

6. 参数式李氏卵形曲线所围图形的转动惯量

定理4：设李氏卵形曲线(3.1)的长、短、对称半径分别为 $a, b, c$ ，曲线所围图形绕y轴的转动惯量为 $I_{y}$ ，则

$I_{y} = \frac{1}{4} M c^{2}$ (6.1)

其中

$M = \frac{1}{2} π (a + b) c ρ$ (6.2)

是面密度为常数 $ρ$ 的卵形曲线薄片的质量。

证明：由文献 [4] 之P₂₃₉知

$I_{y} = \int_{- c}^{c} ρ x^{2} (y_{2} - y_{1}) d x$

将(5.2)和(5.3)代入上式，并化简，得

$\begin{array}{l} I_{y} = \frac{(a + b) ρ}{c} \int_{- c}^{c} x^{2} \sqrt{c^{2} - x^{2}} d x = \frac{2 (a + b) ρ}{c} \int_{0}^{c} x^{2} \sqrt{c^{2} - x^{2}} d x \\ = \frac{2 (a + b) ρ}{c} \int_{0}^{\frac{π}{2}} c^{2} \sin^{2} t \cdot c \cos t d (c \sin t) = 2 (a + b) c^{3} ρ \int_{0}^{\frac{π}{2}} {(\sin t \cos t)}^{2} d t \\ = \frac{(a + b) c^{3} ρ}{2} \int_{0}^{\frac{π}{2}} {(\sin 2 t)}^{2} d t = \frac{(a + b) c^{3} ρ}{2} \int_{0}^{\frac{π}{2}} \frac{1 - \cos 4 t}{2} d t \\ = \frac{(a + b) c^{3} ρ}{4} {[t - \frac{1}{4} \sin 4 t]}_{0}^{\frac{π}{2}} = \frac{π}{8} (a + b) ρ c^{3} = \frac{1}{4} M c^{2} \end{array}$

其中 $M = \frac{1}{2} π (a + b) c ρ$ 。故(6.1)，(6.2)成立。

7. 参数式李氏卵形曲线的曲率和曲率半径

定理5：设李氏卵形曲线(3.1)的长、短、对称半径分别为 $a, b, c$ ，曲线曲率为K，曲率半径为R，则

$K = \frac{4 c | (a + b) - 2 (a - b) \sin^{3} t |}{{4 c^{2} \sin^{2} t + {[(a + b) \cos t - (a - b) \sin 2 t]}^{2}}^{3 / 2}}$ (7.1)

$R = \frac{{4 c^{2} \sin^{2} t + {[(a + b) \cos t - (a - b) \sin 2 t]}^{2}}^{3 / 2}}{4 c | (a + b) - 2 (a - b) \sin^{3} t |}$ (7.2)

证明：由文献 [2] 之P₁₇₁知参数式表示的曲线的曲率K和曲率半径R，有公式

$K = \frac{| \dot{x} \ddot{y} - \ddot{x} \dot{y} |}{{({\dot{x}}^{2} + {\dot{y}}^{2})}^{3 / 2}}$ (7.3)

$R = \frac{{({\dot{x}}^{2} + {\dot{y}}^{2})}^{3 / 2}}{| \dot{x} \ddot{y} - \ddot{x} \dot{y} |}$ (7.4)

由式(3.1)得

$\dot{x} = - c \sin t$

$\ddot{x} = - c \cos t$

$\dot{y} = - \frac{1}{2} [(a + b) \cos t - (a - b) \sin 2 t]$

$\ddot{y} = - \frac{1}{2} [(a + b) \sin t + 2 (a - b) \cos 2 t]$

将上诸式分别代入式(7.3)与(7.4)，并化简，即得式(7.1)和(7.2)。

特别：由式(7.2)即知，对应于 $t = - \frac{π}{2}, 0, \frac{π}{2}, π$ 的点处的曲率半径分别为

$R (- \frac{π}{2}) = \frac{2 c^{2}}{3 a - b}$ (7.5)

$R (0) = \frac{{(a + b)}^{2}}{4 c}$ (7.6)

$R (\frac{π}{2}) = \frac{2 c^{2}}{| - a + 3 b |}$ (7.7)

$R (π) = \frac{{(a + b)}^{2}}{4 c}$ (7.8)

8. 参数式李氏卵形曲线旋转卵形体的体积

定理6：设李氏卵形曲线(3.1)的长、短、对称半径分别为 $a, b, c$ ，曲线所围图形绕y轴旋转而成的旋转卵形体的体积为V，则

$V = \frac{2}{3} π (a + b) c^{2}$ (8.1)

证明：由文献 [2] 之P₂₇₃及(3.1)知，旋转卵形体的体积

$\begin{array}{l} V = π \int_{- a}^{b} x^{2} d y = π \int_{- \frac{π}{2}}^{\frac{π}{2}} x^{2} (t) y^{'} (t) d t = π \int_{- \frac{π}{2}}^{\frac{π}{2}} c^{2} \cos^{2} t \cdot \frac{1}{2} [(a + b) \cos t - 2 (a - b) \cos t \sin t] d t \\ = \frac{π (a + b) c^{2}}{2} \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{3} t d t - π (a - b) c^{2} \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{3} t \sin t d t \\ = \frac{π (a + b) c^{2}}{2} \int_{- \frac{π}{2}}^{\frac{π}{2}} \frac{3 \cos t + \cos 3 t}{4} d t + π (a - b) c^{2} \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{3} t d \cos t \\ = \frac{π (a + b) c^{2}}{2} {[\frac{3}{4} \sin t + \frac{1}{12} \sin 3 t]}_{- \frac{π}{2}}^{\frac{π}{2}} + π (a - b) c^{2} \int_{0}^{0} u^{3} d u = \frac{π (a + b) c^{2}}{2} \cdot \frac{4}{3} + 0 = \frac{2}{3} π (a + b) c^{2} \end{array}$

故(8.1)成立。

注3：在(8.1)中，令 $b = a$ ， $a > c$ ，则得 $V = \frac{4}{3} π a c^{2}$ ，此式正是长、短半轴分别为 $a, c$ 的旋转椭球的

体积公式。这也佐证了(8.1)的正确性。

9. 参数式李氏卵形曲线的几何作法

由(3.1)可得参数式李氏卵形曲线的几何作法，其作图步骤如下：

首先约定以O为圆心，r为半径的圆表示为圆 $(O; r)$ ；

1) 以直角坐标系的原点O为圆心，c为半径作图 $(O; c)$ 交x轴于点A，以O为圆心， $a - b$ 为半径作圆 $(O; a - b)$ ；

2) 以O为顶点，OA为始边作 $∠ A O B = t, t \in [- \frac{π}{2}, \frac{3 π}{2}]$ ，OB交圆 $(O; c)$ 于点D，OB的反向延长线交

圆 $(O; a - b)$ 于点E；

3) 从点E作x轴的垂线，垂足为F；

4) 在射线OB上取 $O G = \frac{1}{2} (a + b \pm E F)$ ， $t \in [0, π]$ 时取“−”， $t \in [- \frac{π}{2}, 0] \cup [π, \frac{3 π}{2}]$ 时取“+”；

5) 过点D作x轴的垂线，过点G作y轴的垂线，两垂线交于点 $M_{t}$ ，则点 $M_{t}$ 就是参数式李氏卵形曲线(3.1)上对应于参数t的点。如此作出若干个这样的 $M_{t}$ 点，连起来就可获得方程(3.1)的图形，如图3所示。

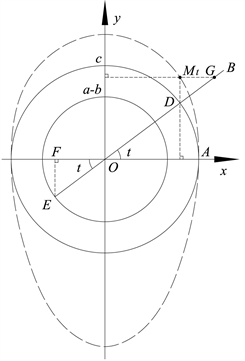
Figure 3. Geometric drawing of Li’s oval curve (3.1)

图3. 李氏卵形曲线(3.1)的几何作法示意图

10. 参数式李氏卵形曲线旋转卵形体的质心

定理7：设李氏卵形曲线(3.1)的长、短、对称半径分别为 $a, b, c$ ，曲线绕y轴旋转而成的旋转卵形体的质心为 $(\bar{x}, \bar{y}, \bar{z})$ ，则

${\begin{cases} \bar{x} = 0 \\ \bar{y} = - \frac{3}{10} (a - b) \\ \bar{z} = 0 \end{cases}$ (10.1)

证明：由文献 [4] 之P₂₃₆知

$\bar{y} = \frac{π \int_{- a}^{b} y x^{2} d y}{V}$ (10.2)

又

$\begin{array}{l} \int_{- a}^{b} y x^{2} d y = \int_{- \frac{π}{2}}^{\frac{π}{2}} y (t) x^{2} (t) y^{'} (t) d t \\ = \int_{- \frac{π}{2}}^{\frac{π}{2}} c \cos t \frac{1}{2} [(a + b) - (a - b) \sin t] \sin t \frac{1}{2} [(a + b) \cos t - (a - b) \sin 2 t] d t \\ = \frac{1}{4} c^{2} {(a + b)}^{2} \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{3} t \sin t d t - \frac{3}{4} c^{2} (a^{2} - b^{2}) \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{3} t \sin^{2} t d t - \frac{1}{2} c^{2} {(a - b)}^{2} \int_{- \frac{π}{2}}^{\frac{π}{2}} \sin^{3} t \cos^{3} t d t \end{array}$ (10.3)

而

$\int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{3} t \sin t d t = \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{3} t d \cos t = \int_{0}^{0} u^{3} d u = 0$ (10.4)

$\int_{- \frac{π}{2}}^{\frac{π}{2}} \sin^{3} t \cos^{3} t d t = \frac{1}{8} \int_{- \frac{π}{2}}^{\frac{π}{2}} \sin^{3} 2 t d t = \frac{1}{32} \int_{- \frac{π}{2}}^{\frac{π}{2}} (3 \sin 2 t - \sin 6 t) d t = \frac{1}{32} {[- \frac{3}{2} \cos 2 t + \frac{1}{6} \cos 6 t]}_{- \frac{π}{2}}^{\frac{π}{2}} = 0$ (10.5)

$\begin{array}{l} \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{3} t c \sin^{2} t d t = \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{2} t c \sin^{2} t d \sin t = \int_{- \frac{π}{2}}^{\frac{π}{2}} (1 - \sin^{2} t) \sin^{2} t d \sin t \\ = \int_{- 1}^{1} (1 - u^{2}) u^{2} d u = {[\frac{u^{3}}{3} - \frac{u^{5}}{5}]}_{- 1}^{1} = \frac{4}{15} \end{array}$ (10.6)

将(10.4)和(10.5)和(10.6)代入(10.3)得

$\int_{- a}^{b} y x^{2} d y = - \frac{3}{4} c^{2} (a^{2} - b^{2}) \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos^{3} t \sin^{2} t d t = - \frac{3}{4} c^{2} (a^{2} - b^{2}) \cdot \frac{4}{15} = - \frac{3}{15} c^{2} (a^{2} - b^{2})$ (10.7)

由(10.2)和(10.7)和(8.1)得

$\bar{y} = \frac{- \frac{3}{15} π c^{2} (a^{2} - b^{2})}{\frac{2}{3} π (a + b) c^{2}} = - \frac{3}{10} (a - b)$ (10.8)

由对称性知 $\bar{x} = 0$ ， $\bar{z} = 0$ ，故(10.1)成立。

11. 参数式(3.1)为关于x，y的四次方程

由参数式(3.1)的第二个式子得

$(a - b) \sin^{2} t - (a + b) \sin t + 2 y = 0$

则

$\sin t = \frac{(a + b) \pm \sqrt{{(a + b)}^{2} - 8 (a - b) y}}{2 (a - b)}$

$\sin^{2} t = {[\frac{(a + b) \pm \sqrt{{(a + b)}^{2} - 8 (a - b) y}}{2 (a - b)}]}^{2}$

又由(3.1)的第一个式子得

$\cos^{2} t = \frac{x^{2}}{c^{2}}$

将上两式相加，并注意到 $\sin^{2} t + \cos^{2} t = 1$ ，则得

$\frac{x^{2}}{c^{2}} + \frac{{[(a + b) \pm \sqrt{{(a + b)}^{2} - 8 (a - b) y}]}^{2}}{4 {(a - b)}^{2}} = 1$

上式化简即得

${(a - b)}^{2} x^{4} - 4 c^{2} (a - b) x^{2} y - c^{2} (a^{2} - 6 a b + b^{2}) x^{2} + 4 c^{4} y^{2} + 4 c^{4} (a - b) y - 4 a b c^{4} = 0$ (11.1)

故式(11.1)是和参数式(3.1)等价的。从而由定理1可得如下

定理8：(i) 若(3.2)成立，则(11.1)是以 $a, b, c$ 为长、短、对称半径的李氏卵形曲线方程;

(ii) 若(3.3)成立，则(11.1)是以 $a, b, c$ 为长、短、对称半径的李氏卵圆方程;

(iii) 若(3.4)成立，则(11.1)是以 $a, b, c$ 为长、短、对称半径的李氏心脏线方程。

定理9：设四次方程

$A x^{4} - 2 \sqrt{A D} x^{2} y + \frac{4 F - A D}{2 \sqrt{D}} x^{2} + D y^{2} + D \sqrt{A} y - F = 0$ (11.2)

(i) 若

$A, D, F > 0$ (11.3)

则(11.2)是李氏卵形曲线方程，且其长、短、对称半径

${\begin{cases} a = \frac{D \sqrt{A} + \sqrt{A D + 4 D F}}{2 D} \\ b = \frac{- D \sqrt{A} + \sqrt{A D + 4 D F}}{2 D} \\ c = \sqrt[4]{\frac{D}{4}} \end{cases}$ (11.4)

(ii) 若

$A, D, F > 0$ 且 $A \leq \frac{4 F}{3 D}$ (11.5)

则(11.2)是李氏卵圆方程，且其长、短、对称半径如(11.4)所示。

(iii) 若

$A, D, F > 0$ 且 $A > \frac{4 F}{3 D}$ (11.6)

则(11.2)是李氏心脏线方程，且其长、短、对称半径如(11.4)所示。

证明：考察如下的四次方程

$A x^{4} - B x^{2} y + C x^{2} + D y^{2} + E y - F = 0$ (11.7)

比较(11.7)与(11.1)的系数，得

$A = {(a - b)}^{2}$ (11.8)

$B = 4 c^{2} (a - b)$ (11.9)

$C = c^{2} [4 a b - {(a - b)}^{2}]$ (11.10)

$D = 4 c^{4}$ (11.11)

$E = 4 c^{4} (a - b)$ (11.12)

$F = 4 a b c^{4}$ (11.13)

由(11.8)得

$a - b = \sqrt{A}$ (11.14)

由(11.11)及(11.13)得

$a b = \frac{F}{D}$ (11.15)

由(11.9)，(11.11)，(11.14)得

$B = 2 \sqrt{A D}$ (11.16)

由(11.10)，(11.11)，(11.15)，(11.8)得

$C = \sqrt{\frac{D}{4}} (4 \frac{F}{D} - A) = \frac{4 F - A D}{2 \sqrt{D}}$ (11.17)

由(11.12)，(11.11)，(11.8)得

$E = D \sqrt{A}$ (11.18)

将(11.16)，(11.17)，(11.18)代入(11.7)，即得(11.2)。又由(11.8)，(11.11)，(11.13)可得

${\begin{cases} A = {(a - b)}^{2} \\ D = 4 c^{4} \\ F = 4 a b c^{4} \end{cases}$ (11.19)

由(11.19)反解即得(11.4)。

(i) 由(11.4)及(11.9)得

$a, b, c > 0$ 且 $a > b \Leftrightarrow A, D, F > 0$

故由定理8之(i)即知本定理之(i)成立。

(ii) 将(11.4)的前两式代入(3.3)，得

$\begin{array}{l} a \leq 3 b \Leftrightarrow \sqrt{A} D + \sqrt{A D^{2} + 4 D F} \leq 3 (- \sqrt{A} D + \sqrt{A D^{2} + 4 D F}) \\ \Leftrightarrow 4 \sqrt{A} D \leq 2 \sqrt{A D^{2} + 4 D F} \\ \Leftrightarrow 3 A D^{2} \leq 4 D F \\ \Leftrightarrow A \leq \frac{4 F}{3 D} \end{array}$

由上式及定理8之(ii)即得本定理之(ii)。

(iii) 将(11.4)的前两式代入(3.4)，并仿(ii)之推导，得

$a \leq 3 b \Leftrightarrow \dots \Leftrightarrow A > \frac{4 F}{3 D}$

由上式及定理8之(iii)即得本定理之(iii)。

12. 示例与仿真验证

12.1. 示例

只要给出李氏卵形曲线的长、短、对称半径 $a, b, c$ 三个特征参数的具体数值，代入(3.1)或(11.1)就可得到具体的李氏卵形曲线方程。

例1：设 $a = 8$ ， $b = 6$ ， $c = 5$ ，代入(3.1)或(11.1)得

${\begin{cases} x = 5 \cos t \\ y = 7 \sin t - \sin^{2} t \end{cases}, t \in [- \frac{π}{2}, \frac{3 π}{2}]$ (12.1)

$4 x^{4} - 200 x^{2} y + 4700 x^{2} + 2500 y^{2} + 5000 y - 120000 = 0$ (12.2)

即

$x^{4} - 50 x^{2} y + 1175 x^{2} + 625 y^{2} + 1250 y - 30000 = 0$ (12.3)

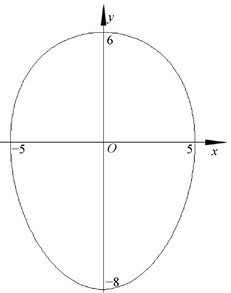
注意到这时有 $a, b, c > 0$ 且 $b < a \leq 3 b$ ，故由定理1之(ii)和定理8之(ii)知，(12.1)或(12.2)或(12.3)为李氏卵圆方程。曲线图形如图4所示。

Figure 4. Equation (12.1) graphics

图4. 方程(12.1)的图形

例2：设 $a = 8$ ， $b = 0.4$ ， $c = 5$ ，代入(3.1)或(11.1)得

${\begin{cases} x = 5 \cos t \\ y = 4.2 \sin t - 3.8 \sin^{2} t \end{cases}, t \in [- \frac{π}{2}, \frac{3 π}{2}]$ (12.4)

$57.76 x^{4} - 760 x^{2} y + 1124 x^{2} + 2500 y^{2} + 19000 y - 8000 = 0$ (12.5)

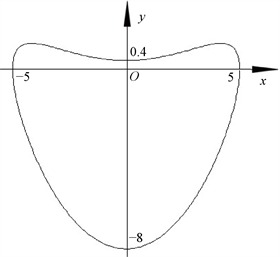
注意到这时有 $a, b, c > 0$ 且 $a > 3 b$ ，故由定理1之(iii)和定理8之(iii)知，(12.4)及(12.5)为李氏心脏线方程。曲线图形如图5所示。

12.2. 仿真验证

为了验证本文所建参数式李氏卵圆方程图形与真实卵形对比效果，用计算机编写了一个仿真绘图程序。取一张鸡蛋照片作为绘图程序界面上绘图区的背景。通过像素分析和计算，获得图片中鸡蛋图像长方向最大像素为386，宽方向最大像素为294，在鸡蛋图片横向和纵向最大像素处画两条直线作为x轴和y轴，x轴与y轴的交点即为鸡蛋的卵心，并将卵心位置设定为绘图区的原点。程序界面如图6(a)所示。

Figure 5. Equation (12.4) graphics

图5. 方程(12.4)的图形

(a) 绘图程序界面 (b) 绘图程序运行结果

Figure 6. Drawing program of simulating

图6. 仿真绘图程序

按参数式李氏卵形曲线方程的需求量取鸡蛋以像素为单位的长、短、对称半径三个参数值，得出 $a = 206$ ， $b = 180$ ， $c = 147$ ，且满足 $b < a \leq 3 b$ ，则由(3.1)即得其卵圆方程：

${\begin{cases} x = 147 \cos t \\ y = (193 - 13 \sin t) \sin t \end{cases}, t \in [- \frac{π}{2}, \frac{3 π}{2}]$ (12.6)

绘图程序使用方程式(12.6)进行计算并通过描点法绘制图形，界面右侧文本框中显示方程取点的计算值。程序运行结果见图6(b)。

图6(b)中鸡蛋外轮廓的黑色绘图线是绘图程序根据方程式(12.6)绘制的卵圆图形，图线准确地通过鸡蛋的近端点、远端点和两个对称端点四个端点，与图片中鸡蛋外轮廓高度吻合。

13. 结语

鉴于到目前为止，人们对卵形曲线和卵圆还没有一个明确统一的定义，本文对卵形曲线和卵圆给出了一种精确定义，且为了叙述方便将这种新定义的卵形曲线和卵圆取名为李氏卵形曲线和李氏卵圆，同时提出了一类非常实用的参数式李氏卵形曲线方程，并推导出其周长、面积、质心坐标、转动惯量和旋转卵形体的体积等重要公式，为卵形曲线及其应用研究提供理论基础，也给卵形曲线的工程应用带来极大的方便。

文章引用

李湘江. 一类参数式李氏卵形曲线
A Kind of Parametric Li’s Oval Curve[J]. 应用数学进展, 2021, 10(01): 311-327. https://doi.org/10.12677/AAM.2021.101036

参考文献

1. 李湘江. 一类四次李氏卵圆[J]. 应用数学进展, 2019, 8(2): 193-202.

2. 同济大学应用数学系. 高等数学第五版上册[M]. 北京: 高等教育出版社, 2002: 148-149, 171, 273, 277.

3. 同济大学应用数学系. 高等数学第五版下册[M]. 北京: 高等教育出版社, 2002: 145.

4. Г. М. 菲赫金哥尔茨, 著. 北京大学高等数学教研组, 译. 微积分学教程二册一分册[M]. 北京: 人民教育出版社, 1959: 226, 236, 239.

期刊菜单