给定度序列具有最小覆盖成本的树 The Minimum Cover Cost of a Tree with Given Degree Sequence

doi:10.12677/AAM.2021.107270

Advances in Applied Mathematics
Vol. 10 No. 07 ( 2021 ), Article ID: 44219 , 9 pages
10.12677/AAM.2021.107270

给定度序列具有最小覆盖成本的树

贾雁宇，李玉瑛^*，郝艺方

●How to Cite this Article

太原理工大学数学学院，山西晋中

收稿日期：2021年6月26日；录用日期：2021年7月19日；发布日期：2021年7月28日

摘要

图G上顶点v的覆盖成本定义为 $C C_{G} (v) = \sum_{u \in V (G)} H_{v u}$ ， $H_{v u}$ 是从v开始随机游走到达u的平均首达时间。本文研究了给定度序列树的覆盖成本，并且刻画出覆盖成本最小的树。

关键词

度序列，覆盖成本，贪婪树

The Minimum Cover Cost of a Tree with Given Degree Sequence

Yanyu Jia, Yuying Li^*, Yifang Hao

School of Mathematics, Taiyuan University of Technology, Jinzhong Shanxi

Received: Jun. 26^th, 2021; accepted: Jul. 19^th, 2021; published: Jul. 28^th, 2021

ABSTRACT

The cover cost of a vertex v in G is defined as $C C_{G} (v) = \sum_{u \in V (G)} H_{v u}$ , where $H_{v u}$ is the expected hitting time for random walk beginning at v to visit u. In this paper, we study the cover cost of trees and characterize the unique tree with the minimum cover cost with given degree sequence.

Keywords:Degree Sequence, Cover Cost, Greedy Tree

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

设G为具有顶点集 $V (G) = {v_{1}, v_{2}, \dots, v_{n}}$ 和边集 $E (G)$ 的简单连通图。任给 $v \in V (G)$ ，v的度是与v关联的边的数目，用 $d (v)$ 表示。令 $d (v_{i}) = d_{i}, i = 1, 2, \dots, n$ ，则非增序列 $π = (d_{1}, d_{2}, \dots, d_{n})$ 称为G的度序

列。图G中度至少为3的顶点称为分支点，度为1的顶点称为叶子点或者悬挂点。

Wiener指数是指图G的所有顶点对的距离和，即 $W (G) = \sum_{{u, v} \subseteq V (G)} d_{G} (u, v) = \frac{1}{2} \sum_{v \in V (G)} D_{G} (v)$ ，这里 $D_{G} (v) = \sum_{u \in V (G)} d_{G} (v, u)$ 。直到现在，Wiener指数在各种图族中被广泛研究，一些结论可以在 [1] [2] [3]

中找到。

我们称树 $(T, r)$ 是以顶点r为根的树，在这个有根树中， $P_{T} (v, u)$ 表示树T中连通顶点 $v, u$ 的唯一路， $d_{T} (v, u)$ 为路 $P_{T} (v, u)$ 上边的数目，顶点v的高度定义为 $h_{T} (v) = d_{T} (r, v)$ 。在 $(T, r)$ 中，对于任意两个不同的顶点 $u, v$ ，如果 $P_{T} (r, u) \subset P_{T} (r, v)$ ，称v是u的后序点，u是v的前序点。如果v和u相邻且 $d_{T} (r, u) = d_{T} (r, v) - 1$ ，称u是v的parent，v是u的child。如果两个顶点 $u, v$ 有同一个parent，则称 $u, v$ 是

siblings。

2008年，Wang Hua [2] 刻画出给定度序列使Wiener指数最小化的树是贪婪树。2012年，Georgakopoulos

[4] 在图G中定义了顶点v的覆盖成本 $C C_{G} (v)$ 是从v开始随机游走到达图中所有顶点的平均首达时间总和，即 $C C_{G} (v) = \sum_{u \in V (G)} H_{v u}$ ，并研究了覆盖成本的性质。2015年，Georgakopoulos和Wagner [5] 在图G中定义了顶点v的反向覆盖成本 $R C_{G} (v) = \sum_{u \in V (G)} H_{u v}$ ，并且得到了树的覆盖成本与Wiener指数关系的公式以及反向覆盖成本与Wiener指数关系的公式，即对于树T和任给 $v \in V (T)$ ，有

$C C_{T} (v) = 2 W (T) - D_{T} (v)$ ，

$R C_{T} (v) = (2 n - 1) D_{T} (v) - 2 W (T)$ 。

他们确定了给定阶数树的覆盖成本，反向覆盖成本和首达时间的极值和极图。2019年，李书超和王书晶 [6] 在给定片段序列的情况下，刻画出覆盖成本最小及反向覆盖成本最小的树，也找到了反向覆盖成本最大的唯一树。2021年，张慧慧和李书超 [7] 在给定直径，匹配数和控制数的情况下，得出覆盖成本和反向覆盖成本的上下界，并刻画了对应的极图。

基于以上研究，本文在给定度序列的情况下，刻画出覆盖成本最小的树。

2. 预备知识

下面介绍本文用到的一些定义和定理。

定理2.1 [5]. 对于树T和任给 $v \in V (T)$ ，有

$C C_{T} (v) = 2 W (T) - D_{T} (v)$ ,

$R C_{T} (v) = (2 n - 1) D_{T} (v) - 2 W (T)$ .

定义集合 $L (T) = {v \in V (T) | D_{T} (v) \geq D_{T} (u), \forall u \in V (T)}$ 。

定理2.2 [6]. 任给树T， $v \in V (T)$ 当且仅当 $C C_{T} (v) = \min_{u \in V (T)} C C_{T} (u)$ 当且仅当 $R C_{T} (v) = \max_{u \in V (T)} R C_{T} (u)$ 。任给 $v \in V (T)$ ，v是悬挂点。

定义2.1 [2]. 给定非叶子点的度，贪婪树通过下面的贪婪算法得到：

1) 将最大度的顶点命名为v (根)；

2) 将与v相邻的顶点依次命名为 $v_{1}, v_{2}, \dots$ ，给这些顶点分配可用的最大度且满足 $d (v_{1}) \geq d (v_{2}) \geq \dots$ ；

3) 将与 $v_{1}$ 相邻的顶点依次命名为 $v_{11}, v_{12}, \dots$ (v除外)，给这些点分配可用的最大度且满足 $d (v_{11}) \geq d (v_{12}) \geq \dots$ ，顶点 $v_{2}, v_{3}, \dots$ 做法类似。

4) 对所有新命名的顶点重复3)，总是从已命名且度最大的顶点的未命名邻集开始。

从上面的定义中可以得出贪婪树的性质如下：

定理2.3 [2]. 给定度序列的有根树T是贪婪树，如果满足下面条件：

1) 根v具有最大度；

2) 任意两个叶子点的高度差至多是1；

3) 对于任意两个顶点u和w，如果 $h_{T} (w) < h_{T} (u)$ ，则 $d (w) \geq d (u)$ ；

4) 对于有相同高度的任意两个顶点 $u, w$ ，如果 $d (u) > d (w)$ ，则 $d (u^{'}) \geq d (w^{'})$ ， $u^{'}, w^{'}$ 分别是 $u, w$ 的后序点， $u^{'}$ 和 $w^{'}$ 高度相同；

5) 对于有相同高度的任意两个顶点 $u, w$ ，如果 $d (u) > d (w)$ ，则 $d (u^{'}) \geq d (w^{'})$ ， $d (u^{″}) \geq d (w^{″})$ ， $u^{'}, w^{'}$ 分别是 $u, w$ 的siblings， $u^{″}, w^{″}$ 分别是 $u^{'}, w^{'}$ 的后序点， $u^{'}$ 和 $w^{'}$ 高度相同， $u^{″}$ 和 $w^{″}$ 高度相同。

例1．度序列为 $(4, 4, 4, 3, 3, 3, 3, 3, 3, 3, 2, 2, 1, \dots, 1)$ (1的重数为15)的贪婪树如图1所示。

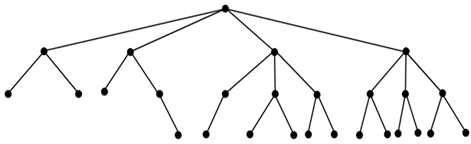
Figure 1. Greedy tree with degree sequence of (4,4,4,3,3,3,3,3,3,3,2,2,1,…,1)

图1. 度序列为(4,4,4,3,3,3,3,3,3,3,2,2,1,…,1)的贪婪树

3. 主要结论

本节研究给定度序列树的覆盖成本，并且称该条件下覆盖成本最小的树是理想树。

在理想树中选一条路，移除这条路上的所有边之后，如果一些连通分支仍然存在，取一个点将其命

名为z，将点z右边的顶点依次命名为 $x_{1}, x_{2}, \dots$ ，将点z左边的顶点依次命名为 $y_{1}, y_{2}, \dots$ 。令 $X_{i}, Y_{i}, Z (i = 1, 2, \dots)$ 表示包含对应顶点的分支， $X_{> k}$ 和 $Y_{> k}$ 分别表示由 $V (X_{k + 1}) \cup V (X_{k + 2}) \cup \dots$ 和 $V (Y_{k + 1}) \cup V (Y_{k + 2}) \cup \dots$ 导出的子树，如图2。不失一般性，假设 $| V (X_{1}) | \geq | V (Y_{1}) |$ 。

Figure 2. The components resulted from a path with z

图2. 带有顶点z的路产生的分支

定理3.1. 在如上描述的情形中，对于 $i = 1, 2, \dots, k$ ，如果有 $| V (X_{i}) | \geq | V (Y_{i}) |$ ，则在理想树中满足 $| V (X_{> k}) | \geq | V (Y_{> k}) |$ 。

证明：假设在理想树中 $| V (X_{> k}) | \geq | V (Y_{> k}) |$ 不成立，下面证明交换 $X_{> k}$ 和 $Y_{> k}$ 的位置不增加覆盖成本。当路的末端顶点都在或都不在 $V (Y_{> k}) \cup V (X_{> k})$ 中，交换 $X_{> k}$ 和 $Y_{> k}$ 的位置，这两点之间的距离不会改变。因此考虑只有一个末端顶点在 $V (Y_{> k}) \cup V (X_{> k})$ 的情况。

先计算 $W (T^{'}) - W (T)$ ，分为下面四种情况：

1) 对于 $V (X_{i}) (i = 1, 2, \dots, k)$ 中的任一顶点和 $X_{> k}$ 中的任一顶点，交换 $X_{> k}$ 和 $Y_{> k}$ 的位置，两点之间的距离增加2i，则总的Wiener指数增加 $\sum_{i = 1}^{k} (2 i) | V (X_{i}) | | V (X_{> k}) |$ ；

2) 对于 $V (Y_{i}) (i = 1, 2, \dots, k)$ 中的任一顶点和 $X_{> k}$ 中的任一顶点，交换 $X_{> k}$ 和 $Y_{> k}$ 的位置，两点之间的距离减少2i，则总的Wiener指数减少 $\sum_{i = 1}^{k} (2 i) | V (Y_{i}) | | V (X_{> k}) |$ ；

3) 对于 $V (Y_{i}) (i = 1, 2, \dots, k)$ 中的任一顶点和中的任一顶点，交换 $X_{> k}$ 和 $Y_{> k}$ 的位置，两点之间的距离减少2i，则总的Wiener指数减少 $\sum_{i = 1}^{k} (2 i) | V (Y_{i}) | | V (Y_{> k}) |$ ；

4) 对于 $V (X_{i}) (i = 1, 2, \dots, k)$ 中的任一顶点和 $Y_{> k}$ 中的任一顶点，交换 $X_{> k}$ 和 $Y_{> k}$ 的位置，两点之间的距离增加2i，则总的Wiener指数增加 $\sum_{i = 1}^{k} (2 i) | V (X_{i}) | | V (Y_{> k}) |$ ；

综上分析，交换 $X_{> k}$ 和 $Y_{> k}$ 的位置，得出 $W (T^{'}) - W (T) = \sum_{i = 1}^{k} 2 i (| V (X_{i}) | - | V (Y_{i}) |) (| V (X_{> k}) | - | V (Y_{> k}) |)$ 。

根据定理2.2，令 $C C_{T} (x) = \min_{v \in V (T)} C C_{T} (v)$ ，则 $x \in L (T)$ 。

情形1： $x \in V (X_{i}) (1 \leq i \leq k)$

此时， $D_{T^{'}} (x) - D_{T} (x) = 2 i (| V (X_{> k}) | - | V (Y_{> k}) |)$ ，利用引理2.1可得

$\begin{array}{l} C C_{T^{'}} (x) - C C_{T} (x) = 2 (W (T^{'}) - W (T)) - (D_{T^{'}} (x) - D_{T} (x)) \\ = 2 (| V (X_{> k}) | - | V (Y_{> k}) |) (\sum_{i = 1}^{k} 2 i (| V (X_{i}) | - | V (Y_{i}) |) - i) \\ \leq 2 (| V (X_{> k}) | - | V (Y_{> k}) |) \sum_{i = 1}^{k} (2 i (| V (X_{i}) | - | V (Y_{i}) |) - 1) \end{array}$

当 $| V (X_{i}) | = | V (Y_{i}) | (i = 1, 2, \dots, k)$ 时，交换 $X_{> k}$ 和 $Y_{> k}$ 的位置，覆盖成本不增加。

存在i使得 $| V (X_{i}) | > | V (Y_{i}) |$ ，则 $\sum_{i = 1}^{k} (2 i (| V (X_{i}) | - | V (Y_{i}) |) - 1) > 0$ ，

由假设 $| V (X_{> k}) | \leq | V (Y_{> k}) |$ ，可得出 $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

因为 $\min_{v \in V} C C_{T^{'}} (v) \leq C C_{T^{'}} (x) \leq C C_{T} (x) = \min_{v \in V} C C_{T} (v)$ ，所以，交换 $X_{> k}$ 和 $Y_{> k}$ 的位置，最小覆盖成本不增加。

情形2： $x \in V (Y_{i}) (1 \leq i \leq k)$ 与情形1类似。

情形3： $x \in V (X_{> k})$

这时， $D_{T^{'}} (x) - D_{T} (x) = \sum_{i = 1}^{k} 2 i (| V (X_{i}) | - | V (Y_{i}) |)$ ，

利用引理2.1化简可得 $C C_{T^{'}} (x) - C C_{T} (x) = \sum_{i = 1}^{k} 2 i (| V (X_{i}) | - | V (Y_{i}) |) (2 (| V (X_{> k}) | - | V (Y_{> k}) |) - 1)$ 。

由假设 $| V (X_{> k}) | \leq | V (Y_{> k}) |$ ，可得出 $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

因为 $\min_{v \in V} C C_{T^{'}} (v) \leq C C_{T^{'}} (x) \leq C C_{T} (x) = \min_{v \in V} C C_{T} (v)$ ，所以，交换 $X_{> k}$ 和 $Y_{> k}$ 的位置，最小覆盖

成本不增加。

情形4： $x \in V (Y_{> k})$ 与情形3类似。

情形5： $x \in V (Z)$ ， $D_{T^{'}} (x) = D_{T} (x)$ ， $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

综上所述，在理想树中满足 $| V (X_{> k}) | \geq | V (Y_{> k}) |$ ，定理证明完毕。

定理3.2. 在如上描述的情形中，对于 $i = 1, 2, \dots, k - 1$ ，有 $| V (X_{i}) | \geq | V (Y_{i}) |$ ， $| V (X_{> k}) | \geq | V (Y_{> k}) |$ ，则在理想树中满足 $| V (X_{k}) | \geq | V (Y_{k}) |$ 。

证明：假设在理想树中， $| V (X_{k}) | \geq | V (Y_{k}) |$ 不成立，下面证明交换 $X_{k}$ 和 $Y_{k}$ 的位置不会增加覆盖成本。

根据定理2.2，令 $C C_{T} (x) = \min_{v \in V (T)} C C_{T} (v)$ ，则 $x \in L (T)$ 。

经过计算得 $\begin{matrix} W (T^{'}) - W (T) = \sum_{i = 1}^{k - 1} 2 i (| V (X_{i}) | - | V (Y_{i}) |) (| V (X_{k}) | - | V (Y_{k}) |) \\ + 2 k (| V (X_{> k}) | - | V (Y_{> k}) |) (| V (X_{k}) | - | V (Y_{k}) |) \\ \leq 0 \end{matrix}$

情形1： $x \in V (X_{i}) (1 \leq i \leq k - 1)$

$\begin{matrix} C C_{T^{'}} (x) - C C_{T} (x) = \sum_{i = 1}^{k - 1} 4 i (| V (X_{i}) | - | V (Y_{i}) |) (| V (X_{k}) | - | V (Y_{k}) |) \\ + 4 k (| V (X_{> k}) | - | V (Y_{> k}) |) (| V (X_{k}) | - | V (Y_{k}) |) \\ - 2 i (| V (X_{k}) | - | V (Y_{k}) |) \end{matrix}$

由假设 $| V (X_{k}) | \leq | V (Y_{k}) |$ ，可得出 $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

因为 $\min_{v \in V} C C_{T^{'}} (v) \leq C C_{T^{'}} (x) \leq C C_{T} (x) = \min_{v \in V} C C_{T} (v)$ ，所以交换 $X_{k}$ 和 $Y_{k}$ 的位置，最小覆盖成本

不增加。

情形2： $x \in V (Y_{i}) (1 \leq i \leq k - 1)$ 与情形1类似。

情形3： $x \in V (X_{> k})$

$C C_{T^{'}} (x) - C C_{T} (x) = (\sum_{i = 1}^{k - 1} 4 i (| V (X_{i}) | - | V (Y_{i}) |) + 4 k (| V (X_{> k}) | - | V (Y_{> k}) |) - 2 k) (| V (X_{k}) | - | V (Y_{k}) |)$

由假设 $| V (X_{k}) | \leq | V (Y_{k}) |$ ，可得出 $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

又因为 $\min_{v \in V} C C_{T^{'}} (v) \leq C C_{T^{'}} (x) \leq C C_{T} (x) = \min_{v \in V} C C_{T} (v)$ ，所以交换 $X_{k}$ 和 $Y_{k}$ 的位置，最小覆盖成

本不增加。

情形4： $x \in V (Y_{> k})$ 与情形3类似。

情形5： $x \in V ( X k )$

$\begin{matrix} C C_{T^{'}} (x) - C C_{T} (x) = \sum_{i = 1}^{k - 1} (| V (X_{i}) | - | V (Y_{i}) |) (4 i (| V (X_{k}) | - | V (Y_{k}) |) - 1) \\ + (| V (X_{> k}) | - | V (Y_{> k}) |) (4 k (| V (X_{k}) | - | V (Y_{k}) |) - 1) \end{matrix}$

由假设 $| V (X_{k}) | \leq | V (Y_{k}) |$ ，可得出 $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

又因为 $\min_{v \in V} C C_{T^{'}} (v) \leq C C_{T^{'}} (x) \leq C C_{T} (x) = \min_{v \in V} C C_{T} (v)$ ，所以交换 $X_{k}$ 和 $Y_{k}$ 的位置，最小覆盖成

本不增加。

情形6： $x \in V (Y_{k})$ 与情形5类似。

情形7： $x \in V (Z)$ ， $D_{T^{'}} (x) = D_{T} (x)$ ， $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

综上所述，在理想树中满足 $| V (X_{k}) | \geq | V (Y_{k}) |$ ，定理证明完毕。

定理3.3. 在如上描述的情形中，对于 $i = 1, 2, \dots, k - 1$ ，如果有 $| V (X_{i}) | \geq | V (Y_{i}) |$ 和 $| V (X_{> k - 1}) | \geq | V (Y_{> k - 1}) |$ 成立，则在理想树中满足 $d (x_{k}) \geq d (y_{k})$ 。

证明：假设在理想树中 $d (x_{k}) \geq d (y_{k})$ 不成立，设 $a = d (x_{k}) < d (y_{k}) = a + b$ ，从 $X_{k} (Y_{k})$ 中移除顶点 $x_{k} (y_{k})$ 会产生 $a (a + b)$ 个分支。从 $Y_{k}$ 中任取b个分支(令B为b个分支)，将这些分支与顶点 $x_{k}$ 连接。经过此操作有 $d (x_{k}) \geq d (y_{k})$ ，且度序列不改变。

根据定理2.2令 $C C_{T} (x) = \min_{v \in V (T)} C C_{T} (v), x \in L (T)$ 。

计算得 $W (T^{'}) - W (T) = \sum_{i = 1}^{k - 1} 2 i (| V (Y_{i}) | - | V (X_{i}) |) | B | + 2 k (| V (Y_{> k - 1}) | - | B | - | V (X_{> k - 1}) |) | B |$

情形1： $x \in V (X_{i}) (1 \leq i \leq k - 1)$

$C C_{T^{'}} (x) - C C_{T} (x) = \sum_{i = 1}^{k - 1} 4 i (| V (Y_{i}) | - | V (X_{i}) |) | B | + 4 k (| V (Y_{> k - 1}) | - | B | - | V (X_{> k - 1}) |) | B | + 2 i | B |$

由已知可以得出 $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

因为 $\min_{v \in V} C C_{T^{'}} (v) \leq C C_{T^{'}} (x) \leq C C_{T} (x) = \min_{v \in V} C C_{T} (v)$ ，经过上面操作，最小覆盖成本不增加。

情形2： $x \in V (Y_{i}) (1 \leq i \leq k - 1)$ 与情形1类似。

情形3： $x \in V (Y_{> k - 1} - B)$

$C C_{T^{'}} (x) - C C_{T} (x) = \sum_{i = 1}^{k - 1} 4 i (| V (Y_{i}) | - | V (X_{i}) |) | B | + 4 k (| V (Y_{> k - 1}) | - | B | - | V (X_{> k - 1}) |) | B | - 2 k | B |$

由已知可以得出 $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

因为 $\min_{v \in V} C C_{T^{'}} (v) \leq C C_{T^{'}} (x) \leq C C_{T} (x) = \min_{v \in V} C C_{T} (v)$ ，所以经过上面操作，最小覆盖成本不增加。

情形4： $x \in V (X_{> k - 1})$ 与情形3类似。

情形5： $x \in V ( B )$

$\begin{matrix} C C_{T^{'}} (x) - C C_{T} (x) = \sum_{i = 1}^{k - 1} 4 i (| V (Y_{i}) | - | V (X_{i}) |) | B | + 4 k (| V (Y_{> k - 1}) | - | B | - | V (X_{> k - 1}) |) | B | \\ - \sum_{i = 1}^{k - 1} (2 i) (| V (Y_{i}) | - | V (X_{i}) |) - 2 k (| V (Y_{> k - 1}) | - | B | - | V (X_{> k - 1}) |) \end{matrix}$

由已知可以得出 $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

因为 $\min_{v \in V} C C_{T^{'}} (v) \leq C C_{T^{'}} (x) \leq C C_{T} (x) = \min_{v \in V} C C_{T} (v)$ ，所以经过上面操作，最小覆盖成本不增加。

情形6： $x \in V (Z)$ ， $D_{T^{'}} (x) = D_{T} (x)$ ， $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

综上所述，在理想树中满足 $d (x_{k}) \geq d (y_{k})$ ，定理证明完毕。

在理想树中选一条最长路，将各个顶点依次命名为 $w_{1}, w_{2}, \dots$ 和 $u_{1}, u_{2}, \dots$ ，将各个点所在的分支依次命名为 $W_{i}$ 和 $U_{i}$ ， $U_{1}$ 是拥有点数最多的分支。如图3所示。

Figure 3. The components resulted from a path

图3. 在路上的分支

定理3.4. 如上面所述，在理想树中，如果路长是奇数 $2 m - 1$ ，则有

$| V (U_{1}) | \geq | V (W_{1}) | \geq | V (U_{2}) | \geq | V (W_{2}) | \geq \dots \geq | V (U_{m}) | = | V (W_{m}) | = 1$ ;

如果路长是偶数2m，则有 $| V (U_{1}) | \geq | V (W_{1}) | \geq | V (U_{2}) | \geq | V (W_{2}) | \geq \dots \geq | V (W_{m}) | = | V (U_{m + 1}) | = 1$ ；

证明：本定理只证明路长为奇数，路长为偶数可类似证明。我们假设 $| V (U_{1}) | \geq | V (W_{1}) | \geq | V (U_{2}) |$ 。对

于某个k，我们可得

$| V (U_{1}) | \geq | V (W_{1}) | \geq | V (U_{2}) | \geq | V (W_{2}) | \geq \dots \geq | V (W_{k - 1}) | \geq | V (U_{k}) |$ (1)

如果(1)中除了 $| V (U_{k}) | \geq | V (W_{k}) |$ 其余都成立。我们可以交换 $W_{i}$ 和 $U_{i}$ 的命名去保证 $| V (U_{k}) | \geq | V (W_{k}) |$ (如果有必要)。否则，根据定理3.1可得 $| V (U_{> k - 1}) | \geq | V (W_{> k - 1}) |$ 。

如果 $| V (W_{k}) | \geq | V (U_{k}) |$ ，则可以得出

$| V (U_{> k}) | = | V (U_{> k - 1}) | - | V (U_{k}) | > | V (W_{> k - 1}) | - | V (W_{k}) | = | V (W_{> k}) |$

应用定理3.2 (令 $x_{i} = u_{i}, y_{i} = w_{i}, i = 1, 2, \dots$ )，由 $| V (U_{> k}) | \geq | V (W_{> k}) |$ ，会得出 $| V (U_{k}) | \geq | V (W_{k}) |$ ，与前面假设 $| V (W_{k}) | \geq | V (U_{k}) |$ 矛盾。因此，可以得出

$| V (U_{1}) | \geq | V (W_{1}) | \geq | V (U_{2}) | \geq | V (W_{2}) | \geq \dots \geq | V (U_{k}) | \geq | V (W_{k}) |$ .

如果所有的不等式成立，可以交换 $U_{i + 1}, W_{i}$ 去保证 $| V (W_{k}) | \geq | V (U_{k + 1}) |$ (如果有必要)。否则，对 $U_{> k}$ 和 $W_{> k - 1}$ 应用定理3.1，令 $Z = U_{1}, Y_{i} = U_{i + 1}, X_{i} = W_{i}, z = u_{1}, y_{i} = u_{i + 1}, x_{i} = w_{i}$ ，有 $| V (X_{i}) | \geq | V (Y_{i}) | (i = 1, 2, \dots, k - 1)$ ，由定理3.1可得

$| V (W_{> k - 1}) | = | V (X_{> k - 1}) | \geq | V (Y_{> k - 1}) | = | V (U_{> k}) |$

如果 $| V (Y_{k}) | = | V (U_{k + 1}) | > | V (W_{k}) | = | V (X_{k}) |$ ，则有

$| V (Y_{> k}) | = | V (Y_{> k - 1}) | - | V (Y_{k}) | < | V (X_{> k - 1}) | - | V (X_{k}) | = | V (X_{> k}) |$ ,

对 $Y_{k} = U_{k + 1}, X_{k} = W_{k}$ 应用定理3.2，可得 $| V (X_{k}) | > | V (Y_{k}) |$ ，与前面假设 $| V (Y_{k}) | > | V (X_{k}) |$ 矛盾，因此，有

$| V (U_{1}) | \geq | V (W_{1}) | \geq | V (U_{2}) | \geq | V (W_{2}) | \geq \dots \geq | V (U_{k}) | \geq | V (W_{k}) | \geq | V (U_{k + 1}) |$ .

定理3.5. 如上面所述，在理想树中，如果路长是奇数 $2 m - 1$ ，则有

$d (u_{1}) \geq d (w_{1}) \geq d (u_{2}) \geq d (w_{2}) \geq \dots \geq d (u_{m}) = d (w_{m}) = 1$ ;

如果路长是偶数2m，则有

$d (u_{1}) \geq d (w_{1}) \geq d (u_{2}) \geq d (w_{2}) \geq \dots \geq d (w_{m}) = d (u_{m + 1}) = 1$ ;

证明：本定理只证明路长为奇数，路长为偶数时可类似证明。对 $u_{i}, u_{i + 1} (i = 1, 2, \dots, m - 1)$ 应用定理3.3，令 $y_{1} = u_{i + 1}, y_{2} = u_{i + 2}, \dots; x_{1} = u_{i}, x_{2} = u_{i - 1}, \dots, x_{i} = u_{1}, x_{i + 1} = w_{1}$ 。则

$| V (X_{> 1}) | = \sum_{k = 1}^{m} | V (W_{k}) | + \sum_{k = 1}^{i - 1} | V (U_{k}) | > \sum_{k = i + 2}^{m} | V (U_{k}) | = V (Y_{> 1})$ ,

推出 $d (u_{i}) = d (x_{1}) \geq d (y_{1}) = d (u_{i + 1})$ 。因此，可以得出

$d (u_{1}) \geq d (u_{2}) \geq \dots \geq d (u_{m})$ .

同理，对 $w_{i}, w_{i + 1}$ 应用定理3.3，得出 $d (w_{1}) \geq d (w_{2}) \geq \dots \geq d (w_{m})$ 。

对于 $u_{i}, w_{i}$ ，如果定理3.4中的不等式处处成立，可得 $d (u_{i}) \geq d (w_{i}) (i = 1, 2, \dots, m)$ 。否则，给 $u_{i}, w_{i}$ 应用定理3.3(令 $x_{i} = u_{i}, y_{i} = w_{i}, i = 1, 2, \dots$ )得出 $d (u_{i}) \geq d (w_{i}) (i = 1, 2, \dots, m)$ 。

相似的，给 $w_{i}, u_{i + 1}$ 应用定理3.3，得出 $d (w_{i}) \geq d (u_{i + 1}) (i = 1, 2, \dots, m - 1)$ 。

定理3.6. 具有最小覆盖成本的树是贪婪树。

证明：在任意一条路中， $D_{T} (v)$ 只在一个顶点或者两个相邻的顶点取到最小值，称这些点为重心。在定理3.4，3.5的理想树中的任意一条路上， $D_{T} (v)$ 在 $u_{1}$ 处取到最小值， $d (u_{1})$ 和 $| V (U_{1}) |$ 在这条路上都是最大的。

下面有两种情况：

1) 如果重心为一个点，则命名为v。

2) 如果重心为两个点，则两个分支(移除两个顶点之间的边)有相同的顶点数。选择其中一个顶点命名为v，另一个命名为 $v_{1}$ ，

本文只证明第一种情况，第二种情况证明类似。

在以顶点v为根的理想树 $(T, v)$ 中，很容易得出v是具有最大度的顶点。(引理2.3中(1)满足)

考虑任意一条以叶子点u开始，经过顶点v，以叶子点w结束(w和u有唯一相同的前序点v)的路，在这条路上应用定理3.5，使 $u_{1} = v$ ，可以得出

$| d_{T} (u, v) - d_{T} (w, v) | \leq 1$ ，即任意两个叶子点的高度差至多是1。(引理2.3中(2)满足)

并且，可以推出对于任意两个顶点 $x, y$ (y是x的后序点)，都有 $d (x) \geq d (y)$ 。

对于高度为i的顶点x和高度为j的顶点y ( $i < j$ )，考虑下面两种情况：

a) 如果y是x的后序点，可直接由上面得出 $d (x) \geq d ( y )$

b) 否则，令u为 $x, y$ 共同的前序点，且顶点u在 $P_{T} (x, y)$ 上。在通过顶点 $y^{'}, y, u, x, x^{'}$ 的路上应用定理3.5 ( $y^{'}, x^{'}$ 分别为 $y, x$ 的后序点，且为叶子点)，有 $u_{1} = u$ ，由定理3.4可知

$x = u_{k + 1}, y = w_{l}$ 或者 $x = w_{k}, y = u_{l + 1}, (k = i - h_{T} (u), l = j - h_{T} (u), k + 1 \leq l)$ ，

根据定理3.5可推出 $d (x) \geq d (y)$ 。(引理2.3中(3)满足)

对于两个相同高度的非叶子点 $x, y$ ，满足 $d (x) \geq d (y)$ 。 $y^{'}, x^{'}$ 分别为 $y, x$ 的后序点，在通过顶点 $y^{'}, y, u, x, x^{'}$ 的最长路上应用定理3.5 (u为 $x, y$ 共同的前序点，且顶点u在 $P_{T} (x, y)$ 上)，有 $u_{1} = u$ ，根据定理3.4有，

$x = w_{k}, x^{'} = w_{l}, y = u_{k + 1}, y^{'} = u_{l + 1}, (k = i - h_{T} (u), l = j - h_{T} (u))$ ,

因此可以推出

$d (x^{'}) \geq d (y^{'})$ 。(引理2.3中(4)满足)

令 $x_{0} (x^{'}), y_{0} (y^{'})$ 分别为 $x, y$ 的parents (siblings)，令 $y^{″}, x^{″}$ (高度为j)分别为 $y^{'}, x^{'}$ 的后序点，由结论(4)可推出 $| V (T (x_{0}) / T (x^{'})) | > | V (T (y_{0}) / T (y^{'})) |$ 。现在考虑经过顶点 $y^{″}, y^{'}, u, x^{'}, x^{″}$ 的最长路，u为 $x, y$ 共同的前序点且顶点u在 $P_{T} (x, y)$ 上，应用定理3.5则有 $u_{1} = u$ ，由定理3.5有 $x^{'} = w_{k}, x^{″} = w_{l}, y^{'} = u_{k + 1}, y^{″} = u_{l + 1}, (k = i - h_{T} (u), l = j - h_{T} (u))$ ，

因此可以推出

$d (x^{'}) \geq d (y^{'}), d (x^{″}) \geq d (y^{″})$ 。(引理2.3中(5)满足)

从而覆盖成本最小的树是贪婪树，即理想树是贪婪树，定理证明完毕。

例2．度序列为 $(4, 4, 3, 3, 3, 3, 2, 2, 1, \dots, 1)$ (1的重数为10)时，覆盖成本最小的树即贪婪树，如图4所示。

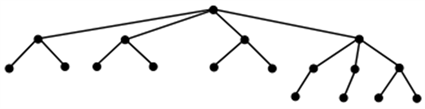
Figure 4. Greedy tree with degree sequence of (4,4,3,3,3,3,2,2,1,…,1)

图4. 度序列为(4,4,3,3,3,3,2,2,1,…,1)的贪婪树

文章引用

贾雁宇,李玉瑛,郝艺方. 给定度序列具有最小覆盖成本的树
The Minimum Cover Cost of a Tree with Given Degree Sequence[J]. 应用数学进展, 2021, 10(07): 2605-2613. https://doi.org/10.12677/AAM.2021.107270

参考文献

1. Fischermann, M., Hoffmann, A., Rautenbach, D., Székely, L. and Volkmann, L. (2002) Wiener Index versus Maximum Degree in Trees. Discrete Applied Mathematics, 122, 127-137.

2. Wang, H. (2008) The Extremal Values of the Wiener Index of a Tree with Given Degree Sequence. Discrete Applied Mathematics, 156, 2647-2654.

3. Zhang, X.D., Xiang, Q.Y., Xu, L.Q. and Pan, R.Y. (2008) The Wiener Index of Trees with Given Degree Sequences. Match-Communications in Mathematical and in Computer Chemistry, 60, 623-644.

4. Georgakopoulos, A. (2012) A Tractable Variant of Cover Time. arXiv:1206.6605.

5. Georgakopoulos, A. and Wagner, S. (2017) Hitting Times, Cover Cost, and the Wiener Index of a Tree. Journal of Graph Theory, 84, 311-326.

6. Li, S.C. and Wang, S.J. (2020) Extremal Cover Cost and Reverse Cover Cost of Trees with Given Segment Sequence. Discrete Mathematics, 343, 111791.

7. Zhang, H.H. and Li, S.C. (2021) On the (Reverse) Cover Cost of Trees with Some Given Parameters. Discrete Mathematics, 344, 112226.

NOTES

^*通讯作者。

期刊菜单