Advances in Applied Mathematics
Vol.
11
No.
01
(
2022
), Article ID:
48329
,
7
pages
10.12677/AAM.2022.111037
三类典型数理方程的数值解方法探析
朱起源
重庆科技学院数理与大数据学院,重庆
收稿日期:2021年12月24日;录用日期:2022年1月14日;发布日期:2022年1月26日

摘要
数学物理方程简称数理方程,主要指的是从具体物理问题中导出的偏微分方程。数理方程作为工科相关专业的一门专业基础课,掌握定解问题的数值求解方法对学生将来从事工程技术研究是非常必要的,而课程教学以求问题的解析解为主要内容。本文针对这一问题,以三类典型方程构成的定解问题为例,应用有限差分法讨论数值求解的思路和方法,以期能够作为主体教学内容的验证与拓展,起到启发解题思路的作用。
关键词
数理方程,数值方法,有限差分

Analysis on Numerical Solution Methods of Three Typical Mathematical Equations
Qiyuan Zhu
School of Mathematics, Physics and Big Data, Chongqing University of Science and Technology, Chongqing
Received: Dec. 24th, 2021; accepted: Jan. 14th, 2022; published: Jan. 26th, 2022

ABSTRACT
Mathematical equations mainly refer to the partial equations derived from physical problems. As a professional basic course of engineering related majors, mastering the numerical solution method is necessary for students to pursue their careers. However, the main content of the course is the analytic method. Therefore, three kinds of typical equations are taken as examples, to discuss the ideas and methods of numerical solution by using the finite difference method. As verification and expansion of the main content of teaching, it is hoped to play an enlightening role in solving problems.
Keywords:Mathematical Equations, Numerical Methods, Finite Difference

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
数理方程这门课开设的目的在于培养学生运用数学思想和数学知识分析和解决实际问题的能力,但由于数理方程构成的定解问题求解方法多样,计算过程复杂且对数学功底的要求很高 [1],因此在授课和学习过程中均存在一定的难度 [2]。工程实际中的绝大部分定解问题没有适定的解析解,另外工程师关注的是某些特定点处的函数值,而非具体的解析解。因此在课堂教学过程中,适当弱化繁琐的理论求解过程,同时重视数学建模 [3] 和数值求解能力的培养是非常必要的。例如2020年全国大学生数学建模竞赛中的A题炉温曲线,其本质就是求解扩散方程构成的定解问题。但如果不具备建模和数值求解能力的话,赛题是没办法解答的。本文针对课程教学过程中欠缺对数值求解能力培养的问题,采用有限差分方法,以扩散方程、波动方程和场位方程构成的定解问题为例,系统阐述问题求解的思路和方法。
2. 一维扩散方程构成的定解问题
首先考虑扩散方程构成的定解问题:
(1)
将偏导数的差分公式
,
代入扩散方程并整理得
令 ,,,,上式可写为下标形式,即
(2)
整理得
(3)
公式(3)即为一维扩散方程的显式差分公式,其中稳定条件是 ,截断误差为 。公式表明,j + 1时间层的数据可由第j时间层的值确定,其中第0时间层的数据就是定解问题中的初始条件 。因此基于显式差分公式,可以采用逐层向上递推的方式求解。
如果将扩散方程中二阶偏导项取 时刻的差分公式计算,则可得
(4)
整理得
(5)
公式(5)即为一维扩散方程的隐式差分公式,可以看出,第j时间层的数据是由第j + 1时间层的值表示的,因此无法继续使用逐层递推的方法求解。但(5)式给出了相邻时间层节点间满足的关系,因此可将相关节点间满足的关系式列出,联立求解方程组。联立得到的方程组可由以下矩阵方程简单表出
可以发现,系数矩阵中非零元集中分布在主对角线及相邻两对角线上,称为三对角矩阵,上述方程组也称为三对角方程组,第0个时间层的数据由初始条件给出,非齐次项中的 由边界条件给出。已知系数矩阵和非齐次项,求解未知向量的过程,即由第j时间层求第j + 1时间层数据的过程。为避免内存浪费,可以采用追赶法求解此类方程组 [4]。
如果将显示差分公式(2)和隐式差分公式(4)结合并整理得
(6)
公式(6)为平均隐式差分公式,也称Crank-Nicolson公式,具有六点对称的格式。可以证明,基于这个公式求解对任意步长都是稳定的。设
,
,
则相邻时间层节点间满足的方程组可由下述矩阵方程简单表示
(7)
由公式(7)可知,根据边界条件 ,已知第j个时间层数据 的情况下,类似地也可由追赶法求得第j + 1个时间层的值。
为了方便数值计算,设定解问题中
在进行网格剖分时,令 ,。由分离变量法可求得此定解问题的解析解为
图1表示在 时刻函数 在不同x处的值。红色虚线是基于级数形式的解析解得到的,在具体计算时选取的是前2000项的叠加结果。不同图形表示的离散点则是分别基于显式差分公式(3)、隐式差分公式(5)和平均隐式差分公式(6)经过数值计算得到的。可以看出,在选定的网格剖分情况下,基于不同差分公式求得的数值结果差别非常小,并且可以完全反映解析值。
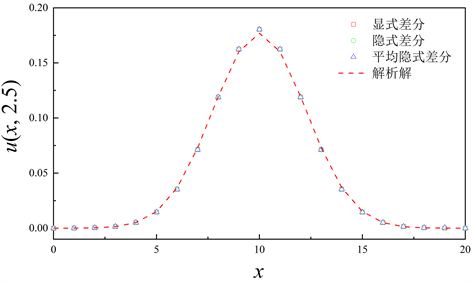
Figure 1. Comparison of numerical solutions based on different difference formulas and analytical solutions at t = 2.5
图1. t = 2.5时刻,基于不同差分公式得到的数值解与解析解的对比
3. 一维波动方程构成的定解问题
考虑由一维波动方程构成的定解问题
(8)
仿照前述做法,波动方程的差分格式可写为
令
上式也可写为下标形式。整理得
(9)
公式(9)即为一维波动方程的显式差分公式。可以看出,第j + 1个时间层的值由第j和j − 1个时间层的数据共同决定。利用定解问题中给定的初始条件,设初始时刻对应 ,将初位移和初速度离散化后,得第1个时间层数据 。利用速度的中心差分公式得 ,然后替换(9)式中的最后一项,整理得第2个时间层数据 。将前两个时间层的数据作为启动值,向上逐层求解即可。可以证明当 时,解是稳定的;当 时,可得正确的解析解;当 时,解是不稳定的。同样也可以导出隐式差分公式,但基于隐式差分公式的求解过程比较复杂,在此不再赘述。
由分离变量法可知,此问题的解析解为
其中 。为了数值计算方便,设 。
令
,
图2表示,在4个典型时刻 ,函数在不同x处波动状态的图像。其中绿色空心圆代表的是基于显式差分公式(9)求得的一系列离散值,黑色虚线表示基于此问题级数形式的解析解,选取前1000项求得的结果。可以发现在不同时刻,数值结果均能较好地反映解析数据规律。
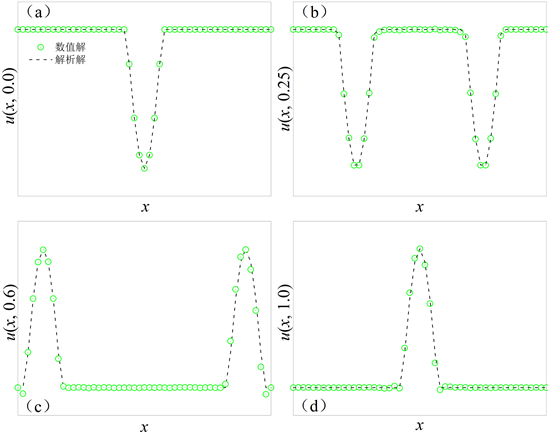
Figure 2. Comparison of wave states obtained by numerical method and analytic formula at t = 0, 0.25, 0.6 and 1.0
图2. t = 0, 0.25, 0.6, 1.0四个时刻,数值方法和解析式得到的波动状态对比
4. 二维场位方程构成的定解问题
考虑由二维场位方程构成的定解问题
(8)
利用二阶导数的中心差分公式,可得方程的差分形式 取 ,即 ,,。整理得显式差分公式
(9)
由上式可知,第 格点处的值由最近邻四个格点位置处的值所确定。将所有待求格点满足的方程联立构成方程组,原则上可以借助数学软件直接通过矩阵左除指令求解,但如果格点剖分太多,直接求解方程组需要较大内存,因此可以采用松弛迭代法进行数值求解 [5]。即随时用上一步计算得到的各点新值替代旧值,并且每次计算新值也替换成新值与旧值的“组合”。引入松弛因子,差分公式(9)的松弛迭代公式为
(10)
为保证迭代过程收敛,必须要求松弛因子 ,当 时称作低松弛法, 时称为超松弛法, 时,即公式(9)称为高斯–赛德尔迭代法。在迭代开始前,首先设定待求区域内各格点处的初始值作为迭代的启动值,然后基于式(10)逐次迭代求解。当前后两次迭代误差非常小时,即迭代收敛时可认为求得的数据接近真实值。类似地也可推导得出二维场位方程的隐式差分公式,这里也不再赘述。
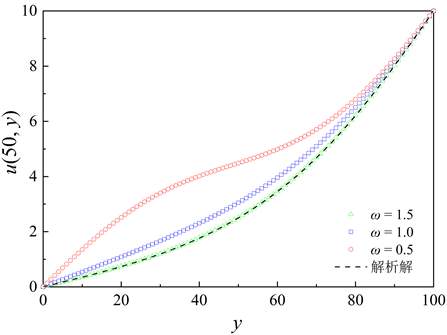
Figure 3. In the case of different relaxation factors, the function value at x = 50 (i.e. the position of the white dotted line in the illustration) was calculated with respect to y after 2000 iterations. The inset shows the distribution of the function u(x, y) after iterative convergence
图3. 取不同松弛因子的情况下,迭代计算2000次之后x = 50处(即插图中白色虚线位置)函数值随y的变化关系。插图表示迭代收敛时函数u(x, y)在平面内的分布规律
由分离变量法可得,此定解问题的解析解为 ,其中 。在进行数值计算时,首先按 进行网格剖分。然后根据边界条件设定待求解区域格点的初始值为5,最后分别取松弛因子 进行迭代求解。图3插图表示迭代收敛时函数在平面内的分布规律。取插图中白色虚线上函数值作为对比研究对象,由于下边界设定的值为0,上边界设定的值为10,因此沿白色虚线由下边界至上边界函数值由0递增至10。黑色虚线上的数据是取级数解中前130项计算得到的,描述的正是此递增规律。图中不同形状图形描述的是取不同松弛因子时迭代2000次得到的结果。可以看出当选择超松弛迭代法时,收敛速度最快,且迭代2000次之后已经与解析结果基本一致。另外,除松弛因子外,初始值的选取也会影响收敛速度,在这里不再详细讨论。
5. 总结
本文基于有限差分法,以三类典型数理方程构成的定解问题为例,详细论述了数值化的思路,并进一步基于差分公式讨论了数值求解的方法和步骤,最后将数值解和解析解进行对比分析,验证了数值方法的可行性和有效性。可以发现,针对不同类型方程构成的定解问题,差分方法的基本思路都是相同的,即将微分方程离散转化为一系列代数方程构成方程组,然后根据方程组的特点,综合考虑计算效率和计算机内存消耗选择具体的计算方法求解。这里只选取了三类典型方程构成的简单定解问题的求解方法,实际上,方程本身可以是非齐次的,并且定解条件也可能是其它更复杂的情形 [6]。这些问题只需要依据上述基本思路再做详细讨论即可。本文作为数学物理方程课程教学的有效补充,可以起到由理论到实际的桥梁作用,降低学生利用理论知识解决实际问题的门槛。
基金项目
重庆科技学院引进人才科研启动项目经费(ckrc2019017)。
文章引用
朱起源. 三类典型数理方程的数值解方法探析
Analysis on Numerical Solution Methods of Three Typical Mathematical Equations[J]. 应用数学进展, 2022, 11(01): 302-308. https://doi.org/10.12677/AAM.2022.111037
参考文献
- 1. 张静, 张彦, 唐琼, 等. “数学物理方法”课程改革的探索[J]. 大学教育, 2014(16): 163-165.
- 2. 王正斌, 毛巍威, 杨志红. “数理方程”课程教学改革探索[J]. 宜春学院学报(自然科学), 2006, 28(6): 51-52.
- 3. 刘鹏飞, 高博. 数学建模思想在数理方程教学中的渗透[J]. 吉林师范大学学报(自然科学版), 2007, 4(4): 132-133.
- 4. 吕同富, 康兆敏, 方秀男. 数值计算方法[M]. 第2版. 北京: 清华大学出版社, 2013: 86.
- 5. 彭芳麟. 计算物理基础[M]. 北京: 高等教育出版社, 2010: 346.
- 6. 胡其华, 熊建明. 数理方程动边界问题研究的发展状况与主要研究方法[J]. 九江学院学报(自然科学版), 2005, 2(2): 87-89.