 Computer Science and Applicatio n 计算机科学与应用, 2011, 1, 118-122 http://dx.doi.org/10.12677/csa.2011.13024 Published Online December 2011 (http://www.hanspub.org/journal/csa) Copyright © 2011 Hanspub CSA Experimental Study of Rolling Bearing Fault Diagnosis Technology Shuyong Liu, Liang Deng, Yo ng xi a n g Z han g Ship Structure and Power College, Naval University of Engineering, Wuhan Email: lsydh@sina.com Received: Oct. 6th, 2011; revised: Oct. 27th, 2011; accepted: N o v. 15th, 2011. Abstract: The rolling bearing is an important part in equipment. It is significant to research the diagnosis technology of the bearing in practical engineering. The combination of fractal diagnosis and characteristic frequency is presented in this paper, and the fault was determined on the basis of analyzing the vibration signal. The experimental structure an d measuring program are designed, and an intellig ent d iag nosis system is finished. Expe rimental results show th at the fractal dimensio n is increased wh en the fau lt occurs, an d the fault location is identified by the intelligent diagnosis system. Keywords: Rolling Element Bearing; Fault; Experimental Study 滚动轴承故障综合诊断试验研究 刘树勇,邓 亮,张永祥 海军工程大学船舶与动力学院,武汉 Email: lsydh@sina.com 收稿日期:2011 年10 月6日;修回日期:2011 年10 月27 日;录用日期:2011 年11 月15 日 摘 要:滚动轴承是机械设备中非常重要的部件,如何有效地实施滚动轴承故障诊断是值得深入研究 的问题。本文提出轴承分形理论和故障特征频率综合诊断法,通过对轴承振动信号进行分析实现其故 障诊断。设计了试验台架和振动测试方案,研制了基于故障特征频率的智能诊断系统。试验结果表明, 当滚动轴承出现故障时,振动信号分形维数明显增加,同时综合应用智能诊断系统识别了轴承的故障 部位。 关键词:滚动轴承;故障;试验研究 1. 引言 滚动轴承是机械设备中的重要部件之一,如舰用 柴油机、齿轮箱、滑油泵等设备中都使用了滚动轴承。 然而,滚动轴承由于其设计制造存在误差、使用安装 不合理以及长时间运行等原因,会出现不同形式的故 障,如疲劳剥落、磨损、塑性变形、腐蚀、断裂、胶 合等。如何有效地提取滚动轴承的故障信号,对滚动 轴承的状态进行评价以及根据测试信号进行滚动轴承 故障诊断一直是机械设备状态监测与诊断领域中的热 点和难点问题。除了传统的共振解调[1]方法以外,还 有很多学者进行了其他方法的研究。如李风英等人研 究了滚动轴承声发射检测技术,探讨了滚动轴承声发 射信号的采集处理以及诊断方法的特点[2],随后郝如 江等人对滚动轴承故障的声发射检测技术进行了综述 [3]。进行了研究。王小卉等人则采用二阶循环平稳分 析方法对滚动轴承故障提取方法进行研究[4]。分析了 循环自相关和循环谱密度的各种谱图,提出了切片集 合分析方法,提高了分析的可靠性,减少计算量,有 效地排除了故障干扰频率。此外,一些神经网络方法 也用于对滚动轴承故障模式进行识别[5]。随着混沌理 论的深入研究,分形技术在工程实际中得到了广泛的 应用。国内外已将分形理论用于滚动轴承故障诊断[6,7] 和齿轮的故障诊断[8],发现故障对分形维数值有一定  刘树勇 等 滚动轴承故障综合诊断试验研究 119 的影响。同时,在实际应用过程中,考虑到噪声的污 染,采用了小波包降噪技术。这些研究促进了设备状 态监测与故障诊断方法的发展。本文综合利用分形诊 断理论以及轴承故障诊断系统,对轴承故障进行了精 密诊断。 2. 滚动轴承振动机理 滚动轴承在工作时,外圈与轴承座或机壳相联接, 固定或相对固定;内圈与机械传动轴相联接,随轴一起 转动。在机械设备运转时,滚动体便在轴承内、外圈滚 道上滚动,由于本身结构的原因,每个滚动轴承在不同 位置会承受不同的交变载荷,而且承受载荷的滚动体数 量是不同的,这种承载刚度的变化必然会引起轴承产生 振动。另外,在加工过程中,内外轨道表明的粗糙程度、 波纹度以及形位误差等原因产生交变激励力也会使轴 承产生振动。虽然这些加工装配因素造成的激励力大多 具有周期性的特点,但由于实际构成因素十分复杂,各 因素之间也不存在特定的关系。所以,总体上而言这些 激振力随机性较强,含有多种频率成份。因而轴承系统 在这些激振力的作用下所产生的振动当然也具有多种 频率成分并具有较强的随机性。 更为重要的是,当轴承出现故障时更容易导致异 常振动的产生。在工程实际中主要包括两类故障,一 类是由于磨损产生的振动,一类是由于疲劳剥落、点 蚀等产生的振动。对于前者,其振动特征主要体现在 振幅增加。对于后一类故障,其振动特点是使系统产 生高频的固有振动。这一故障信号和其他信号混合在 一起,且由于其能量非常低,因此传统的方法难以提 取其故障特征。共振解调方法的研究为该问题提供了 强有力的手段。但工程界中通常容易忽略这样一个事 实,即滚动轴承在实际运转过程中,由于结构等非线 性因素的存在,不可避免地产生非线性振动。如何应 用非线性时间序列分析方法来处理这些振动信号也是 值得探讨的重要问题。本文应用分形维计算方法来分 析实际滚动轴承振动信号,为轴承故障诊断提供有效 参考。 3. 分形维数计算 根据非线性动力学理论可知非线性动力学系统的 行为在相空间体现为有序结构。虽然在时域或频域很 难发现这种有序性,但在相空间中可以观察到吸引子 的分形结构。在具有分形性质的吸引子上任选择一个 局部区域,由于其自身具有自相似性,对它进行放大 后,得到的图形会显示出与原图类似的特性,即它的 形态、不规则性和复杂程度等各种性质与原图相比均 不会发生变化,这种特性称为无标度性。相似性具有 层次结构上的差异,数学中的分形具有无穷嵌套的层 次结构,而自然界的分形只有有限层次的嵌套,而且 要进入到一定的层次结构后才有分形的规律。自然界 的分形通常具有一个最小标度和最大标度,在此区间 内才存在标度不变性。在实际中一般可以通过经典的 G-P 算法计算混沌吸引的关联维数,其主要特征是对 吸引子的不均匀性反应敏感,能够反映吸引子的静态 结构,同时它的物理意义非常明确。G-P 算法的主要 思想是先统计不同半径小球内的点数,然后通过关联 积分和半径之间的双对数曲线的斜率来确定关联维 数。 根据关联维数的计算方法,通常采用下式进行计 算: 22 11 NN NN ij ij ii ij CrrYYr r NN (1) 式中, Cr表示距离小于 r的点对在所有点对 中所占的比例, ij r 1 N rNCr r; x 是 Heaviside 函数: 1, 0 0, 0 ij ij ij rr rr rr 当时 当时 (2) 从(2)式中可以看出实际系统对 r的要求。值太 大或者太小两种情况都不能反映系统内部的性质。如 果的取值太大,那么所有点对之间的距离都不会 超过 ,这时 r rij r r 1 Nr Nr,,取对数后 Cr 1 Crln 0 ,这样的值当然反映不了系统内部的性质, 没有任何意义。如果 的值取得太小,那么所有点对 之间的距离都将大于 ,这时 ,于是 r ij r r Nr 10 Cr 0 。这样的 r值也反映不出系统内部的性质, 也没有意义。只有 ln lnCrr曲线的中间一段,r值 才对应无标度区,才能够反映系统的分形性质。 4. 滚动轴承故障诊断试验 4.1. 试验台组成 滚动轴承故障诊断试验台如图 1所示。主要由滚 Copyright © 2011 Hanspub CSA  刘树勇 等 滚动轴承故障综合诊断试验研究 120 Figure 1. Basic structure of experimental rig 图1. 实验台的基本结构 动轴承(型号 6004)、齿轮、电机、滑油泵等部分组成。 其工作原理是电机通过弹性连轴节带动齿轮运转,滚 动轴承安装在齿轮箱上,齿轮箱输出端通过连轴节和 滑油泵连接。试验过程中,主要采用有故障和无故障 两种滚动轴承进行振动测试。故障的模拟主要采用线 切割方法在外环滚道或者内环滚道上线切割一道故障 痕,测点的布置如图2所示。 4.2. 试验流程 滚动轴承故障诊断试验流程图如图 3所示,主要 包括信号采集、信号调理、故障特征频率的提取以及 计算信号的关联维数,对轴承故障进行诊断。当轴承 未出现故障时,对其工作状态进行评估或者对未来的 工作状态进行预测,当轴承出现故障时,对其原因进 行分析,判断故障的部位和严重程度。因此,轴承故 障诊断的主要研究内容包括测试方法的研究、状态评 估方法的研究和故障诊断预测等等。 4.3. 数据采集与分析 1) 智能诊断系统的应用。为了测试滚动轴承的振 动信号,采用了压电式加速度传感器测量其振动加速 度。在进行电机启动前的盘车检查后,给系统通电。 应用光电转速传感器测量其转速为2920 rpm。由于故 障特征频率处于低频阶段,设置采样频率为 3000 Hz, 足以包含所要分析的故障特征频率成分。采用自研的 轴承故障诊断系统对信号进行采集,如图 4所示,通 过调用智能处理程序可以得到的部分诊断结果如图 5 所示。频谱图中在约263 Hz位置的能量非常突出,为 故障特征频率。结合该型滚动轴承几何参数和运动参 数,应用故障特征频率计算公式,不难计算出外圈、 内圈以及滚动体等故障特征频率的具体数值。将该数 值263.866 Hz和频谱图比较,就可以推断出滚动轴承 内圈出现了故障,这和试验模拟的故障位置是吻合的。 2) 分形计算的结果 采用式(2)计算无故障和有故障时振动信号的关 联维数曲线如图 6和图 7所示。通过无标度区间的斜 率计算,得到无故障时关联维数为0.692。有故障时, 根据测量的数据可以计算其关联维数为 1.712,即有故 障时分形维明显增加,这表明,故障出现时,其系统 的响应更加复杂。 5. 结论 滚动轴承在实际运转过程中,由于结构等非线性 因素的存在,不可避免地产生非线性振动。本文应用 非线性时间序列分析方法来提取轴承振动信号的分形 特征,为轴承分形诊断提供了重要参考,通过计算, 得到了试验轴承在不同状态下振动信号的关联维数。 发现它有故障时分形维明显增加。由于分形维数对吸 引子的不均匀性反应敏感,能够反映吸引子的内部结 构,这表明,当故障出现时,系统的响应更加复杂。 同时,综合应用基于轴承故障特征频率分析研制的滚 动轴承故障智能诊断系统,可以对轴承的故障大小、 故障部位进行诊断。 Figure 2. The location of vibration sensor 图2. 传感器的布置 Copyright © 2011 Hanspub CSA 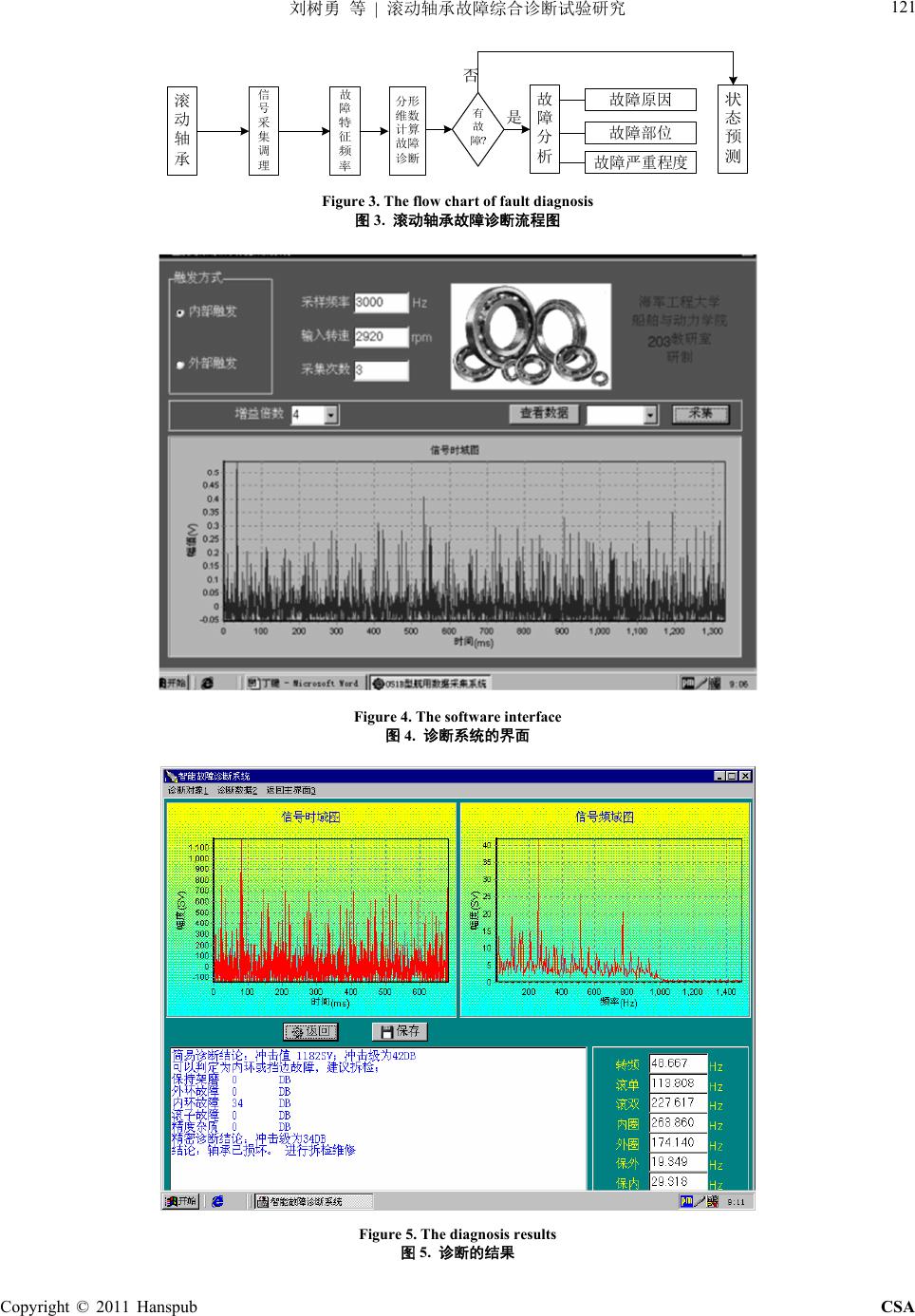 刘树勇 等 滚动轴承故障综合诊断试验研究 Copyright © 2011 Hanspub CSA 121 Figure 3. The flow chart of fault diagnosis 图3. 滚动轴承故障诊断流程图 Figure 4. The software interface 图4. 诊断系统的界面 Figure 5. The diagnosis results 图5. 诊断的结果 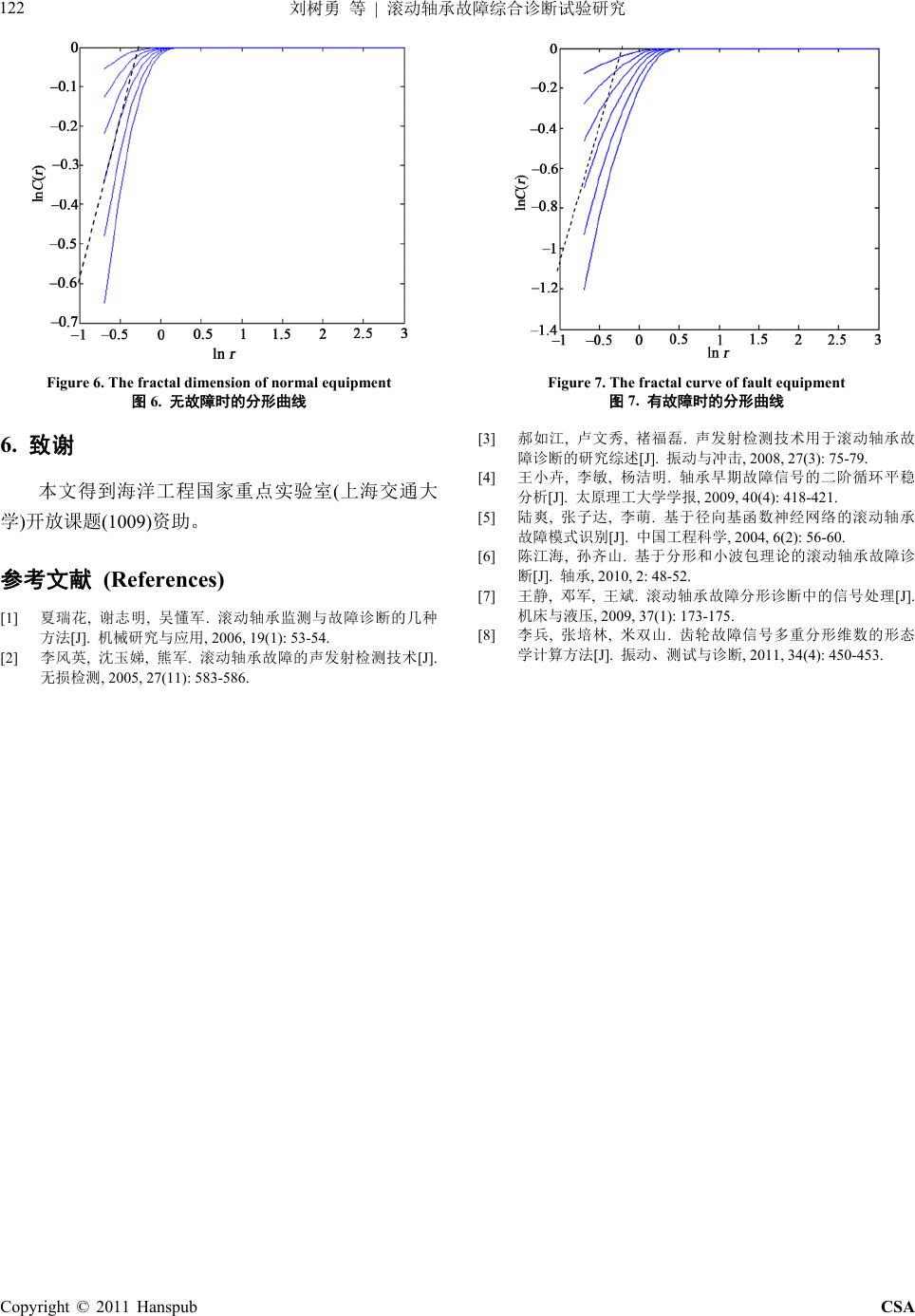 刘树勇 等 滚动轴承故障综合诊断试验研究 Copyright © 2011 Hanspub CSA 122 Figure 6. The fractal dimension of normal equipment 图6. 无故障时的分形曲线 Figure 7. The fractal curve of fault equipment 图7. 有故障时的分形曲线 6. 致谢 本文得到海洋工程国家重点实验室(上海交通大 学)开放课题(1009)资助。 参考文献 (References) [1] 夏瑞花, 谢志明, 吴懂军. 滚动轴承监测与故障诊断的几种 方法[J]. 机械研究与应用, 2006, 19(1): 53-54. [2] 李风英, 沈玉娣, 熊军. 滚动轴承故障的声发射检测技术[J]. 无损检测, 2005, 27(11): 583-586. [3] 郝如江, 卢文秀, 褚福磊. 声发射检测技术用于滚动轴承故 障诊断的研究综述[J]. 振动与冲击, 2008, 27(3): 75-79. [4] 王小卉, 李敏, 杨洁明. 轴承早期故障信号的二阶循环平稳 分析[J]. 太原理工大学学报, 2009, 40(4): 418-421. [5] 陆爽, 张子达, 李萌. 基于径向基函数神经网络的滚动轴承 故障模式识别[J]. 中国工程科学, 2004, 6(2): 56-60. [6] 陈江海, 孙齐山. 基于分形和小波包理论的滚动轴承故障诊 断[J]. 轴承, 2010, 2: 48-52. [7] 王静, 邓军, 王斌. 滚动轴承故障分形诊断中的信号处理[J]. 机床与液压, 2009, 37(1): 173-175. [8] 李兵, 张培林, 米双山. 齿轮故障信号多重分形维数的形态 学计算方法[J]. 振动、测试与诊断, 2011, 34(4): 450-453. |