Pure Mathematics
Vol.
13
No.
04
(
2023
), Article ID:
64848
,
7
pages
10.12677/PM.2023.134115
含组合型GMWB条款的变额年金定价
宫晶,陈萍
南京理工大学数学与统计学院,江苏 南京
收稿日期:2023年3月20日;录用日期:2023年4月21日;发布日期:2023年4月28日

摘要
带有最低保障条款的变额年金是目前存在的商业年金中对养老金系统的最好补充。本文通过对现有最低保障类条款的结合,构造了在严重通货膨胀的当下更适合市场环境的组合型条款。本文在最低提款保障上添加了最低到期保障以及可随时退保的选择权,在无套利假设的前提下使用现金流法通过研究保险公司的可能性损失,在随机死亡率、随机利率、理性退保等假设下给出了公平费率的定价公式。运用蒙特卡洛法对保险公司的潜在损失和公平费率进行了模拟计算和敏感性分析,同时讨论了添加可提前退保权益对保险公司可能面对风险的影响。数值仿真结果说明了本文定价模型的稳定性和高效性。
关键词
变额年金,最低保障条款,随时退保

Pricing of Variable Annuities with Combined Guaranteed Minimum Withdrawal Benefit
Jing Gong, Ping Chen
School of Mathematics and Statistics, Nanjing University of Science and Technology, Nanjing Jiangsu
Received: Mar. 20th, 2023; accepted: Apr. 21st, 2023; published: Apr. 28th, 2023

ABSTRACT
Variable annuities with minimum guaranteed benefits are the best supplements to pension system among the current commercial annuities. This study builds a new guaranteed rider to fit the severe inflation by integrating the previous guaranteed minimum benefits. This paper adds the surrender option and the guaranteed minimum maturity benefit to the guaranteed minimum withdrawal benefit, as well as using the numéraire approach to price the fair premium by studying the potential loss of insurance company under the no-arbitrage hypothesis, with stochastic mortality and interest rate assumptions. Use Monte Carlo method to simulate and sensitivity analyze the potential loss of insurance company and fair rate and discuss the risk that insurance company may face with surrender option. The numerical results are consistent and efficient.
Keywords:Variable Annuity, Guaranteed Minimum Benefits, Random Surrender

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
年金最初是作为员工鼓励计划诞生的,是企业雇主为雇员的退休生活提供的保障,后来发展衍变出了和市场投资相关联的变额年金,作为国家养老金体系的补充而长期存在,以便更好的满足人们的保值、增值需求。变额年金比普通年金更受欢迎的原因在于其给了投保人享有更高市场收益的可能,而高收益则伴随着高风险,最低保障条款也就应运而生。现存的最低保障类条款主要包含最低到期保障(GMMB)、最低提款保障(GMWB)、最低死亡保障(GMDB)和最低收入保障(GMIB)。针对各类条款的研究已有很多,本文主要研究关于GMWB条款的定价。Huang等 [1] 将GMWB看作随机控制问题进行了定价研究,并在假设基础资产遵循跳扩散过程的条件下给出了快速收敛的迭代方案,其结果表明该方案较直接控制法有一定的优越性。Gudkov等 [2] 在随机利率、随机波动率、随机死亡率的前提下对GMWB进行定价,将估值问题表示为PDE形式,采用算子分裂法进行了数值求解,并对公平保费进行了敏感性分析。Costabile等 [3] 提出了一个带有GMWB的可变年金评估框架,在理性变额提款策略下从更现实的角度对可能导致投保人最优及次优提款的情形进行了分析,使用基于格近似的评估模型计算了GMWB的公平费用价格,在更现实背景下考虑投保人决策。
近年各国的老龄化程度日益加剧,据我国国家统计局公布数据显示2021年65岁及以上人口已经占全国人口总数的14.2%,出生率降至7.5%,老年抚养比高达20.8%。逐年加速的老龄化和越来越低的出生率导致我国养老保险体系急需商业年金的支撑,2022年我国已经正式开启了个人养老金制度。随着通货膨胀的加剧,单一的附加条款越来越无法满足人们的生活需求,在原有条款的基础上创新出更符合实际市场情况的新型条款迫在眉睫,组合原有条款就是尝试的第一步。Luo等 [4] 曾尝试结合GMWB和GMDB条款,并将投保人的最优提款行为作为最优随机控制问题来解决,其结论表明在同时考虑市场风险、死亡率风险和投保人行为时,很难给出变额年金的合理价格,尤其当合约期限较长时,无法将公平费率设定为其账户价值的任何比例,但这依然是对原有条款创新的初步尝试。随着保险市场的进一步发展,在已有产品的基础上叠加不同的最低保障可以丰富保险市场并为年金产品增添吸引力,是未来的大势所趋。
本文运用现金流法对含随时退保权益、最低提款和到期保障条款(GMWB + GMMB)的变额年金进行了定价研究,并给出了公平费率的解析表达式。并且本文采用Lee-Carter模型 [5] 、 [6] 模拟随机死亡率、CIR模型 [7] 描述随机利率、BS模型 [8] 表示投资账户的市场表现,用蒙特卡洛法进行了模拟仿真和敏感性分析。通过分析保险公司的预期潜在损失讨论了添加退保权益对其面临风险的影响,数值结果表明本文的方法高效且稳定。本文的结构如下。第二部分介绍了我们将使用的模型和基本假设。第三部分给出了组合条款在不可以提前退保和可以随时退保两种情形下的定价公式。第四部分用蒙特卡洛法进行了模拟仿真和敏感性分析。最后是结论部分。
2. 模型假设及理论基础
最低提款保障(GMWB)通常附加在年金的提款期内,是保障投保人在整个提款期内的累计提款额至少为其初始投资金额,单次提款额通常为其初始投入的固定比率,并在合约到期日可一次性取出其年金账户中的全部剩余金额。最低到期保障(GMMB)通常设置在积累期内,保障投保人在积累期结束时年金账户中的金额至少为其初始投入的最低增长。含有最低保障条款的变额年金通常包含三个账户:呈现给投保人的年金账户 ,记录投保人所持年金资产在t时刻的实际价值;与市场挂钩的投资账户 ,可视为由金融衍生品构成的基金账户在t时刻的价值,服从随机利率下的BS模型;以及体现t时刻最低保障剩余价值的保障账户 。本文主要考虑即时型年金,延期年金也易推广,增加积累期即可。合约总时长为T年,每年m个提款日,共有N次提款日 和N个缴费日 ,即 , 。为简化表达,后文中均用n代表 ,即 。在每个提款日三个账户的金额都会发生变化,分别用()−和()+表示提款时刻之前与之后的对应变量值。
假设投保人x岁时购买附加组合GMWB条款的年金产品,公平保费c为年金账户的固定比率,每期初单独缴纳或从其提取金额中扣除。买入时刻为0时刻,初始投入金额为 ,则 。由于考虑即时年金,本文将每两个提款日之间的小区间看作一个短期积累期,添加的GMMB条款则保障n时刻投保人年金账户中的金额至少是 时刻其保障账户中的金额,即 。确保了在保障账户被完全提取之前,投保人年金账户中的金额不会低于其初始投入的未提取部分,可以更好的满足投保人的保值增值需求。同时将每期提款额设定为其年金账户的一定比率w,本文将w设定为合约到期之前剩余提款次数的倒数,即 。每期可提取金额都会随市场波动,当其保障账户中的金额清零后仍可继续提取其投资账户中的金额,给投保人提供更多享受市场上行红利的机会,n时刻的提款金额为 ,累计提款额为 。其提款前后其保障账户的金额变化可表述为 , ,投资账户中的金额变化则可表述为 , 。
关于随时退保权益,首先本文假设投保人为理性投保人,退保时刻 均发生在提款日,且退保需缴纳违约提取金额的一定比率,即违约罚率 。本文将提前退保发生原因统归为两类,第一类为个人突发意外情况,情况发生时投保人退保;第二类为其累计提款额达到预设的退保上限,类似于向上看涨障碍期权,当累计提款额达到退保上线时投保人退保。同时假设两类退保情况相对独立,退保发生则保单终止,投保人既可节省时间成本、未来保费还可规避之后市场下行的潜在性损失。并且假设死亡和退保不会同时发生,若投保人在合约期内身故,则投保人并未提前退保,若投保人主动要求退保,则投保人退保前保持存活状态。图1描述了含组合型GMWB条款年金账户的现金流。
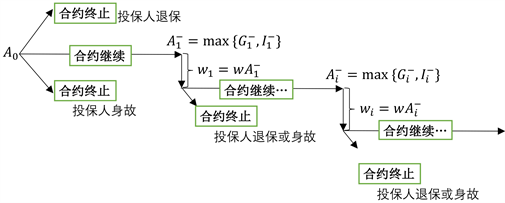
Figure 1. Cash flow of annuity account with combined GMWB
图1. 含组合型GMWB条款年金账户的现金流
3. 组合型GMWB条款的定价
年金类保险产品正常不允许提前退保,因为这会对保险公司的流动性现金流造成压力,为方便记述,本文将不可退保和含提前退保权益的年金合约分别记为合约A、B。先给出合约A的定价公式。
定理1不可提前退保的含GMWB + GMMB条款变额年金的公平费率 为
其中 为年龄为x岁的投保人在未来i年内的生存概率,r为年化利率。
证明 分析保险公司的现金流,其收入为每期收缴的保费,支出为每期市场可能性下滑导致的投资账户低于保障账户的部分,记保险公司预期损失在0时刻的贴现值为L0,假设投保人的死亡时刻为t,可得
由数学归纳法可得:
再由无套利原则,即 可得 。□
添加提前退保权益时,由于退保行为只能发生一次,可将其看作停时 ,则在第t个提款日发生退保的概率满足 ,由停时的特性可知
定理2含提前退保权益的GMWB + GMMB条款变额年金的公平费率 为
其中,
;
;
;
;
;
;
;
.
式中 为年龄为x岁的投保人在 时间内死亡的概率。
证明 仍从保险公司的角度在增加可提前退保权益后分析其现金流流入流出情况,可得在0时刻的预期损失贴现值为
通过添加死亡率和退保概率,用数学归纳法整合可得 ,由无套利原则可解 。□
4. 数值模拟
由于含有最低保障类条款,合约中涉及到的相关变量都有很强的路径依赖性,本文采用蒙特卡洛法在利率、死亡率均为随机模型的条件下对变额年金进行定价,利率模型参数采用美联储过去20年的历史数据生成,死亡率模型参数使用1950~2016年男性历史生存率数据生成。假定的两类退保情形中,第一类突发事件假设为癌症类重大疾病,使用WHO公布的每年新增癌症癌患病率数据进行模拟,第二类退保上线设定为预期最终收益的2倍,违约罚率 保险公司一般设定在5%~10%之间。本文模拟比较了不同投保年龄层、不同风险波动率、可否退保以及不同违约罚率对公平费率及保险公司可能性损失的影响。参数设定为 , , ,投资账户买入的风险资产初始价值 , ,模拟仿真过程均在风险中性测度 下进行,对 进行设定是由于退保上线与预期收益相关, 和55, 和10%,蒙特卡洛模拟104次。
由表1可以看出c和 、98%VaR、98%CTE等均与 有较强正相关性,而与x只存在微弱正相关趋势。由于在无套利原则下进行的定价,两类合约得到的预期损失期望都趋于0,但波动率的增大仍然加大了损失期望波动的幅度。且增加提前退保权益致使保险公司收取的违约金直接增加了其流动资金,反而补偿了部分流动性风险。数值模拟时间均在70 s左右,多次模拟得到的数据结果均在可信区间内波动,具有较好的稳定性。
表2展示了含退保权益单违约罚率不同的情形下价格的变动趋势。由仿真结果可知,仍是 与c和 呈显著正相关, 的变动对c仅有轻微影响, 的数据结果也具有相同变化趋势,在此不单独列表。由98%VaR和98%CTE数据可以看出,在本文包含的两类理性退保情况下发生的退保行为并不会给保险公司造成负担,甚至可以轻微降低保险公司为防范最低保障类条款带来的风险而预留的储备金。并不排除现实生活中会有其他种类的突发情况或仅是投保人因为信息不对等而不够理性,但由本文结果可知增加确定情形的随机退保选择权对保险公司和投保人均益大于弊。
Table 1. Simulation results when x = 45, 55 of contract A and contract B containing surrender right with κ = 5%
表1. 合约A和含退保权益且κ = 5%的合约B在x = 45和55时的模拟结果
Table 2. Simulation results when x = 45 of contract B containing surrender right with κ = 5%, 10%
表2. 含退保权益的合约B在x = 45,κ = 5%和10%时的模拟结果
5. 结语
本文是对传统最低保障条款的初步延展,在最低提款保障上添加了最低增长保障,并对可提前退保的情况进行了定性研究和数值模拟。在无套利假设的基础上,采用随机死亡率和随机利率,通过研究保险公司的可能损失给出了公平费率的定价公式,并用蒙特卡洛法进行了仿真模拟和敏感性分析,数值结果表明本文的定价模型高效、稳定。从数据结果可知公平保费、保险公司面临风险与投保年龄、投资组合的预期波动率之间呈正相关。通过对预期损失的98%CTE和98%VaR的分析表明增加退保权益对保险公司将面临的风险并没有太大影响,甚至可以轻微降低保险公司需为这类条款预留的储备金。
本文重点研究组合型条款公平费率的定价问题,因此在定价过程中不考虑手续费、管理费和其他费用以及通胀的影响,也不详细讨论风险资产的具体选择,直接将其投资账户看作是由金融衍生品构成的投资组合。本文中涉及的相关模型均可推广到其他的随机过程。本文研究了在即时型年金上组合附加了GMWB和GMMB条款的情形,也可以很容易的推广到延期型年金和其他的组合型条款上,之后也会进一步考虑风险对冲等问题。
文章引用
宫 晶,陈 萍. 含组合型GMWB条款的变额年金定价
Pricing of Variable Annuities with Combined Guaranteed Minimum Withdrawal Benefit[J]. 理论数学, 2023, 13(04): 1083-1089. https://doi.org/10.12677/PM.2023.134115
参考文献
- 1. Huang, Y., Forsyth, P.A. and Labahn, G. (2012) Iterative Methods for the Solution of a Singular Control Formulation of a GMWB Pricing Problem. Numerische Mathematik, 122, 133-167. https://doi.org/10.1007/s00211-012-0455-y
- 2. Gudkov, N., Ignatieva, K. and Ziveyi, J. (2019) Pricing of Guaranteed Minimum Withdrawal Benefits in Variable Annuities under Stochastic Volatility, Stochastic Interest Rates and Stochastic Mortality via the Componentwise Splitting Method. Quantitative Finance, 19, 501-518. https://doi.org/10.1080/14697688.2018.1490806
- 3. Costabile, M., Massabó, I. and Russo, E. (2020) Evaluating Variable Annuities with GMWB When Exogenous Factors Influence the Policy-Holder’s Withdrawals. The European Journal of Finance, 26, 238-257. https://doi.org/10.1080/1351847X.2019.1618362
- 4. Luo, X.L. and Shevchenko, P.V. (2015) Valuation of Var-iable Annuities with Guaranteed Minimum Withdrawal and Death Benefits via Stochastic Control Optimization. In-surance: Mathematics and Economics, 62, 5-15. https://doi.org/10.1016/j.insmatheco.2015.02.003
- 5. Hári, N., De Waegenaere, A., Melenberg, B. and Nijman, T.E. (2008) Estimating the Term Structure of Mortality. Insurance: Mathematics and Economics, 42, 492-504. https://doi.org/10.1016/j.insmatheco.2007.01.011
- 6. Lee, R.D. and Carte, L.R. (1992) Modeling and Forecasting U.S. Mortality. Journal of the American Statistical Association, 87, 659-671. https://doi.org/10.1080/01621459.1992.10475265
- 7. Cox, J.C., Ingersoll, J.E. and Ross, S.A. (1985) A Theory of the Term Structure of Interest Rates. Econometrica, 53, 385-407. https://doi.org/10.2307/1911242
- 8. Boyle, P.P. and Schwartz, E.S. (1977) Equilibrium Prices of Guarantees under Equity-Linked Contracts. Journal of Risk and Insurance, 44, 639-660. https://doi.org/10.2307/251725
