Advances in Applied Mathematics
Vol.
12
No.
03
(
2023
), Article ID:
63079
,
12
pages
10.12677/AAM.2023.123121
基于VMD-Self Attention-LSTM的短期电力 负荷预测
朵俞霖*,吕卫东#,李淑婷
兰州交通大学数理学院,甘肃 兰州
收稿日期:2023年2月21日;录用日期:2023年3月20日;发布日期:2023年3月27日

摘要
针对传统神经网络对长期时序特征提取能力较低,在电力负荷预测中精确度不高,提出一种VMD-Self Attention-LSTM混合预测方法,首先通过变分模态分解将负荷序列分解多个模态分量,以降低负荷序列的非平稳性和强非线性;其次,利用注意力机制模块改进长短期记忆网络,提取高维重构权重特征,获得负荷序列长期依赖关系;最后,将变分模态分解和改进长短期记忆网络结合用于电力负荷预测;此外,选择ANN和VMD-LSTM模型为对照组,针对混合模型的精度进行对比,经验证,VMD-Self Attention-LSTM混合模型的均方误差较其他方法有所下降,在对验证集的未来七日预测验证中,其平均绝对误差较ANN、VMD-LSTM模型分别下降3.49%、1.25%,该模型的预测性能更优异。
关键词
电力负荷预测,自注意力机制,VMD,LSTM

Short Term Power Load Forecasting Based on VMD Self Attention-LSTM
Yulin Duo*, Weidong Lv#, Shuting Li
School of Mathematics and Physics, Lanzhou Jiaotong University, Lanzhou Gansu
Received: Feb. 21st, 2023; accepted: Mar. 20th, 2023; published: Mar. 27th, 2023

ABSTRACT
The traditional neural network has low ability to extract long-term time series features and low accuracy in power load forecasting. Therefore, a VMD-Self Attention-LSTM hybrid forecasting method is proposed. Firstly, the load series is decomposed into multiple modal components through variational modal decomposition to reduce the non-stationary and strong nonlinearity of the load series; Secondly, the attention mechanism module is used to improve the short-term and short-term memory network, extract the high-dimensional reconstruction weight feature, and obtain the long-term dependence of load series; Finally, the combination of variational mode decomposition and improved short-term and short-term memory network is applied to power load forecasting; In addition, the ANN and VMD-LSTM methods were used as the control group to compare the accuracy of the mixed model. It was verified that the mean square error of the VMD-Self Attention-LSTM mixed model was lower than that of other methods. In the next seven days’ prediction verification of the validation set, its average absolute error was 3.49% and 1.25% lower than that of the ANN and VMD-LSTM models, respectively, and the prediction performance of the model was better.
Keywords:Electrical Load Forecasting, Self Attention, VMD, LSTM

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着我国经济实力的持续增长,居民用电、产业耗能的不断增加,我国电网的电力负荷也随之迅速增长。由于不同地区的发电量与用电量不相匹配,全国范围的电网调度具有深远意义,电力负荷预测成为电力系统中的重要环节,并且电力负荷预测是电网调度重要理论依据,对维持整个电力系统的稳定与社会平稳运行发挥着重要作用。电力负荷研究有利于制定最经济合理的系统发电计划,提高电力系统的经济效益和社会效益 [1]。因此,电力负荷预测受到了许多研究人员的关注。
目前的短期电力负荷预测大致分为传统预测方法与智能预测方法,传统预测方法如多元回归预测、时间序列预测等其原理简单,但随着电力系统智能化,影响电力负荷的因素趋于复杂化,监测数据趋于精细化,所以传统的预测方法已经不适应现阶段社会的发展。后来随着机器学习走入人们的视野,人们将机器学习方法运用于电力负荷预测中。这种基于机器学习的智能预测方法在当前数据化的电力系统中产生了很好的效果。蔡勇将SVM引入短期负荷预测中,并将气候因素与负荷同时作为训练样本的构成因子,取得了很好的预测结果 [2],但由于SVM在大规模样本训练中耗费时间长,该方法不常适用于高维数据。赵铭扬分别基于BP神经网络和Elman神经网络建立短期负荷预测的数学模型进行分析,通过预测误差及预测精度的对比得出结论,Elman神经网络模型的预测效果优于BP神经网络模型 [3],但是Elman神经网络模型只能提取局部序列的内在关联信息。李辉等人将循环神经网络对短期电力负荷进行预测,并通过粒子群算法对权值参数进行寻优 [4]。但循环神经网络很难建立长时间间隔状态之间的依赖关系。Kong等人基于LSTM模型对电力负荷进行预测 [5]。虽然LSTM模型通过引入遗忘门、更新门、输入门一定程度上解决了循环神经网络中的由于梯度消失带来的长短期依赖问题,但当历史负荷数据较长时,对长期历史信息的遗忘问题依然存在。同时,负荷数据通常为非平稳的时间序列,其噪声对电力负荷预测有很大的影响。徐岩等人利用经验模态分解方法对电力负荷数据进行预测 [6]。该方法分解得到的低频分量会出现模态混叠,不能突出低频分量的电力波动趋势。黄志祥等人利用变分模态分解方法将电力负荷分解为本征函数进行预测 [7] ;该方法能够自适应匹配每个模态的中心频率,有效的解决了模态混叠现象。2017年Google提出Transformer模型 [8],现如今广泛应用于自然语言处理,图像处理中。Transformer模型的核心就是Self Attention机制,它通过权值更新对史信息添加注意力参数,能够保留序列的长期历史信息。基于现有模型无法充分提取序列数据的长期依赖关系以及克服负荷序列的非平稳性与强非线性的问题,本文提出VMD-Self Attention-LSTM混合算法对电力负荷进行预测。
电力负荷预测是智能电网生效的关键节点,通过传入中控系统的电力负荷预测结果,指导并生成下一阶段的发电计划或电力调度计划。而电力负荷数据的非平稳性、非线性性以及历史信息提取不充分会导致预测误差较大,随着用电环境复杂化,对预测精度的要求也更高,针对上述问题,为保障电力系统的稳定运行,本文采用VMD方法降低负荷序列的复杂性和强非线性,并引入自注意力机制对LSTM网络进行改进,从高维特征中充分挖掘长期历史信息,所以本模型既能获得高维特征与负荷序列的时序相关性,又能拟合高维特征与负荷序列的回归特性。
2. 模型与方法
2.1. VMD分解原理
变分模态分解(VMD)是一种自适应、完全非递归的模态变分和信号处理的方法,通过将非平稳信号进行频域分析,把复杂信号分解为多个谐波信号。变分模态分解的整体框架是变分问题,使得每个模态的估计带宽之和最小,其中假设每个模态是具有不同中心频率的有限带宽 [9]。为解决变分问题,采用了交替方向乘子法,不断更新各模态及其中心频率,逐步将各模态解调到相应的基频带,最终各个模态相应的中心频率被一同提取出来 [10]。
假设将原始序列 分解为k个分量 ,每个本征函数(IMF)的中心频率为 ,约束条件为所有模态之和与原始信号相等,具体构造模型如下:
1) 步骤1,通过希尔伯特变换得到 的单边谱,与算子 相乘,将 的中心带调至相应的基带。
(1)
2) 步骤2,计算解调梯度的范数,并估计每个分量的带宽。
(2)
(3)
其中: 为狄拉克分布, 为分解后的模态分量, 为各模态对应的中心频率,“ ”为卷积符号, 为原始序列。
3) 步骤3,引入拉格朗日乘子 和二阶惩罚因子 。
(4)
4) 步骤4,利用交替方向乘子法(AMMD)更新各分量与中心频率,得到无约束变分模型的鞍点为模态分解的最优解,分量表示为:
(5)
其中: 表示频率, 、 、 分别为对应函数的傅里叶变换。
5) 步骤5,直到满足迭代停止条件,式(5)得到的k个分量为变分模态分解结果。
(6)
其中: 为第n次迭代分量, 为第 次迭代分量, 为误差。
2.2. 长短期记忆网络(LSTM)
LSTM是由循环神经网络(Recurrent Neural Network, RNN)改进的时间循环神经网络,RNN具有循环网络结构,能够处理需要记忆(历史数据的影响)的时间序列数据 [11]。由于RNN将神经网络上一层的隐藏层输出与当前时刻的输入同时作为当前层的输出,对于序列数据的预测有较大的优势,但在多次的循环中存在梯度消失和梯度爆炸问题。其后,长短期记忆网络随之出现,它通过输入门、遗忘门、输出门三个特殊的门控单元结构,在一定程度上解决了序列的长期依赖关系。LSTM在控制信息的累积速度时,同时也对新加入信息进行选择过滤,并有选择地遗忘前期累积的信息,由此改善循环神经网络的问题。因此,在输入序列数据时,都能对内部状态进行不断的更新,从而一直能够输出有价值的信息 [12]。LSTM给神经网络加上长期记忆功能,让信息不再衰减,其已凭借自身的巨大优势在自然语言处理以及数据挖掘领域取得了巨大的成功 [13]。
输入门:控制当前信息的重要程度并保留在细胞状态中,由sigmoid层和tanh层组成。
(7)
(8)
其中: 为sigmoid函数,tanh为双曲正切函数, 和 为权重系数, 为上一期输出值, 为当前时刻输入值, 和 为常数项。
遗忘门:当输入新信息时,前向传播更新历史信息参数,通过遗忘门来控制历史信息的重要程度。
(9)
其中: 为sigmoid函数, 为权重系数, 为上一时刻输出值, 为当前时刻输入值, 为常数项。
新细胞状态:通过输入门保留的当前信息与遗忘门保留的历时信息对细胞状态进行更新。
(10)
其中: 为当前时刻遗忘状态信息, 为当前时刻细胞状态信息, 为当前时刻输入状态信息, 为当前时刻保留输入状态信息。
输出门:输出值会基于当前细胞状态、该时刻的输入、前一时刻的历史输出完成一次过滤操作,做种决定当前时刻的输出值。
(11)
(12)
其中: 为sigmoid函数, 为权重系数, 为上一时刻输出值, 为当前时刻输入值, 为常数项。
长短期记忆网络结构如图1所示,它由于胞状态传播和学习权值控制长期依赖程度的特点,广泛应用于自然语言处理等序列数据模型。
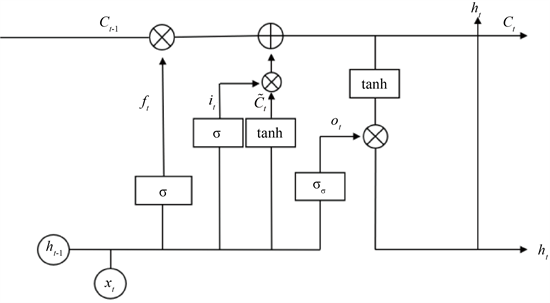
Figure 1. Schematic diagram of LSTM network structure
图1. LSTM网络结构示意图
2.3. Self Attention机制
在一个神经网络中,可学习参数越多,就表示模型的表达能力越突出,但当参数过多时,模型存储的信息量会爆炸式增长,这就带来了信息过载的问题,而我们往往希望得到快速而又精准的输出。在算力有限的情况下,我们需要将计算资源分配给较重要的学习任务,通过在网络中添加注意力机制,将关注重点聚焦于对当前学习任务更关键的信息上,降低其他信息的注意力或者过滤其他无关信息,这样就可以利用有限的资源实现对高价值信息的筛选,解决信息过载问题。其网络结构如图2所示,自注意力机制就是利用原始数据映射的query和key之间相似度的计算,通过可学习参数更新value,得到带有注意力机制的value值 [14] [15]。
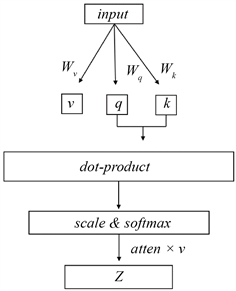
Figure 2. Self Attention mechanism network structure diagram
图2. 自注意力机制网络结构示意图
其中scale & softmax模块是对通过query与key学习得到的参数进行概率映射。
(13)
其中:S为query和key之间的余弦相似度,由两矩阵的点积表示, 为key的维度。
3. 组合模型改进
3.1. VMD-Self Attention-LSTM模型建立
电力负荷的影响因素是多方面的,其中历史负荷因素中蕴含着最重要的价值信息;其次与天气因素、温度、风速、电价、地理位置、日期等因素有着密不可分的关系。基于负荷预测的多维复杂特征,本文充分考虑影响电力负荷的复杂因素,融合序列分解算法、自注意力机制和LSTM模型,提出一种VMD-Self Attention-LSTM短期电力负荷预测方法,该方法将电力负荷数据分解为较平稳的子序列后,将多维特征时间序列传入自注意力机制模块,为每个输入特征提供对应的关注度,为充分提取长期依赖关系,将注意力权值矩阵输入LSTM模型得到预测结果。该方法流程如图3所示。

Figure 3. Schematic diagram of algorithm flow of hybrid model
图3. 混合模型算法流程示意图
将通过VMD分解的平稳子序列与其他特征合并为多为特征时间序列,克服负荷数据的非平稳趋势;在其后添加自注意力机制,时间步长序列能够从其本身学习关键信息并更新自身权值,从而获得多维时间序列的重要程度并提取序列间长期依赖关系,充分挖掘影响电力负荷的复杂特征;将更新注意力后的多维时间序列通过长短期记忆网络后由全连接层将输出映射到新的特征空间进行预测。且自注意力机制同时对高维数据参数学习中出现的梯度爆炸与梯度消失问题进行稀释。运用Self Attention与LSTM的改进算法是为了充分学习负荷序列的历史信息,把握影响未来时刻电力负荷的关键,使短期电力负荷预测更加精确。同时该模型很大程度上加深了序列数据的内在联系。
3.2. 评价标准
在层出不穷的模型中,人们通过对预测值与真实值之间的差距来衡量一个模型好坏 [16],在短期电力负荷预测中常用的损失函数有:
1) MSE (均方误差)
该损失函数最为常见,通过真实值与预测值之差的平方的期望值来评价模型好坏,均方误差越小,模型拟合效果越好。
(14)
2) MAPE (平均绝对百分比误差)
用预测值、真实值之差与真实值相比的绝对值来衡量模型的好坏,平均绝对百分比误差越小,模型拟合效果越好。
(15)
MSE避免了正负误差不能相加的问题,且由于对误差进行平方运算,加大了数值大的误差在指标中的作用,提高了灵敏度。MAPE以百分比表示,对预测的准确度表示更加直观,也可用于比较不同比例的预测。本文根据实际情况,选取MSE评价模型波动程度,选取MAPE作为评价模型的准确性的指标且最终结果保留在百分位。
4. 实例分析
本次实验平台采用Windows10下PyCharm Community Edition2021版本和Anaconda3开发环境,使用PyTorch开源框架搭建深度学习模型。
4.1. 模型数据来源和预处理
本文选取某地区11月1日~11月30日的实际电力负荷数据,采样间隔为15 min,并收集当地气象数据,日期数据。由于本文采集月度负荷数据,所以过滤了经济、季节等方面的因素。初始数据集中包含7维特征,其特征含义见表1,且以8:2的比例将数据集划分为训练数据集和测试数据集,同时我们对数据进行最大最小归一化,消除不同指标量纲和取值范围差异的影响,使数据落入[0, 1]区间范围内。
4.2. 序列分解
电力负荷数据具有波动性和周期性等时间序列特征,如图4所示,从图中可以发现,该序列有明显的周期性,为非平稳时间序列,利用该序列进行电力负荷数据的预测精确度不高,因此我们对其进行VMD分解。本文利用中心频率法确定分解模态数 ;惩罚因子 ;收敛误差 。图5为分解的序列图像,分解后各模态的本征函数如图6所示,从图中可以看到,IMF1本征函数的变化趋势与原序列大致相同,且其变化程度比较缓慢,IMF2本征函数变化也比较缓慢,剩余分量则为高频分量,变化较快。因此我们选择前四个分量作为负荷数据,对其进行深入分析。
Table 1. Indicators of influencing factors
表1. 影响因素指标

Figure 4. Time series of power load
图4. 电力负荷数据时间序列
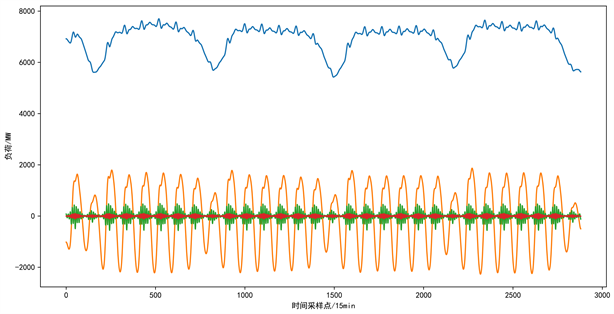
Figure 5. VMD decomposed sequence
图5. VMD分解后序列
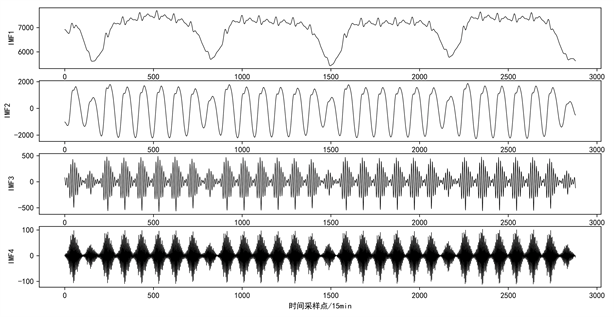
Figure 6. IMF function
图6. IMF函数
4.3. Self Attentiom-LSTM模型预测
我们将通过信号分解的原始负荷数据与其他影响因素整合后输入Self Attention-LSTM模型,对训练数据训练、更新参数后,在测试集数据中进行验证。
1) 建立数据的测试集与验证集,训练集用于完成参数更新,模型建立,验证集用于评价模型优劣程度。
2) 本文建立的LSTM模型网络结构见表2,隐藏层个数为2层,每层的节点数为20,输入维度为10,时间滑动步长为96,在隐藏层后添加线性层输出层,输出维度为1,作为预测结果,模型迭代200次。
完成迭代后输出预测结果与损失。图7为VMD-Self Attention-LSTM混合模型预测结果与真实值的对比图,从图中我们可以看到电力负荷变化呈现一定周期性,其变化规律随星期数呈现出周期趋势,且预测值与真实值之间的结果十分接近,但在一天中的用电高峰期与用电低峰期误差较大,其它时刻我们的混合模型在该数据集上有很好的效果。
4.4. 对照实验
为了验证VMD-Self Attention-LSTM混合模型是否具有实际意义,我们分别对该电力负荷数据进行ANN,VMD-LSTM预测,其中VMD-LSTM模型参数与VMD-Self Attention-LSTM混合模型参数一致,
Table 2. Self Attention LSTM model structure
表2. Self Attention-LSTM模型结构
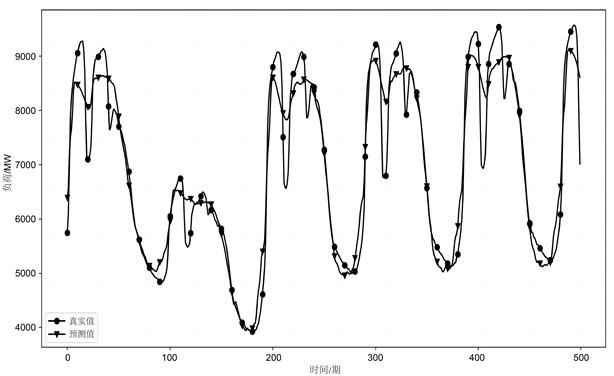
Figure 7. Power load forecasting
图7. 电力负荷预测
ANN模型设定两层隐藏层,各隐藏层节点数分别为64,128,激活函数为Relu函数。在实验过程中我们发现混合模型与LSTM模型中,增加神经元节点数、隐藏层个数对预测的准确度影响不大,而序列滑动窗口步长对序列的准确度影响较大。图8为不同模型预测值与真实值的对比图,各模型的评价指标对比结果见表3。

Figure 8. Prediction results of different models
图8. 不同模型预测结果
4.5. 结果分析
LSTM是本次仿真实验的基础模型,我们的混合模型是基于该模型进行改造的结果,通过VMD序列分解,我们得到了较平稳的分解序列,进而将频率较低的4个分解序列与气候因素,日期因素共同输入改进的Self Attention-LSTM模型进行预测,结合对真实值与预测值的图像输出。我们发现电力负荷成一定的周期规律,这与我们日常生活用电情况是相符合的。同时,本文从准确度和收敛速度两个角度衡量模型的预测水平。
准确度,为了更直观的看到模型的准确度,本文通过求得预测值与真实值的均方误差,该模型的在经过200次迭代后,其均方误差收敛在3800 MW左右,均方根误差为61.28 MW,说明模型具有较优异的预测性能。
收敛速度,由于本次实验数据量较小,其迭代速度较快,我们通过模型损失函数的收敛速度评价模型,从图中可以看出,该模型在经过50迭代后,损失函数趋于平缓。
本文对三种模型做出比较见表3,从收敛迭代和均方误差两方面来看,三个模型在收敛迭代中在50次后趋于平缓,但ANN模型均方误差最大;而我们的混合模型均方误差最小,在电力负荷预测的精确度上表现最优异。且MSE较其他模型分别下降了12.6%,2.80%。
Table 3. Comparison of different model
表3. 不同模型对比
为验证模型的有效性,我们基于训练模型对11月23日至11月30日全天的电力负荷进行预测,三种模型的预测精度见表4,其中ANN模型的平均预测精度为95.14%,VMD-LSTM模型的平均预测精度为97.38%,VMD-Self Attention-LSTM模型的平均预测精度为98.63%,最大误差为2.00%。结合如上结果,VMD-Self Attention-LSTM模型相比于ANN模型的预测精度提高了3.49%,相比于VMD-LSTM模型的预测精度提高了1.25%,因此,进行VMD分解后,减少序列本身非平稳因素,再加入自注意力机制后,对序列特征的赋予关注度,进一步提高了模型的预测精度。
Table 4. Comparison of load forecast errors
表4. 负荷预测误差对比
5. 结论
在智能电网快速发展的环境下,电力负荷预测质量的提高与电力系统的稳定运行联系密切。本文在长短期记忆网络的基础上,考虑电力负荷数据的非平稳性和长距离依赖关系,提出了一种VMD-Self Attention-LSTM混合模型,基于信号分解理论和自监督算法,首先利用变分模态分解技术获得电力负荷数据的模态分量,然后结合气象因素与日期因素构成多维特征时间序列,再将其传入自注意力机制模块,进而获得权重矩阵,最后根据LSTM网络进行训练和预测。由研究结果可知,针对复杂多变的电力负荷序列,采用变分模态分解模型将其分解成若干模态分量,其在采样和噪声方面有较好的鲁棒性,能够有效地降低负荷序列的非平稳性与强非线性,为后期打下良好基础;采用自注意力机制对多维特征时间序列添加权重,初步提取时间序列长距离依赖关系,促进LSTM网络对历史信息的充分提取,同时减少网络参数。因此,VMD-Self Attention-LSTM混合模型在短期电力负荷预测中具有一定的优势,为短期电力负荷预测提供了一种新方法。
基金项目
国家自然科学基金(11961039)。
文章引用
朵俞霖,吕卫东,李淑婷. 基于VMD-Self Attention-LSTM的短期电力负荷预测
Short Term Power Load Forecasting Based on VMD Self Attention-LSTM[J]. 应用数学进展, 2023, 12(03): 1195-1206. https://doi.org/10.12677/AAM.2023.123121
参考文献
- 1. 吴茜. 电力负荷预测方法综述[J]. 科技与企业, 2012(13): 359. https://doi.org/10.13751/j.cnki.kjyqy.2012.13.221
- 2. 蔡勇. 基于支持向量机的短期电力负荷预测研究[D]: [硕士学位论文]. 武汉: 华中科技大学, 2007.
- 3. 赵铭扬. 基于神经网络的短期电力负荷预测研究[D]: [硕士学位论文]. 银川: 宁夏大学, 2016.
- 4. 李辉, 王军. 基于粒子群算法与循环神经网络的短期电力负荷预测[J]. 软件导刊, 2017, 16(11): 125-128.
- 5. Kong, W., Dong, Z., Jia, Y., et al. (2019) Short-Term Residential Load Forecast-ing Based on LSTM Recurrent Neural Network. IEEE Transactions on Smart Grid, 10, 841-851. https://doi.org/10.1109/TSG.2017.2753802
- 6. 徐岩, 向益锋, 马天祥. 基于EMD-CNN-LSTM混合模型的短期电力负荷预测[J]. 华北电力大学学报(自然科学版), 2022, 49(2): 81-89.
- 7. 黄志祥, 周莉. 基于VMD-LSTM的短期电力负荷预测研究[J]. 洛阳理工学院学报(自然科学版), 2022, 32(3): 76-80+96.
- 8. Vaswani, A., Shazeer, N., Parmar, N., et al. (2017) Attention Is All You Need. Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, 4-9 December 2017, 6000-6010.
- 9. 吴龙文, 聂雨亭, 张宇鹏, 何胜阳, 赵雅琴. 基于变分模态分解的自适应滤波降噪方法[J]. 电子学报, 2021, 49(8): 1457-1465.
- 10. 刘长良, 武英杰, 甄成刚. 基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断[J]. 中国电机工程学报, 2015, 35(13): 3558-3565.
- 11. 王婷. 基于LSTM深度网络的电力负荷预测[D]: [硕士学位论文]. 太原: 山西大学, 2020. https://doi.org/10.27284/d.cnki.gsxiu.2020.000860
- 12. 高亚静, 孙永健. 基于新型人体舒适度的气象敏感负荷短期预测研究[J]. 中国电机工程学报, 2017, 37(7): 1946-1955.
- 13. 荆昱阳, 张利强. 基于Pytorch的长短期记忆网络实现及应用[J]. 制造业自动化, 2021, 43(12): 167-169+177.
- 14. 李浩君, 方璇, 戴海容. 基于自注意力机制和双向GRU神经网络的深度知识追踪优化模型[J]. 计算机应用研究, 2022, 39(3): 732-738. https://doi.org/10.19734/j.issn.1001-3695.2021.08.0345
- 15. 董家富, 万雄, 王岩, 叶瑞丽, 熊志杰, 范海威, 薛一波. 基于XGB-Transformer模型的短期电力负荷预测[J]. 电力信息与通信技术, 2023, 21(1): 9-18.
- 16. 吴瑞盈. 基于机器学习的短期电力负荷预测模型研究[D]: [硕士学位论文]. 重庆: 重庆理工大学, 2022. https://doi.org/10.27753/d.cnki.gcqgx.2022.000637
NOTES
*第一作者。
#通讯作者。
