Finance
Vol.
09
No.
04
(
2019
), Article ID:
31245
,
14
pages
10.12677/FIN.2019.94041
Research on Multi-Factor Stock Selection Model Based on EKPCA Algorithm
Yu Huang, Houqing Fang, Lingfei Dai, Tingting Chen
Faculty of Science, Jiangsu University, Zhenjiang Jiangsu

Received: Jun. 20th, 2019; accepted: Jul. 3rd, 2019; published: Jul. 12th, 2019

ABSTRACT
The multi-factor stock selection model is the mainstream method in quantitative investment. This paper introduces the Efficient Kernel Principal Component Analysis (EKPCA) algorithm for the first time. The high-efficiency kernel principal component is used as the independent variable to establish the regression equation to predict the rate of return and construct a multi-factor stock selection model. Based on the empirical analysis of the constituents of SSE 180, this paper selects more than 50 impact factors including fundamentals, technical indicators and investor sentiment indicators, and uses the EKPCA algorithm to determine the basic model and extracts high-efficiency kernel principal components in the high-dimensional feature space. Compared with the classical KPCA algorithm, the EKPCA algorithm has higher feature extraction efficiency. The backtest results show that the beta coefficient and Sharpe ratio of the constructed portfolio are better than the market benchmark level in the selected time period, which indicates that the model has a better stock picking effect.
Keywords:EKPCA Algorithm, Multi-Factor Stock Selection, The General Entropy, Feature Extraction, Kernel Function
基于EKPCA算法的多因子选股模型研究
黄钰,房厚庆,戴凌飞,陈婷婷
江苏大学理学院,江苏 镇江

收稿日期:2019年6月20日;录用日期:2019年7月3日;发布日期:2019年7月12日

摘 要
多因子选股模型是量化投资中的主流方法。本文首次引入高效的核主成分分析(Efficient Kernel Principal Component Analysis, EKPCA)算法,以高效的核主成分为自变量建立回归方程预测收益率,构建多因子选股模型。本文基于上证180的成分股进行实证分析,选取包含基本面、技术指标及投资者情绪指标等50多个影响因子,引用EKPCA算法确定基本模式,在高维特征空间提取高效核主成分。与经典KPCA算法对比,EKPCA算法具有更高的特征抽取效率。回测结果显示,构造的投资组合的贝塔系数和夏普比率在所选时间段内均优于市场基准水平,这表明该模型具有较好的选股效果。
关键词 :EKPCA算法,多因子选股,通用熵,特征提取,核函数

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
人工智能技术的高速发展,机器学习算法的持续改进,使得量化投资更具实用价值。1971年,美国巴克莱国际投资管理公司发行了世界上第一只指数基金,这标志着量化投资交易正式拉开帷幕。在美国,量化投资交易己有将近50年的历史,量化投资交易量从开始到现在己经占到美国金融市场交易量的30%以上。量化投资起源于美国,却在全球资本市场的浪潮中得到快速的发展。国外成熟金融市场的发展经验表明,利用量化投资可以有效提高金融交易市场的资金流动性。在2004年,国内首次出现量化基金——光大保德信量化核心基金,此后因为各种原因,发展比较缓慢。最主要的量化投资策略就是多因子策略、CTA策略和对冲策略。其中,多因子策略2007年在国内出现,此后一直占据量化投资策略的主导地位;CTA策略在2011年进入国内市场后,并没有较大发展空间,直到2015年才开始发展起来;对冲策略出现在2012年左右,主要依托股指期货的对冲效应 [1] 。量化投资减少了主观判断等因素的影响,比传统投资更具科学性,越来越受投资者的青睐。
国际上经典的选股模型是资本资产定价模型(CAPM)、套利定价理论模型(APT)、法玛和弗伦奇的三因子模型。当前,中国的股票市场对于多因子模型的研究还处在一个初级阶段,绝大多数的研究都局限于证券公司的专业研究部门,在学术界算是比较新兴的领域。
国内学者通过借鉴国外先进的量化模型,构建了不同类型的量化选股模型。范烨 [2] 构建了多因子模型进行选股研究,对多因子进行排序打分,并且确定相关阈值对因子进行筛选;李娜 [3] 等提出基于k-means聚类的选股模型,该模型利用数据的自动学习来对数据进行特征分类选取因子;苏治 [4] 构建了基于核主成分遗传算法改进的支持向量回归机人工智能选股模型,提高了传统模型的预测精度;贾秀娟 [5] 使用随机森林处理变量,提出基于随机森林的支持向量机模型进行选股研究,提高了模型的识别精度。其中,多因子选股模型有两种判别方法,一种是打分法 [2] [6] ,另一种是回归法 [7] 。与打分法相比,回归法可以根据股票市场上的突发情况,能够及时地调整模型对各个因子的敏感度,而且简单、快速,更便于程序化交易。因此,本文采用回归法对多因子模型进行实证研究。
我国股票市场存在T + 1制度,缺乏有效的做空机制和金融衍生工具,这些都限制了量化投资在中国市场的发展。我国A股市场发展还不完善,风格多变,多处于弱有效状态,因子之间关系复杂,内在混乱,各个财务指标之间的线性关系不明显,这里利用普通的线性降维效果并不理想。为了探究适应我国A股市场的量化投资策略,本文提出高效的核主成分分析方法,在高维空间中提取主要的非线性特征。经典KPCA方法常用于特征提取、图像识别、人脸识别等 [8] 。KPCA作为抽取复杂数据特征的一种非线性方法,当训练样本的规模很大时,它的抽取效率并不高,因此本文提出一种新型EKPCA算法来提高特征抽取效率。EKPCA算法的基本思想是剔除对特征抽取贡献小的训练样本,确定贡献大的训练样本,即确定基本模式,运用特征相关分析来逐个确定基本模式,基本模式的个数可由用户根据需要自己设置。再用已确定的基本模式重新建立KPCA模型,在高维空间进行特征抽取,将抽取的主成分进行收益率回归。本文首次将该算法应用到多因子选股模型中,为量化投资策略提供新的研究思路。
2. 影响因子选取
本文选取的因子包括上市公司的基本面数据,技术指标数据及投资者情绪指标数据 [9] 等50多个因子。表1给出了所选因子:
Table 1. Selected impact factors
表1. 选取的影响因子
3. 多重共线性检验
本文选取的影响因子比较多,因子之间可能存在较高的相关性,这会严重影响选股模型的准确性,使得之后的回归预测失效。因此,本文引用方差膨胀因子(VIF)检验法 [10] ,影响因子 的方差膨胀因子记为VIF,它的计算方法为:
式中, 是以 为因变量时对其它影响因子 , 回归的模型拟合优度。如果最大的VIF超过10,常常表示多重相关性将严重影响回归参数的估计值。基于我国股票市场弱有效且经济因素复杂的背景下,多维度的因子之间不存在明显的线性相关关系。因此,本文引用EKPCA算法进行非线性降维解决上述问题。
4. 基于EKPCA算法的多因子选股模型建立
4.1. EKPCA算法的基本原理
经典KPCA是传统PCA的一种非线性拓展,其目的是从数据中抽取最具表现力的特征 [11] 。因子之间存在非线性相关关系,不能直接用PCA进行降维,而KPCA的基本思想是将原始训练样本通过一个合适的非线性隐函数 映射到高维特征空间中,原空间中非线性可分变量很大程度可以转化为高维特征空间中的线性可分变量,然后在高维空间中运行PCA,从而抽取数据的特征。通过研究映射到高维空间中的点的几何性质,我们知道点之间的距离和夹角都可以用核函数 来表示,不需要知道 的具体形式。常用的核函数有线性核、多项式核、高斯核、拉普拉斯核、Sigmoid核等,本文根据模型需要主要引入表2中的两种核函数:
Table 2. Common kernel functions
表2. 常见的核函数
其中, , 为原始输入空间的训练样本。利用核函数建立核矩阵K,核矩阵K其实是内积矩阵,且一定是半正定矩阵 [12] ,其中
(1)
式中, , 为训练样本,N为训练样本的个数。
由上述表达式可知核矩阵的规模与训练样本的个数成正比,则KPCA的计算效率与训练样本的个数成反比,多因子选股模型一般选取的股票数量都较多,KPCA抽取效率较低。近年来,很多算法被提出用来提高KPCA的计算效率 [13] 。本文引用其中一种特征抽取效果较好的EKPCA算法,该算法可以用小部分训练集(基本模式)的线性组合来近似表达KPCA的特征抽取效果。对全体训练样本进行特征抽取时,每个特征分量其实就是一系列核函数的线性组合,训练样本越多,特征抽取效率越低。同时,在特征抽取过程中,有些训练样本对特征抽取的贡献非常小。EKPCA算法的基本思想是在进行特征抽取前,先剔除对特征抽取贡献小的训练样本,保留贡献大的训练样本,保留下来的训练样本即基本模式,这里运用特征相关分析来逐个确定基本模式,基本模式的个数由用户自己设置。再重新构建KPCA模型。
EKPCA算法与KPCA算法相比主要有两个优点:第一,基本模式的个数一般远远小于全体训练样本的个数,这使得EKPCA算法比KPCA算法的抽取效率高;第二,在特征抽取时,KPCA需要对 (N是全体训练样本的个数)的核矩阵进行特征分解,而EKPCA只需要对 (s是基本模式的个数)的核矩阵进行特征分解,这说明EKPCA比KPCA需要更少的存储空间 [14] 。
4.2. 核函数参数选择
首先,对训练样本进行z-score标准化处理,即使处理后的数据均值为0,标准差为1。
其次,引入最大通用熵来确定多项式核函数的参数c和d以及高斯核函数的参数 。主要步骤如下:
步骤1:定义特征空间中点之间的余弦距离
(2)
将(1)式带入(2)式得到下式
(3)
由上述表达式可知,如果引用高斯核函数,则
(4)
同样,如果引用多项式核函数或其他的核函数,则特征空间中每个样本向量的长度标准化为1,也可以得到 。那么,核矩阵在某种程度上是特征空间中余弦矩阵的一种特殊形式,因此,理论上可以用余弦矩阵来学习核矩阵及其参数 [8] 。如果 ,则特征空间中的向量很可能相互正交,它们的类间散度和类内散度都很大 [12] ,该情形下,很难正确分开样本数据。如果 ,则特征空间中的所有样本向量将会集中于一点,或者位于同一直线上,显然该情形也不利于样本分类。
步骤2:定义通用熵如下:
(5)
将(4)式代入(5)式得到:
(6)
根据前面提到的两种情况 和 ,通用熵 将会取到最小值0,这将妨碍样本的分类。因此本文选取通用熵的最大值对应的参数建立核函数,便于对数据进行分类。这就是一个凸优化问题:
或
4.3. 确定基本模式
有两种常见的确定基本模式的方法,一种是前向选择算法,另一种是后向选择算法 [11] 。考虑时间复杂度,本文选用前向选择算法,耗时较小。特征抽取的一项基本原则是,由不同投影方向得到的特征之间应尽量互不相关,因此,确定基本模式的要求是由两个基本模式得到的特征集之间具有较小的特征相关,这样特征抽取结果的贡献率比较大,综合信息的能力较强。利用核矩阵列向量 之间的特征相关即核矩阵列向量之间的余弦距离,来确定基本模式。两个核矩阵列向量 和 之间的余弦距离为
确定基本模式的过程如下:
步骤1:确定前两个基本模式。
找出两个核矩阵的列向量 和 满足
(7)
然后,将它们对应的原始训练样本 和 作为前两个基本模式,重新标记为 和 ,将它放入新的集合A中, ,构成新的矩阵 。
步骤t:确定第t个基本模式 。
假设已经在前面 步中,确定了基本模式 ,并且 ,由这些基本模式构成了下面的新矩阵:
对于任意 ,设候选的核矩阵列向量是 ,
定义候选向量 与矩阵 之间的余弦距离为
(8)
式中,
是
的第q列向量:
。利用式(7)确定
的最小值,与最小值对应的原始训练样本就确定为第t个基本模式,记为
,将它加入到集合 中。将样本
对应的核矩阵列向量加到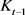 作为该矩阵的最后一列,变为新矩阵
。
作为该矩阵的最后一列,变为新矩阵
。
重复上述过程直到 ,就确定了所有的基本模式 以及新的矩阵 。
4.4. 重建KPCA模型
将训练样本 映射到高维之后,对映射后的数据 进行中心化处理,即均值满足
我们知道将一个向量 在v方向上的投影,若投影方向的模长 ,则投影后的向量为 。这就意味着在单位向量上投影后的坐标为 。那么特征抽取要求投影之后的数据尽可能互不相关,即要求找到一个投影方向v,使得投影后的数据方差最大。投影后的方差为
(9)
上式中,假设所有样本已经经过中心化处理, 为投影点的均值, 为原训练样本的协方差矩阵则找出最优投影方向的问题可转化为下面的优化问题:
(10)
为解决该问题,引入拉格朗日乘子 ,建立拉格朗日函数
(11)
令 对v和 的偏导数为零得
(12)
(13)
将(12)式和(13)式代入(10)式可转为
(14)
那么求解该优化问题可转化为求解协方差矩阵C的最大特征值。因此,对高维特征空间进行特征抽取时可转化为求解高维空间的协方差矩阵D (D为原始训练样本映射到高维空间后的协方差矩阵)的前p (p为主成分的个数)个最大特征值。高维特征空间的协方差为:

对D进行特征分解的特征方程为
(15)
式中, 为该特征方程非负特征值对应的特征向量。
由于直接对该协方差矩阵进行特征分解无法得到具体特征值,可以转化为对已确定的基本模式构建的核矩阵 进行特征分解得到特征值。其中,
(16)
令 (17)
令 (18)
令 (19)
其中, 。
将(17)式代入特征方程(15)可以得到:
(20)
将上述等式两边同时左乘 ,右乘 ,得:
(21)
其中, 为新特征方程(21)式的特征向量。
将(18)式和(19)式代入(21)式,得:
(22)
求解方程(22)得到前p个最大特征值 以及其对应的特征向量 。因此,原始训练样本的映射在高维空间特征向量上的投影(即主成分)可以如下表示:
(23)
其中, 是向量 的第i个分量 [11] ,s为已确定的基本模式的个数。
4.5. 多元线性回归预测
在高维特征空间中抽取了样本的p个主成分,对这p个主成分建立多元线性回归模型,如下:
(24)
其中,y是股票收益率, 为回归系数, 为主成分矩阵B的第k个分量, 为残差矩阵。利用最小二乘法进行回归参数估计,得到
(25)
再将上式结果进行因变量y的预测为
利用方差分析法中的F统计量的P值(即显著性值)对回归方程进行显著性检验,一般P值小于0.05表示回归方程具有统计学意义。
5. 实证分析及实验结果
本文选用上证180成分股作为研究对象,选用前文所述的50多个因子进行基于EKPCA算法的多因子选股模型实证分析。其中,基本面数据选取上市公司2013至2018年这六年财务报表的季度数据,技术指标数据选取2013至2018年的周行情数据。这些数据时间跨度大,范围广,层面宽,获取数据样本充足,构建的投资组合考虑方面越周到,数据获取遵循可靠性,实效性,全面性,精确性,可操作性等原则。数据来源为东方财富网站Choice金融终端,该数据库较权威,数据采集质量高,实验结果可信度高。当某只股票的指标数据空缺较多时,认为该样本不具备研究价值并且直接剔除,对于其它空缺值,本文通过MATLAB2016a软件进行数据预处理。由于因子之间的量纲不同,需要先将这50多个因子标准化之后,再通过SPSS 22.0统计软件进行多重共线性检验,下表3为输出的结果:
Table 3. Collinearity test
表3. 共线性检验
由表3可见,最大方差膨胀因子为238.606远远大于10,认为这些因子之间的多重共线性比较严重,不能真实反映股票的收益率走向。因此,利用EKPCA算法模型进行降维处理,首先,找到最大通用熵对应的多项式核参数c和d分别是1和4,高斯核参数 为8.2;然后,吴世农 [15] 等采用非回置式随机抽样方式确定上海股市适度的组合规模为21~30种股票,这一适度的组合规模可以较好地减少总风险,根据这一理论确定基本模式为30只股;最后,将这30只股票映射到高维空间进行特征抽取,对比两种核函数的特征抽取效率,发现多项式核函数只需抽取4个高效核主成分即可达到95%的方差贡献率,而高斯核函数需要抽取21个高效核主成分才能达到同样的效果,因此,本文采用多项式核函数建立核函数进行特征抽取。经过MATLAB 2016a程序输出结果如下:

Figure 1. Variance contribution histogram and cumulative contribution histogram
图1. 方差贡献率直方图与累计贡献率折线图

Figure 2. Eigenvalue lithotripsy
图2. 特征值碎石图
由图1和图2可知选取前4个最大的特征值,它们的累计方差贡献率可以达到95%,具有较强的综合因子差异的能力。再对比EKPCA算法与KPCA算法的特征抽取时间,发现KPCA算法完成特征抽取平均需要0.1158秒,而EKPCA算法平均只需0.0154秒,这表明EKPCA算法确实提高了特征抽取效率。
将确定的30个基本模式对应的收益率与抽取的4个高效核主成分进行以收益率为因变量,高效核主成分为自变量的多元线性回归分析,预测基本模式的收益率。收益率的计算公式为
其中, 为当期收盘价, 为前期收盘价,本文使用月收益率效果更好。通过SPSS 22.0输出回归结果如表4所示:
Table 4. Parameter estimation of multiple linear regression
表4. 多元线性回归的参数估计
根据方差分析表中F检验对应的P值(显著性)为0.012 < 0.05,说明至少有一个自变量能够有效预测因变量,回归模型具有实际应用价值。
再根据吴世农 [14] 等人的理论,本文选用收益率最高的前25只股票进行等权重分配的投资组合。投资组合结果如表5所示:
Table 5. Investment portfolio
表5. 投资组合
6. 模型评价
好的投资组合具有高收益低风险的特征,因此,对已确定的组合投资进行绩效评价涉及对超额收益率以及风险的检测。本文将2018年底所有上证180的股票数据代入模型进行回测检验,收益率采用周行情数据,由MATLAB 2016a输出的图3及结果,发现上证180在该时间段中的平均收益率为1.19%,而本模型确定的投资组合的平均收益率达到1.75%,说明构造的该投资组合的收益情况较好。再用 系数和夏普比率对组合的风险进行评价, 系数用来衡量投资组合相对于整个股市的价格波动情况,其值越大说明风险越大。夏普比率可以同时对收益以及风险加以综合的指标,其值越大,说明投资组合单位风险所获的风险回报越高。经过计算,投资组合的评价情况如表6所示。
由表6数据可以得出,该投资组合在所选时间段内系统风险小于大盘,且收益绩效大幅度超过大盘,可以获得较高的超额回报。

Figure 3. Portfolio performance analysis
图3. 投资组合绩效分析
Table 6. Portfolio risk return situation
表6. 投资组合风险收益情况
7. 总结
本文主要研究了基于EKPCA算法的多因子量化选股模型,该模型通过特征相关即核矩阵列向量之间的余弦距离来确定基本模式,不仅提高了以往学者的KPCA算法的特征抽取效率,而且减少了存储空间。从识别角度来看,EKPCA的识别效果也是很好的,可以在训练样本规模较大时,高效地找出影响股票收益率显著因子,构造较好的投资组合。本文在研究多因子相关关系时,通过方差膨胀因子检验法检测发现所选多因子间存在严重的多重共线性问题,提出EKPCA算法进行降维。舍弃最小特征值对应的特征向量,仍然能够保持原样本低维结构的完整性,不仅使样本的采样密度增大,而且起到降噪的效果。
基金项目
江苏大学2019年大学生实践创新训练计划项目(项目编号:5553170019)。
文章引用
黄 钰,房厚庆,戴凌飞,陈婷婷. 基于EKPCA算法的多因子选股模型研究
Research on Multi-Factor Stock Selection Model Based on EKPCA Algorithm[J]. 金融, 2019, 09(04): 327-340. https://doi.org/10.12677/FIN.2019.94041
参考文献
- 1. 王春丽, 刘光, 王齐. 多因子量化选股模型与择时策略[J]. 东北财经大学学报, 2018, 119(5): 83-89.
- 2. 范烨. 多因子选股模型建立的研究[J]. 全国流通经济, 2018(3): 64-65.
- 3. 李娜, 毛国君, 邓康立. 基于k-means聚类的股票KDJ类指标综合分析方法[J]. 计算机与现代化, 2018, 278(10): 12-17.
- 4. 苏治, 傅晓媛. 核主成分遗传算法与SVR选股模型改进[J]. 统计研究, 2013, 30(5): 54-62.
- 5. 贾秀娟. 基于随机森林的支持向量机量化选股[J]. 区域金融研究, 2019(1): 27-30.
- 6. 吕凯晨, 闫宏飞, 陈翀. 基于沪深300成分股的量化投资策略研究[J]. 广西师范大学学报(自然科学版), 2019, 37(1): 1-12.
- 7. 徐景昭. 基于多因子模型的量化选股分析[J]. 金融理论探索, 2017(3): 30-38.
- 8. 朱晨曦. 我国A股市场多因子量化选股模型实证分析[D]: [硕士学位论文]. 北京: 首都经济贸易大学, 2017.
- 9. 凌士勤, 苏乐. 投资者情绪与股票收益的实证研究——基于扩展卡尔曼滤波的方法[J]. 时代金融, 2017(6): 192.
- 10. 王锐. 岭回归分析在解决经济数据共线性问题中的应用[J]. 经济研究导刊, 2018(22): 144-147.
- 11. Fan, Z., Wang, J., Xu, B. and Tang, P. (2014) An Efficient KPCA Algorithm Based on Feature Correla-tion Evaluation. Neural Computing and Applications, 24, 1795-1806. https://doi.org/10.1007/s00521-013-1424-9
- 12. 周志华. 机器学习[M]. 北京: 清华大学出版社, 2016: 60-62, 128.
- 13. Sun, R., Tsung, F. and Qu, L. (2007) Evolving Kernel Principal Component Analysis for Fault Diagnosis. Computers & Industrial Engineering, 53, 361-371. https://doi.org/10.1016/j.cie.2007.06.029
- 14. 范自柱. 新型特征抽取算法研究[M]. 合肥: 中国科学技术大学出版社, 2016: 95-102, 122-128.
- 15. 吴世农, 韦绍永. 上海股市投资组合规模和风险关系的实证研究[J]. 经济研究, 1998(4): 22-29.
