Advances in Education
Vol.
09
No.
03
(
2019
), Article ID:
30038
,
8
pages
10.12677/AE.2019.93037
Using Numerical Methods and Tools to Deepen the Teaching Content of “Fluid Mechanics” Course
Zhimin Lin*, Yongheng Zhang, Liangbi Wang
School of Mechanical Engineering, Lanzhou Jiaotong University, Lanzhou Gansu

Received: Apr. 10th, 2019; accepted: Apr. 23rd, 2019; published: Apr. 30th, 2019

ABSTRACT
The engineering education certification standard clearly states that the goal of personnel training should enable students to have the ability to solve complex engineering problems. Thus, it is necessary to add examples having the features of complex engineering problems continuously in the basic major courses and major courses in teaching. “Fluid Mechanics” course takes an extremely important position in the personnel training process of relevant undergraduate majors. Exploring and solving the complex engineering problems play an important role in cultivating students’ ability of analyzing, solving problems and acquiring the needed knowledge and tools to solve the complex engineering problems. This paper takes the pipeline water hammer phenomenon as an example to illustrate the process of analyzing, modeling and solving the problem. It provides a reference for deepening the teaching content of the course of Fluid Mechanics and accumulating cases for solving complex engineering problems.
Keywords:Fluid Dynamics, Curriculum Construction, Numerical Methods, MATLAB
运用数值计算方法和工具深化《流体力学》 课程教学内容
林志敏*,张永恒,王良璧
兰州交通大学机电工程学院,甘肃 兰州

收稿日期:2019年4月10日;录用日期:2019年4月23日;发布日期:2019年4月30日

摘 要
工程教育专业认证标准明确要求人才培养目标要使学生具备解决复杂工程问题的能力。为此,应在相关专业基础课及专业课等教学环节中不断引入带有工程复杂问题特征的案例。《流体力学》课程在相关本科专业的人才培养过程中占有极其重要的地位,从中挖掘带有复杂工程问题特征的案例进行分析和求解,对于培养学生分析和解决问题的能力,获取和掌握解决复杂工程问题所需知识和工具具有重要作用。本文在分析《流体力学》课程体系的基础上,以管路水击现象为例,说明了问题的分析、建模和求解过程,为深化《流体力学》课程教学内容,积累求解复杂工程问题案例提供了参考。
关键词 :流体力学,课程建设,数值计算方法,MATLAB

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
2016年,我国正式加入国际工程教育《华盛顿协议》组织,截至2017年底,全国共有198所高校的846个工科专业通过工程教育专业认证。目前,我国工程教育专业认证已覆盖21个专业类,计划2020年实现所有专业大类全覆盖 [1] 。《工程教育认证标准》包括通用标准和补充标准,支撑毕业要求的课程体系由各学校根据自身办学定位、人才培养目标和办学特色自主设置,但针对专业大类的补充标准对数学与自然科学类课程、工程基础类课程、专业基础类课程与专业类课程、工程实践与毕业设计(论文)和人文社会科学类通识教育课程涉及的知识领域做了具体的规定 [2] [3] 。《工程教育认证标准》制定的毕业要求有12项,其中很多项要求学生通过专业培养和训练能够针对复杂工程问题进行分析、研究、提出解决方案、运用数学、自然科学、工程基础和专业知识、使用现代工具解决复杂工程问题。《工程教育认证标准》还对“复杂工程问题”的特征进行了说明 [2] [4] 。虽然复杂工程问题具有综合性、多目标性等特征,但复杂的问题可进行分解,运用相关学科的知识进行解决和综合 [5] 。
复杂工程问题在课程设计、综合实验、毕业设计(论文)中能够较好地体现。而在相关工程基础类课程、专业基础类课程中挖掘带有复杂工程问题特征的案例进行分析和求解,对于培养学生分析、解决复杂工程问题的能力,获取和掌握解决复杂工程问题所需知识和工具具有重要作用。《流体力学》课程是能源动力类专业的主干、核心专业基础类课程,也是其他许多工学类专业重要的工程基础类或专业基础类课程,该门课程与工程实际问题密切相关,是学习相关专业课程和专业发展不可缺少的技术基础理论 [3] [6] [7] 。本文在分析《流体力学》课程体系的基础上,以管路水击现象为例,说明问题的分析、建模和求解过程,为深化《流体力学》课程教学内容,积累求解复杂工程问题案例提供参考。
2.《流体力学》课程体系分析
2017年根据《工程教育认证标准》我校修订了能源与动力工程专业人才培养计划,能源与动力工程专业《流体力学》课程安排在第4学期,共计64学时,其中课堂讲授60学时,实验4学时。对照毕业要求,《流体力学》课程支撑毕业要求的第1项和第4项,具体指标点为:通过本课程的学习使学生具备解决能源与动力工程中复杂工程问题所需的宽厚、扎实的动力工程及工程热物理学科基础知识;能够利用基础科学和专业技术对内燃机、热力发电厂动力装置涉及的复杂工程问题进行探索和研究。
根据人才培养计划,对《流体力学》的教学大纲课程进行了修订。目前采用孔珑主编的工程流体力学(第四版) [8] 作为授课教材。虽然面向能源动力类专业的教材章节安排上有所不同,但基本内容基本一致 [8] [9] [10] 。以孔珑主编的《工程流体力学(第四版)》为例,基本内容包括:流体及其物理性质,流体静力学,流体运动学,积分形式的流体动力学分析,相似原理和量纲分析,管内流动和水力计算,理想流体的有旋和无旋流动,黏性流体微分形式的流体动力学分析,气体的一维流动,气体的二维流动。流体力学教学内容中关于流动现象的描述有些可通过日常生活观察或通过实验能较为直观地观测到,如层流、紊流、涡旋;而有些对流动的描述是基于基本变量得出的导出量,如等流函数线、等势线,或有些对流动的描述涉及的虽然是描述流动的直接变量,但不易直接观察,如压力波的传播,这些概念或现象较为抽象。对于描述流动较为抽象的概念若能用数学的方法加以量化,定量表示,则有助于加深对流体力学基本知识的理解、掌握和运用 [11] 。
3. 简单管路水击的数值解
3.1. 管路水击的数学描述
对于有压输水管道,当管道中的阀门突然关闭,或输水泵突然停止工作时会引起管道内压强和水的流速发生周期性的变化,造成管道振动并伴有噪声,危害管道安全或泵的正常运转。定水头输水管道可用图1表示。假设管内流动为一维流动,考虑管壁为弹性,流体有黏性时管内压力波从阀门到管道入口经历五次往返后,紧贴阀门处流体压强随时间的变化如图2所示。

Figure 1. A simple pipe with a constant hydrostatic head at inlet
图1. 入口静压水头为定值的简单管道

Figure 2. Graph of fluid pressure variation with time in front of pipeline valve
图2. 管道阀门前流体压强随时间变化示意图
在一维流动的假设下,若要定量分析管道某处压强、速度随时间的变化则需采用适当的数值方法。这里采用特征线法分析图1所示管道在阀门关闭时间为ΔT,黏性流体在管道内某处压强和速度随时间的变化规律。设管道直径为d,从管道入口到处管道长度为L从管道中距入口x处取一长为δx的微元段,左右截面速度、压强、静压水头如图3所示。以该微元管段为研究对象,应用牛顿第二定律和质量守恒原理可得微元管段内流体的动量方程和连续性方程。
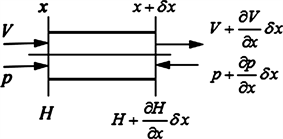
Figure 3. Microelement of the pipe
图3. 微元管段
动量方程和连续性方程分别见式(1)和式(2) [12] 。
(1)
(2)
以上两式中,g为重力加速度,a为压强波的传播速度, ,K为水的体积弹性模量,ρ为水的密度,E为管壁材料的弹性模量,s为管壁厚度。
式(1)和式(2)为一维、瞬态、非线性方程,定解条件包括热物性条件、初始条件和边界条件。这里假定水的体积弹性模量、密度、管壁材料的弹性模量为常数。
初始条件由式(3)表示:
(3)
边界条件由式(4)表示:
(4)
3.2. 特征线法及数值计算格式
特征线法是求解双曲型偏微分方程的一种近似计算方法,沿特征线方向可将偏微分方程转化为常微分方程,使原问题得到简化,也便于学生理解和掌握。由于对流项 相对于 和水头沿x的变化 相对于 均较小,从式(1)和式(2)中分别略去 和 ,可使方程得到进一步简化。简化后的方程表示为:
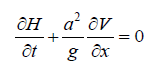 (5)
(5)
(6)
用常数因子 乘式(6),再与式(5)相加,得:
(7)
取 或 ,则式(7)可进一步表式为:
(8)
或:
(9)
(10)
对应两条特征线,即: 和 ,该两条特征线分别与式(9)和式(10)对应。在x-t平面上,同一时刻从两不同点M1和M2出发的两条特征线相较于P点,如图4所示。

Figure 4. A characteristic line from two points
图4. 从两点出发的特征线
在图4中,M1M = MM2 = Δx,MP = Δt。分别对式(9)和式(10)沿特征线积分,得:
(11)
(12)
令 , , ,由式(11)和式(12)可得:
(13)
(14)
对管道及求解时间进行划分,利用式(13)和式(14)便可计算出每一时层右行、左行特征线交点P处水的流速和水头。
3.3. 简单管路水击数值计算实例
取管道直径D = 250 mm,管道长度L = 500 m,水池静力水头H0 = 50 m,管内流体与壁面摩擦阻力系数f = 0.1,压强波传播速度a = 1000 m/s。将管道长度分割NX = 100份,Δx = 500/100 = 5 m,时间间隔Δt = Δx/a = 0.005 s,计算时间T = 30 s,关阀时间ΔT = 1.2 s。对于给定的管长和压强波传播速度,压强波从阀门前至管道入口传播一个管长经历的时间为0.5 s,由于ΔT > 2L/a = 1 s,故计算的工况属于间接水击。
应用MATLAB语言编程,对内部节点,式(13)、式(14)对应的程序语句为:
for I=2:NODES-1
A3=9.8/a;
A1=V(I-1)+A3*H(I-1)-1000*F*DELT/(2.0*D)*V(I-1)*abs(V(I-1));
A2=V(I+1)-A3*H(I+1)-1000*F*DELT/(2.0*D)*V(I+1)*abs(V(I+1));
VNEW(I)=(A1+A2)/2.0;
HNEW(I)=(A1-A2)/(2.0*A3);
end
管道入口边界条件对应的程序语句为:
HNEW(1)=H0;
VNEW(1)=V(2)+A3*(HNEW(1)-H(2))-1000*F*DELT/(2.0*D)*V(2)*abs(V(2));
阀门前边界条件对应的程序语句为:
if T>TCLOSE
VNEW(NODES)=0.0;
else
VNEW(NODES)=V0*(1.-T/TCLOSE);
end
HNEW(NODES)=H(NX)+(V(NX)-VNEW(NX)-1000*F*DELT/(2.0*D)*V(NX)*…
abs(V(NX))/A3;% NODES= NX+1
运行程序得管道x = L/2处水流速和阀门前压头随时间变化曲线如图5和图6所示。
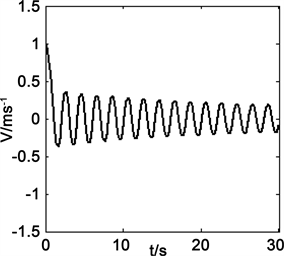
Figure 5. Variation of water velocity with time at x = L/2
图5. x = L/2处水流速随时间的变化
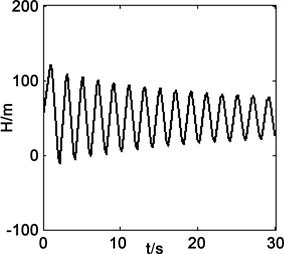
Figure 6. Variation of head with time in front of valve
图6. 阀门前水头随时间的变化
由于流体黏性的影响,水流速和压头随时间的增加而衰减,最大压头出现在第一个波峰处,Hmax = 121.56 m,对应的时间为t = 1.005 s。改变关阀时间,阻力系数等参数可获得其他工况下管内水流速、压力水头随时间的变化曲线,可加深对水击现象的认识和理解。
4. 结束语
根据我校《流体力学》课程教学大纲,水击现象的内容虽不属于课程的重点内容,但属于难点问题。所选用教材 [8] 对管道壁面材料为弹性,不考虑水的黏性,阀门突然关闭时的水击现象进行了定性介绍,导出了水压强增量、压强波传播速度的计算公式,定性介绍了直接水击和间接水击的概念。通过对水击现象的数值分析可定量分析不同工况下管道发生水击时水的流速和压强的变化,借助于数值计算结果能更生动、直观地了解水击过程。基于特征线法的简单管路水击分析计算程序短小,涉及的数学知识和编程方法学生能够理解和掌握。在工程基础类课程中不断引入数学、计算机编程等知识和方法不仅为理解和掌握后续《计算流体动力学》课程涉及的相关计算流体动力学软件的应用打下一定基础,也有助于循序渐进地培养和提高学生解决工程复杂问题的能力。
基金项目
感谢兰州交通大学“百名青年优秀人才培养计划”基金和甘肃省杰出青年基金(No. 1506RJDA061)的资助。
文章引用
林志敏,张永恒,王良璧. 运用数值计算方法和工具深化《流体力学》课程教学内容
Using Numerical Methods and Tools to Deepen the Teaching Content of “Fluid Mechanics” Course[J]. 教育进展, 2019, 09(03): 217-224. https://doi.org/10.12677/AE.2019.93037
参考文献
- 1. 人民网. 我国846个专业进入全球工程教育第一方阵[EB/OL]. http://gongyi.people.com.cn/n1/2018/0613/c151132-30054373.html, 2018-06-13.
- 2. 中国工程教育认证协会. 工程教育认证标准(机械类专业认证标准,2017年11月修订) [EB/OL]. http://meea.cmes.org/article?id=4, 2018-06-22.
- 3. 薛向东, 陈勇民, 童芸芸, 等. 基于专业认证的流体力学教学实践[J]. 浙江科技学院学报, 2018, 30(6): 517-522.
- 4. 林健. 如何理解和解决复杂工程问题——基于《华盛顿协议》的界定和要求[J]. 高等工程教育研究, 2016(5): 17-26+38.
- 5. 陶吉利, 李林功,蔡卫明, 等. 基于复杂工程问题能力培养的嵌入式课程群体系改革[J]. 安徽电子信息职业技术学院学报, 2018, 17(6): 1-4.
- 6. 杨扬, 张勤星, 王利霞, 等. 工科流体力学教学方法与改革[J]. 大学教育, 2015(6): 129-130.
- 7. 刘海涛, 卢毓俊, 李萍. 浅谈新工科背景下车辆工程专业流体力学课程教学改革实践[J]. 高校论坛, 2018(26): 6-8.
- 8. 孔珑. 工程流体力学[M]. 第四版. 北京: 中国电力出版社, 2017.
- 9. 景思睿. 流体力学[M]. 西安: 西安交通大学出版社, 2008.
- 10. 陈卓如, 王洪杰, 刘全忠, 等. 工程流体力学[M]. 北京: 高等教育出版社, 2013.
- 11. 陈国玉. 基于MATLAB在流体力学中的数值分析[J]. 哈尔滨师范大学自然科学学报, 2015, 31(6): 64-63+76.
- 12. Ghidaoui, M.S., Zhao, M., McInnis, D.A., et al. (2005) A Review of Water Hammer Theory and Practice. Applied Mechanics Reviews, 58, 50-76. https://doi.org/10.1115/1.1828050
NOTES
*通讯作者。