Pure Mathematics
Vol.4 No.05(2014), Article ID:14051,6 pages
DOI:10.12677/PM.2014.45026
An Elementary Proof for the Uniqueness (up to Isomorphism) of the Simple Groups of Order 360 and 504
1Department of Mathematics, Hubei University, Wuhan
2Department of Mathematics, Peking University, Beijing
Email: thoufeng@163.com, *ghliu@hubu.edu.cn
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Jul. 12th, 2014; revised: Aug. 10th, 2014; accepted: Aug. 19th, 2014
ABSTRACT
Only by using Sylow’s theorem, basic permutation computation and linear algebra theory, we prove that a simple group of order 360 is isomorphic to PSL (2,9) and a simple group of order 504 is isomorphic to PSL (2,8).
Keywords:Sylow’s Theorem, Simple Group, PSL (2,9), PSL (2,8)

360阶和504阶单群的唯一性的初等群论证明
周 峰1,于浩然2,王 杰2,刘合国1*
1湖北大学数学系,武汉
2北京大学数学系,北京
Email: thoufeng@163.com, *ghliu@hubu.edu.cn
收稿日期:2014年7月12日;修回日期:2014年8月10日;录用日期:2014年8月19日

摘 要
仅用Sylow定理、最基本的置换计算和线性代数重新证明了360阶单群同构于PSL (2,9)及504阶单群同构于PSL (2,8)。
关键词
Sylow定理;单群;PSL (2,9),PSL (2,8)

1. 引言
本文采用的符号和术语都是标准的,见文献[1] 。
我们知道,对![]() 阶的非交换单群,当
阶的非交换单群,当 时,
时,![]() 只能是60、168、360、504、660,并且阶不超过1000的非交换单群只有5个:60阶单群
只能是60、168、360、504、660,并且阶不超过1000的非交换单群只有5个:60阶单群 、168阶单群
、168阶单群 、360阶单群
、360阶单群 、504阶单群
、504阶单群 和660阶单群
和660阶单群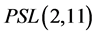 。运用Sylow定理不难证明60阶单群同构于
。运用Sylow定理不难证明60阶单群同构于 ,见文献[2] 和[3]
。在文献[2] 和[3] 中,Huppert和Smith分别用不同的初等群论方法证明了168阶单群同构于
,见文献[2] 和[3]
。在文献[2] 和[3] 中,Huppert和Smith分别用不同的初等群论方法证明了168阶单群同构于 ,而360阶单群同构于的
,而360阶单群同构于的 初等群论证明见[4] [5] ,[6] 利用文献[2]
的方法证明了660阶单群同构于
初等群论证明见[4] [5] ,[6] 利用文献[2]
的方法证明了660阶单群同构于 。对于504阶单群同构于
。对于504阶单群同构于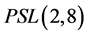 ,在[5] 中,Cole利用置换群的技巧给出了证明。这样,阶不超过1000的非交换单群同构唯一性都有了初等的群论证明。而本文将利用[2]
和[6] 里的方法,从射影线性群的角度出发,将360阶单群及504阶单群里的某些元素与射影线性群里的元素对应起来,从而将给定阶的单群嵌入射影线性群里,再通过比较群的阶,重新证明360阶单群同构于
,在[5] 中,Cole利用置换群的技巧给出了证明。这样,阶不超过1000的非交换单群同构唯一性都有了初等的群论证明。而本文将利用[2]
和[6] 里的方法,从射影线性群的角度出发,将360阶单群及504阶单群里的某些元素与射影线性群里的元素对应起来,从而将给定阶的单群嵌入射影线性群里,再通过比较群的阶,重新证明360阶单群同构于 及504阶单群同构于
及504阶单群同构于 。除了Sylow定理和最基本的群论知识外,本文是完全自包含的,这个证明对初学者来说是容易理解的,作者希望它对群论教学具有借鉴和启发作用。
。除了Sylow定理和最基本的群论知识外,本文是完全自包含的,这个证明对初学者来说是容易理解的,作者希望它对群论教学具有借鉴和启发作用。
2. 360阶单群同构于 的初等群论证明
的初等群论证明
证明:设G是360阶单群。
(1) 。由Sylow第三定理知
。由Sylow第三定理知 1,6或36。由G是单群,
1,6或36。由G是单群, 不可能为1。谬设
不可能为1。谬设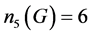 ,由G是360阶单群,
,由G是360阶单群, ,而
,而 ,矛盾!
,矛盾!
(2) 若 且
且 ,则
,则 。谬设
。谬设 ,则
,则 。从而
。从而 。从而
。从而 。由于G是360阶单群,
。由于G是360阶单群, 。不难看出
。不难看出 中之4阶子群正规,设
中之4阶子群正规,设 ,则
,则 。不难看出
。不难看出 或4,且
或4,且

 ,从而
,从而 。若
。若 ,则
,则 中有9阶子群正规,进而知
中有9阶子群正规,进而知 中9阶子群正规,矛盾!若
中9阶子群正规,矛盾!若 ,则
,则 ,矛盾于G是360阶单群!
,矛盾于G是360阶单群!
(3) 。由Sylow第三定理知
。由Sylow第三定理知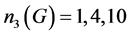 或40。由G是360阶单群,
或40。由G是360阶单群,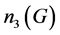 不可能为1或4。若
不可能为1或4。若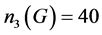 ,则由1、2知G中至少有
,则由1、2知G中至少有 个元素,矛盾!故
个元素,矛盾!故 。取定
。取定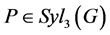 ,则
,则 。
。
(4) G中无6阶元及10阶元。谬设G中有6阶元x。注意到G依共轭作用在 上诱导G到
上诱导G到 的群嵌入。承2知
的群嵌入。承2知 引起的置换同形于
引起的置换同形于 。从而x引起的置换同形于
。从而x引起的置换同形于 ,是奇置换,矛盾!谬设G中有10阶元y,同样注意到G依共轭作用在
,是奇置换,矛盾!谬设G中有10阶元y,同样注意到G依共轭作用在 上诱导G到
上诱导G到 的群嵌入,且由3知y引起的置换无不动点。从而y引起的置换同形于
的群嵌入,且由3知y引起的置换无不动点。从而y引起的置换同形于 ,是奇置换,矛盾!
,是奇置换,矛盾!
(5) 且
且 是Frobenius群,
是Frobenius群, 在
在 中的补群是4阶循环群。谬设
中的补群是4阶循环群。谬设 。由于
。由于 ,故
,故 中有6阶元,矛盾于(4)。亦承(4)知
中有6阶元,矛盾于(4)。亦承(4)知 是36阶Frobenius群,进一步地,
是36阶Frobenius群,进一步地, 在
在 中的补群是4阶循环群。
中的补群是4阶循环群。
(6) 依共轭正则地作用在
依共轭正则地作用在 上。从而
上。从而 在
在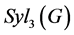 上的传递的共轭作用置换同构于9元域
上的传递的共轭作用置换同构于9元域 上的射影空间上的置换群
上的射影空间上的置换群
 。
。
 的行列式都是
的行列式都是 中的平方元,故
中的平方元,故 嵌入
嵌入 。
。
(7) 首先证明G之Sylow 2-子群同构于 。取定
。取定 ,谬设
,谬设 交换,由于G中有4阶循环子群,故
交换,由于G中有4阶循环子群,故 或
或 。由4知
。由4知 ,且
,且 之任一非单位元
之任一非单位元 都满足
都满足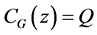 ,进而
,进而 在G中的共轭类长
在G中的共轭类长 。如果
。如果 使得
使得 。则
。则 ,从而
,从而 。从而G共有
。从而G共有 个2-元素。G中至少有
个2-元素。G中至少有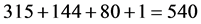 个元素,矛盾!谬设
个元素,矛盾!谬设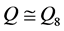 ,设
,设
![]() 诱导的置换是
诱导的置换是 。
。 使得
使得 。则
。则 引起的置换的不动点只有
引起的置换的不动点只有 ,
,![]() 引起的置换对换
引起的置换对换 。从而
。从而![]() 诱导的置换同形于
诱导的置换同形于 ,是奇置换,矛盾!故
,是奇置换,矛盾!故 。
。
(8) 由于 ,故
,故 使得
使得 ,则
,则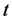 对换
对换 。以下简记
。以下简记![]() 为
为![]() 。则
。则 诱导的置换:
诱导的置换:

由于 诱导的是偶置换,故
诱导的是偶置换,故 或
或![]() 。
。
若 ,则
,则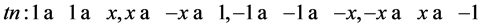 ,
, 且
且 ,故可以用
,故可以用 替代
替代 。
。
若 ,则
,则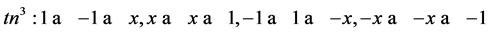 ,同理以用
,同理以用 替代
替代 。
。
若 ,则
,则 ,同理以用
,同理以用 替代
替代 。
。
故无妨设 ,
, 。
。
同理 或
或 。
。
若 ,则
,则

考虑平移( 中某3阶元诱导)
中某3阶元诱导) :
:
则 (先作用
(先作用 ,后作用
,后作用 ):
):
即 ,是21阶元,但21不整除360,矛盾!
,是21阶元,但21不整除360,矛盾!
若 ,则
,则
即 ,是奇置换,矛盾!
,是奇置换,矛盾!
若 ,则
,则
即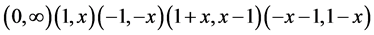 ,亦是奇置换,矛盾!
,亦是奇置换,矛盾!
从而 ,
,
亦即 。可由
。可由 诱导。由于
诱导。由于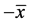 是
是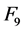 中之平方元,故
中之平方元,故 嵌入
嵌入 。由于
。由于 ,从而
,从而 ,
, 可嵌入
可嵌入 中,再比较群的阶,得
中,再比较群的阶,得 。
。
3. 关于
为了讨论504阶单群的唯一性,我们从 的元素和Sylow子群入手。
的元素和Sylow子群入手。
首先注意到 ,我们通过弄清
,我们通过弄清 的结构来得到
的结构来得到 的相关信息。
的相关信息。
(1)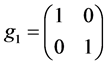 是
是 的单位元。
的单位元。
(2)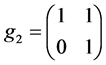 为
为 的一个2阶元,若有
的一个2阶元,若有 使
使 ,则
,则 ,因此
,因此 ,
, ,
, 。考虑到
。考虑到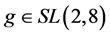 ,
, ,此时
,此时 ,
, ,
, ,
, ,
, 所在的共轭类长为63。
所在的共轭类长为63。
(3) 为
为 上不可约多项式,不妨设
上不可约多项式,不妨设 ,令
,令 ,则
,则![]() 为7阶元。当
为7阶元。当 时,
时, ;当
;当 时,
时, ;当
;当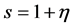 时,
时, 。令
。令 ,
, ,
, ,易知
,易知 ,
, ,
, 均为7阶元,若有
均为7阶元,若有 使
使 ,则
,则 ,此时
,此时 ,因此
,因此 ,其中
,其中 。容易得到
。容易得到 ,
, 所在的共轭类长72,同样的计算可得
所在的共轭类长72,同样的计算可得 ,
, 所在的共轭类长分别为72。
所在的共轭类长分别为72。
(4) 上首一2次的常数项为1的不可约多项式有
上首一2次的常数项为1的不可约多项式有
 ,
, ,
, ,
,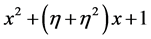
四个多项式对应的相伴矩阵分别为
 ,
, ,
, ,
,
可选取 的一个生成元
的一个生成元![]() 使
使 ,此时
,此时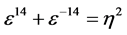 ,
, 且
且 ,因此
,因此 ,
, ,
,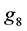 ,
, 均可表成形如
均可表成形如 的矩阵。
的矩阵。
若有 使
使 则
则 ,
, ,另外,
,另外, 。令
。令 ,由于
,由于 当且仅当
当且仅当 ,因此
,因此 。令
。令 ,若
,若 (其中
(其中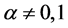 ),
), 里的每个元都是平方元,故存在
里的每个元都是平方元,故存在 使
使 ,此时
,此时 ,
, ,此时
,此时 的取法种数为
的取法种数为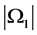 。因此
。因此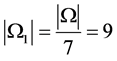 ,即
,即 ,
, ,
,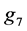 ,
, ,
, 所在的共轭类长都是56。
所在的共轭类长都是56。
综上所述,考虑到 、
、 、
、 、
、 、
、 、
、 、
、 和
和 具有不同的迹,它们彼此不相似,而
具有不同的迹,它们彼此不相似,而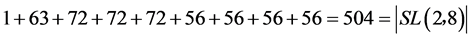 ,这说明我们已经找出了
,这说明我们已经找出了 的所有共轭类,综合(1)、(2)、(3)、(4),我们得到
的所有共轭类,综合(1)、(2)、(3)、(4),我们得到 的元素的信息(如表1)。
的元素的信息(如表1)。
由于 ,所以
,所以 也具有同样的共轭类。
也具有同样的共轭类。
现在,我们能够很快证明 是一个单群。事实上,任取
是一个单群。事实上,任取 的正规子群
的正规子群 ,
, 的阶整除504,且
的阶整除504,且 ,其中
,其中 或1,
或1,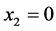 、1、2或3,
、1、2或3, 、1、2、3或4。不难验证
、1、2、3或4。不难验证 或504,即
或504,即 或
或 ,
,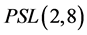 是单群。
是单群。
(5) 令 ,此时
,此时 为初等Abel群且
为初等Abel群且 ,由于
,由于 为
为 的7阶元且
的7阶元且 ,故7整除
,故7整除 ,再考虑到8整除
,再考虑到8整除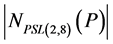 及
及 是单群,所以
是单群,所以 ,
, 的Sylow
2-子群的个数
的Sylow
2-子群的个数 。
。
(6) 由于 有9阶元,故
有9阶元,故 的Sylow 3-子群
的Sylow 3-子群 为循环群,
为循环群, 包含6个9阶元,而
包含6个9阶元,而 含有
含有 个9阶元,我们得到
个9阶元,我们得到 的Sylow
3-子群的个数
的Sylow
3-子群的个数 ,
, 。
。
(7)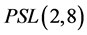 的Sylow 7-子群
的Sylow 7-子群 为循环群,
为循环群, 包含6个7阶元,而
包含6个7阶元,而 含有
含有 个7阶元,我们得到
个7阶元,我们得到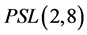 的Sylow
7-子群的个数
的Sylow
7-子群的个数 ,
, 。
。
综上所述,我们得到 的Sylow子群
的Sylow子群 的如下信息:
的如下信息:
这些信息有助于我们弄清504阶单群的Sylow子群及其正规化子的结构。
表1. SL(2,8)的共轭类
4. 504阶单群同构于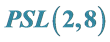 的初等群论证明
的初等群论证明
证明:设 是504阶单群,此时
是504阶单群,此时 。
。
(1) 。令
。令 ,由Sylow定理知
,由Sylow定理知 和
和 ,因此
,因此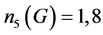 或36。注意到
或36。注意到 为单群,
为单群, 或36。谬设
或36。谬设 ,则
,则 ,
, 为
为 的指数为8的子群,这时容易验证
的指数为8的子群,这时容易验证 嵌入
嵌入 。容易知道
。容易知道 的7阶元有
的7阶元有 个,
个, 的Sylow
7-子群有
的Sylow
7-子群有
 个,进一步地,
个,进一步地, ,而
,而 ,这是不可能的!所以只能有
,这是不可能的!所以只能有 ,
, ,这时,
,这时,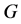 有
有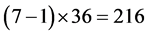 个7阶元。
个7阶元。
(2) 。取
。取 ,由Sylow定理
,由Sylow定理 或28。注意到
或28。注意到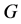 是单群,所以
是单群,所以 或28。谬设
或28。谬设 ,则
,则 同构于
同构于 的一个子群,而
的一个子群,而 ,故
,故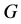 是
是 的指数为5的子群,此时
的指数为5的子群,此时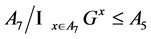 ,
, 是单群,只能有
是单群,只能有 ,即
,即 ,此时
,此时 的7阶元全部在
的7阶元全部在 里,而
里,而 含有
含有 个7阶元,
个7阶元, 含有216个7阶元,矛盾!于是只能有
含有216个7阶元,矛盾!于是只能有 ,
,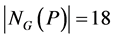 。
。
(3) 的任意两个不同的Sylow 3-子群有平凡的交。选取不同的
的任意两个不同的Sylow 3-子群有平凡的交。选取不同的 。谬设
。谬设 ,则
,则 且
且 ,显然
,显然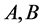 都是
都是 的Sylow
3-子群,
的Sylow
3-子群, 的Sylow 3-子群个数
的Sylow 3-子群个数
 且9整除
且9整除 。又
。又 ,
, 。考虑到
。考虑到 的真子群指数
的真子群指数
大于7,不难验证 或63。如
或63。如 ,
, 的Sylow 7-子群正规,而
的Sylow 7-子群正规,而 的Sylow 7-子群的正规化子为14阶,这是不可能的!如
的Sylow 7-子群的正规化子为14阶,这是不可能的!如 ,
, 是12阶群,
是12阶群, 的Sylow
3-子群肯定不是正规的,由Sylow定理知,
的Sylow
3-子群肯定不是正规的,由Sylow定理知, 包含4个Sylow 3-子群,它包含8个3阶元,故
包含4个Sylow 3-子群,它包含8个3阶元,故 的Sylow 2-子群是正规的。设
的Sylow 2-子群是正规的。设 是
是 的Sylow
2-子群,
的Sylow
2-子群, ,取
,取![]() 的Sylow 2-子群
的Sylow 2-子群 ,
, 是4阶群,
是4阶群, 。从
。从 知,
知, ,
, 是
是![]() 的中心。当
的中心。当 时,
时, 是
是 的Sylow
2-子群,故
的Sylow
2-子群,故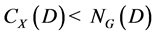 ,
, 是18阶群,它有正规的Sylow
3-子群,这将导致
是18阶群,它有正规的Sylow
3-子群,这将导致 含有正规的Sylow 3-子群,矛盾,因此只能有
含有正规的Sylow 3-子群,矛盾,因此只能有 。当
。当 时,
时,![]() 是12阶Abel群,
是12阶Abel群, 是
是![]() 的特征子群,
的特征子群, 。又取
。又取 的包含
的包含 的Sylow
2-子群
的Sylow
2-子群 ,当然
,当然 ,从而
,从而 ,
, 能被
能被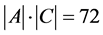 整除,
整除, 或7,这是不可能的!因此
或7,这是不可能的!因此 ,这表明
,这表明 的任意两个不同的Sylow
3-子群有平凡的交,
的任意两个不同的Sylow
3-子群有平凡的交,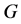 含有
含有 个3-元。
个3-元。
(4) 。取
。取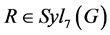 ,
, ,谬设
,谬设 的Sylow
2-子群正规,则
的Sylow
2-子群正规,则 为14阶循环群,含
为14阶循环群,含 的14阶元,故
的14阶元,故 一共包含
一共包含 个14阶元,而
个14阶元,而 含有216个7阶元,224个3-元,
含有216个7阶元,224个3-元, ,矛盾!因此
,矛盾!因此 的Sylow
2-子群的个数
的Sylow
2-子群的个数 。
。
(5) 所含的2-元均为2阶元。考虑
所含的2-元均为2阶元。考虑 作用在
作用在 ,
, 含有一个7阶子群并含有7个2阶子群,其中任意2阶元将7阶元映到它的逆,任意7阶元在
含有一个7阶子群并含有7个2阶子群,其中任意2阶元将7阶元映到它的逆,任意7阶元在 上引起的置换为5个不相交轮换的乘积,我们可以得到这个2阶元刚好在其中3个轮换中各有一个不动点,这样,这个2阶元刚好有4
上引起的置换为5个不相交轮换的乘积,我们可以得到这个2阶元刚好在其中3个轮换中各有一个不动点,这样,这个2阶元刚好有4
个不动点。此时,这个2阶元所在的共轭类长为 ,我们得到63个共轭的2阶元。由于
,我们得到63个共轭的2阶元。由于 含有
含有
216个7阶元,224个3-元,剩下 个非单位元,所以这63个非单位元全为2阶元,并且它们彼此共轭。
个非单位元,所以这63个非单位元全为2阶元,并且它们彼此共轭。
(6) 。令
。令 ,由于
,由于 所含的2-元均为2阶元,因此
所含的2-元均为2阶元,因此 为初等Abel群。由Sylow定理知
为初等Abel群。由Sylow定理知 和
和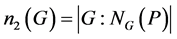 ,因此
,因此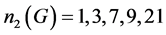 或63。注意到
或63。注意到 为单群,
为单群, 或63。谬设
或63。谬设 ,则
,则 。由Sylow定理得
。由Sylow定理得 或4,
或4, 最多含有
最多含有 个3阶元,但
个3阶元,但 ,
, 含有7个2-元,
含有7个2-元, ,这表明
,这表明 一定包含6阶元,由前面的讨论知这是不可能的!谬设
一定包含6阶元,由前面的讨论知这是不可能的!谬设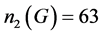 ,则
,则 。取不同的2阶元
。取不同的2阶元 ,由前面的讨论,有
,由前面的讨论,有 使
使 ,考虑到
,考虑到 为初等Abel群,
为初等Abel群, ,而
,而 ,故
,故 ,即
,即 ,而
,而 ,因此
,因此 ,
,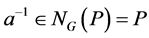 ,这就得到了
,这就得到了 ,矛盾!这时只能有
,矛盾!这时只能有 ,
, 。
。
(7) 首先证明 。由于
。由于 含有63个2阶元,9个Sylow 2-子群,因而
含有63个2阶元,9个Sylow 2-子群,因而 的不同的Sylow 2-子群交平凡,由于
的不同的Sylow 2-子群交平凡,由于 ,谬设
,谬设 ,则
,则 有
有 个56阶元,故
个56阶元,故 一共包含
一共包含 个56阶元,而
个56阶元,而 含有216个7阶元,224个3-元,
含有216个7阶元,224个3-元, ,矛盾!因此
,矛盾!因此 的Sylow
7-子群的个数
的Sylow
7-子群的个数 。
。
从而 在
在 上的传递的共轭作用置换同构于8元域
上的传递的共轭作用置换同构于8元域 上的射影空间上的置换群
上的射影空间上的置换群

设 是
是 的7阶子群,则
的7阶子群,则 ,取2阶元
,取2阶元 ,由于
,由于 与
与![]() 不交换,故
不交换,故 ,按照[6]
同样的方法,可得
,按照[6]
同样的方法,可得 作用在
作用在 上的置换为
上的置换为 ,由
,由 里的所有元都是平方元及
里的所有元都是平方元及

所以![]() 、
、![]() 、
、 对应的线性分式映射属于
对应的线性分式映射属于 。
。
令 ,
, 作为
作为 的子群可嵌入
的子群可嵌入 ,其中
,其中 为56阶群且
为56阶群且 为不属于
为不属于 的2阶元,故
的2阶元,故 ,即
,即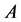 是
是 的指数小于9的子群,再注意到
的指数小于9的子群,再注意到 为单群,于是
为单群,于是 ,故
,故 可嵌入
可嵌入 ,而
,而 ,因此
,因此 。
。
基金项目
国家自然科学基金(11371124)、湖北省高层次人才工程基金(070-016533)。
参考文献 (References)
- [1] Isaacs, I.M. (2008) Finite group theory. American Mathematical Society, Providence.
- [2] Huppert, B. (1967) Endliche gruppen. Springer-Verlag, Berlin, Heidelberg, New York.
- [3] Smith, G. and Tabachnikova, O. (2000) Topics in group theory. Springer-Verlag, Berlin, Heidelberg, New York.
- [4] 周峰, 徐行忠, 廖军, 刘合国 (2014) 360阶单群同构于A6的初等群论证明. 理论数学, 1, 31-37.
- [5] Cole, F.N. (1893) Simple groups as far as order 660. American Journal of Mathematics, 15, 303-315.

NOTES
*通讯作者。
