Pure Mathematics
Vol.05 No.02(2015), Article ID:14904,7
pages
10.12677/PM.2015.52007
Weighted Lp Estimates for the Bi-Harmonic Parabolic Equation
Huacui Yu
College of Sciencers, Shanghai University, Shanghai
Email: 15202161183@163.com
Received: Feb. 18th, 2015; accepted: Feb. 27th, 2015; published: Mar. 3rd, 2015
Copyright © 2015 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Schauder estimates and  estimates are the basic regularity estimates in the partial differential equations. In this paper we mainly study a new class of regularity estimates, weighted
estimates are the basic regularity estimates in the partial differential equations. In this paper we mainly study a new class of regularity estimates, weighted  estimates for the bi-harmonic parabolic equation.
estimates for the bi-harmonic parabolic equation.
Keywords:Bi-Harmonic Parabolic Equation, Weighted,  Estimates, Regularity Estimates
Estimates, Regularity Estimates

双调和抛物方程的加权Lp估计
于华翠
上海大学理学院,上海
Email: 15202161183@163.com
收稿日期:2015年2月18日;录用日期:2015年2月27日;发布日期:2015年3月3日

摘 要
Schauder估计和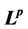 估计是偏微分方程基本的正则性估计。本文我们主要研究双调和抛物方程的一类新的正则性估计——加权
估计是偏微分方程基本的正则性估计。本文我们主要研究双调和抛物方程的一类新的正则性估计——加权 估计。
估计。
关键词 :双调和抛物方程,加权, 估计,正则性估计
估计,正则性估计

1. 引言
微分方程解的存在唯一性及其正则性是偏微分方程中的经典问题,其中Schauder估计和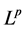 估计在正则性理论的研究中具有非常重要的作用。2003年,Wang [1] 在Caffarelli和Peral [2] 基础上利用紧方法、Vitali覆盖引理、极大函数等技巧给出了Poisson方程和热传导方程的
估计在正则性理论的研究中具有非常重要的作用。2003年,Wang [1] 在Caffarelli和Peral [2] 基础上利用紧方法、Vitali覆盖引理、极大函数等技巧给出了Poisson方程和热传导方程的 内估计的几何化方法证明。之后,Byun和Wang利用类似的技巧在[3] -[7] 中得到了各类二阶散度型椭圆方程与抛物型方程在不同的区域(Reifenberg, Lipschitz)区域等中的全局
内估计的几何化方法证明。之后,Byun和Wang利用类似的技巧在[3] -[7] 中得到了各类二阶散度型椭圆方程与抛物型方程在不同的区域(Reifenberg, Lipschitz)区域等中的全局 估计。近几年,Mengesha和Phuc在[8] [9] 中应用类似的技术方法研究了散度型椭圆问题的全局加权
估计。近几年,Mengesha和Phuc在[8] [9] 中应用类似的技术方法研究了散度型椭圆问题的全局加权 估计。Byun,Palagachev和Ryu在文章[10] 中也讨论了散度型抛物方程在不光滑区域上的加权
估计。Byun,Palagachev和Ryu在文章[10] 中也讨论了散度型抛物方程在不光滑区域上的加权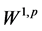 估计,另外,Yao在[11] 中讨论了
估计,另外,Yao在[11] 中讨论了 调和椭圆方程的梯度加权
调和椭圆方程的梯度加权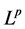 估计。我们的工作主要是把相应的结论推广到双调和抛物型方程以及更高阶的多调和抛物型方程。
估计。我们的工作主要是把相应的结论推广到双调和抛物型方程以及更高阶的多调和抛物型方程。
考虑下述四阶的双调和抛物方程S
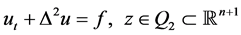 (1.1)
(1.1)
这里 ,而
,而 ,其中
,其中 。另外,我们记
。另外,我们记

这里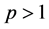 且
且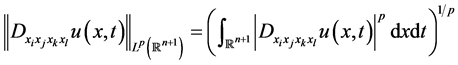 。
。
本文主要目的是得到问题(1.1)解 的如下估计
的如下估计
 (1.2)
(1.2)
这里 是不依赖于u和f的常数。事实上,如果
是不依赖于u和f的常数。事实上,如果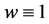 ,那么上述估计即为经典的
,那么上述估计即为经典的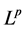 内估计。现在我们首先介绍一下加权空间的一些概念与性质(见[8] -[13] )。
内估计。现在我们首先介绍一下加权空间的一些概念与性质(见[8] -[13] )。
定义1.1. 假设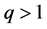 ,我们称权函数
,我们称权函数 ,如果
,如果 ,几乎处处
,几乎处处 ,且存在常数
,且存在常数 使得满足下述不等式
使得满足下述不等式

对任意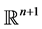 中的
中的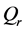 上成立。我们记
上成立。我们记

另外,相应的加权空间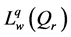 是由满足
是由满足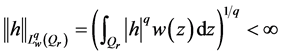 条件的全体函数h组成。
条件的全体函数h组成。
注1.2. 1) 事实上,我们可得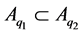 ,这里
,这里 。
。
2) 如果 ,那么,
,那么,
 任意
任意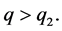
3) 如果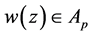 ,那么,
,那么, 。
。
4) 如果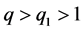 ,那么
,那么 。
。
我们进一步给出重要的反Hölder不等式和 权的一些其它性质。
权的一些其它性质。
引理1.3. 如果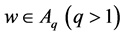 ,那么存在常数
,那么存在常数 ,使得对任意
,使得对任意 有
有

引理1.4. 如果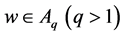 且
且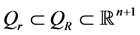 ,那么存在常数
,那么存在常数 有
有

引理1.5. 如果 且
且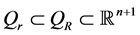 ,那么存在常数
,那么存在常数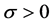 及
及 使得
使得

现在我们给出本文的主要结论。
定理1.6. 假设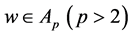 且
且 。如果
。如果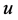 满足双调和抛物方程且
满足双调和抛物方程且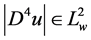 ,那么我们可得加权
,那么我们可得加权 估计(1.2)式。
估计(1.2)式。
注1.7. 上述定理的结论可以推广到更高阶的多调和抛物型方程,即方程
 (1.3)
(1.3)
有类似于定理1.6的加权 估计
估计
 (1.4)
(1.4)
2. 主要结论的证明
本节我们将完成主要结论定理1.6的证明。现在我们记
 (2.1)
(2.1)
这里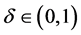 是一个充分小的待定正常数。令
是一个充分小的待定正常数。令
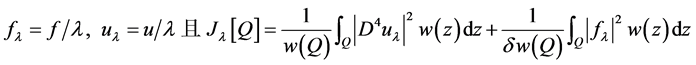 (2.2)
(2.2)
对任意的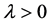 和
和 。另外,我们把水平集
。另外,我们把水平集 定义为
定义为
下面,我们将分解水平集 并给出相应的性质。
并给出相应的性质。
引理2.1. 任意给定 。如果
。如果 ,那么存在一族互不相交的
,那么存在一族互不相交的 ,使得
,使得
 (2.3)
(2.3)
且
 (2.4)
(2.4)
这里 且
且 。进一步,我们可得
。进一步,我们可得
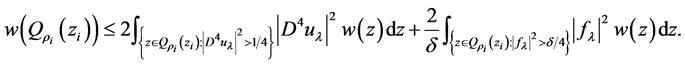 (2.5)
(2.5)
证明:1) 首先,对几乎处处的 ,由基本的测度理论我们可得
,由基本的测度理论我们可得
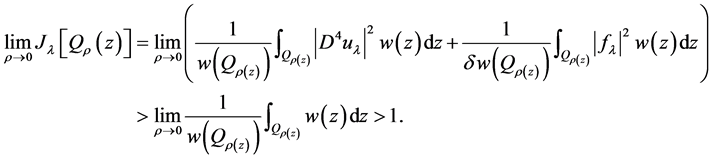
故存在某个 满足:
满足:
 (2.6)
(2.6)
另外,对某一固定的 ,且任意的
,且任意的 由(2.1)、(2.2)和引理1.4,可得
由(2.1)、(2.2)和引理1.4,可得
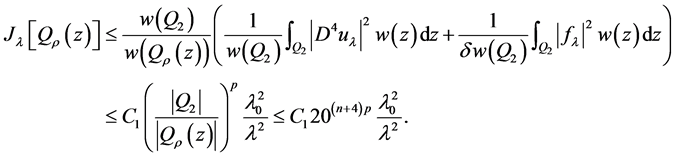
当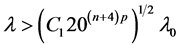 时,进一步可得:
时,进一步可得: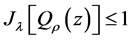 。
。
所以,我们有
 。
。
因此,由上式和(2.6)式可知,存在 使得:
使得:
 ,
, 任意的
任意的 。
。
综上所述,可得对几乎处处的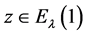 都存在满足如上条件的区域
都存在满足如上条件的区域 。然后,利用Vitali覆盖引理,我们找到一族互不相交的
。然后,利用Vitali覆盖引理,我们找到一族互不相交的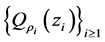 并且满足(2.3)和(2.4)。从而第一部分结论得证!
并且满足(2.3)和(2.4)。从而第一部分结论得证!
2) 由(2.2)和(2.3),可得:
 。
。
再将上式中右边的二个积分都拆为两项,可得

整理后即可得第二部分的结论!
事实上,由上面的引理可以得到如下两个不等式:
 (2.7)
(2.7)
 (2.8)
(2.8)
进一步,由上面的不等式我们还可以得如下引理。
引理2.2. 假设 且
且 。那么存在常数
。那么存在常数 使得
使得

证明:这里我们只证明第一式,第二式同理可证。对任意的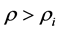 ,由Hölder不等式可得
,由Hölder不等式可得
 .
.
由定义1.1和(2.7)式,并且 ,可得
,可得
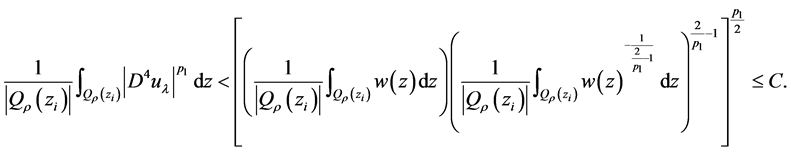
最后,我们将完成主要结论:定理1.6的证明。通过基本的逼近理论(见[14] -[17] ),我们不妨假设 。
。
证明:对于固定的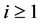 ,我们首先对
,我们首先对 作从
作从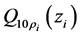 到
到 上的零延拓,并记为
上的零延拓,并记为 。则
。则 ,现在我们引入下述参照方程
,现在我们引入下述参照方程
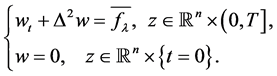
由 估计(见[18] ),我们可得:
估计(见[18] ),我们可得:
从而可得

由上式及引理2.2得
 (2.9)
(2.9)
令 ,可知
,可知 。
。
由引理2.2和(2.9)可得

故由基本的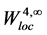 内部正则性理论(见[19] ),可得:
内部正则性理论(见[19] ),可得: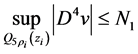 ,这里取
,这里取 。利用(2.9)和上式
。利用(2.9)和上式
我们可得
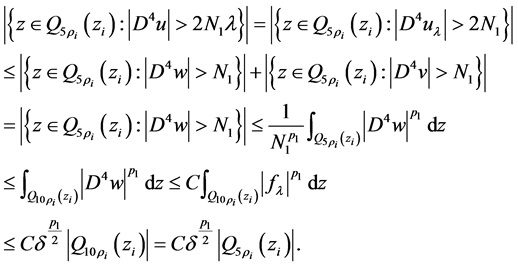
那么由引理1.4和引理1.5及上式,可得
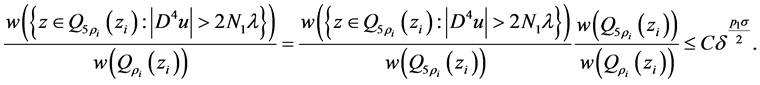
即:
 。
。
现在记 ,则对任意的
,则对任意的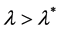 ,利用引理2.1中的(2.5)并将(2.2)式代入上式,可得
,利用引理2.1中的(2.5)并将(2.2)式代入上式,可得

又因为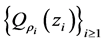 的互不相交性和
的互不相交性和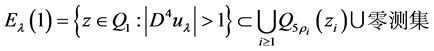 ,
,
我们可得:
 (2.10)
(2.10)
利用注1.2计算可得

 的估计。事实上,首先可得下面不等式
的估计。事实上,首先可得下面不等式

再结合 的定义,可得
的定义,可得
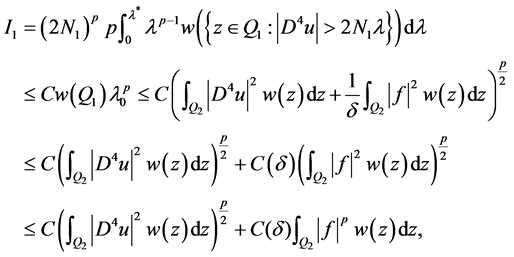
这里 是指仅依赖于
是指仅依赖于 的常数。
的常数。
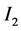 的估计,由于
的估计,由于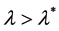 ,利用(2.10)及注1.2中的(2),可得
,利用(2.10)及注1.2中的(2),可得

结合 与
与 的估计,我们可得
的估计,我们可得

选取合适的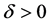 满足
满足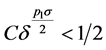 ,利用基本的迭代引理(见[19] [20] )吸收掉上式右端的第一个积分,从而可得
,利用基本的迭代引理(见[19] [20] )吸收掉上式右端的第一个积分,从而可得

再由方程(1.1)即可得定理1.6的结论。
基金项目
国家自然科学基金(11471207)。
文章引用
于华翠, (2015) 双调和抛物方程的加权Lp估计
Weighted Lp Estimates for the Bi-Harmonic Parabolic Equation. 理论数学,02,46-53. doi: 10.12677/PM.2015.52007
参考文献 (References)
- 1. Wang, L. (2003) A geometric approach to the Calderón-Zygmund estimates. Acta Mathematica Sinica (Engl. Ser.), 19, 381-396.
- 2. Caffarelli, L. and Peral, I. (1998) On W1,p estimates for elliptic equations in divergence form. Commu-nications on Pure and Applied Mathematics, 51, 1-21.
- 3. Byun, S. and Wang, L. (2004) Elliptic equations with BMO coefficients in Reifenberg domains. Communications on Pure and Applied Mathematics, 57, 1283-1310.
- 4. Byun, S. and Wang, L. (2005) Lp estimates for parabolic equations in Reifenberg domains. Journal of Functional Analysis, 223, 44-85.
- 5. Byun, S. and Wang, L. (2005) Parabolic equations in Reifenberg domains. Archive for Rational Mechanics and Analysis, 176, 271-301.
- 6. Byun, S. andWang, L. (2007) Parabolic equations in Time Dependent Reifenberg domains. Advances in Mathematics, 212, 797-818.
- 7. Byun, S. andWang, L. (2007) Quasilinear elliptic equations with BMO coefficients in Lipschitz domains. Transactions of the American Mathematical Society, 359, 5899-5913.
- 8. Mengesha, T. and Phuc, N. (2011) Weighted and regularity estimates for nonlinear equations on Reifenberg flat domains. Journal of Differential Equations, 250, 2485-2507.
- 9. Mengesha, T. and Phuc, N. (2012) Global estimates for quasilinear elliptic equations on Reifenberg flat domains. Archive for Rational Mechanics and Analysis, 203, 189-216.
- 10. Byun, S., Palagachev, D. and Ryu, S. (2013) weighted W1,p estimates for solutions of non-linear parabolic equations over non-smooth domains. Bulletin of the London Mathematical Society, 45, 765-778.
- 11. Yao, F.P. (2014) Weighted gradient estimates for the general elliptic p(x)-Laplacian equations. Journal of Mathematical Analysis and Applications, 415, 644-660.
- 12. Yao, F.P. (2014) Weighted Lp estimates for the elliptic Schrödinger operator. Journal of Mathematical Analysis and Applications, 33, 1-13.
- 13. 周民强 (2003) 调和分析讲义(实变方法). 北京大学出版社, 北京.
- 14. Acerbi, E. and Mingione, G. (2007) Gradient estimates for a class of parabolic systems. Duke Mathematical Journal, 136, 285-320.
- 15. Byun, S., Yao, F.P. and Zhou, S.L. (2008) Gradient estimates in Orlicz space for nonlinear elliptic equations. Journal of Functional Analysis, 255, 1851-1873.
- 16. Byun, S. and Ryu, S. (2013) Global weighted estimates for the gradient of solutions to nonlinear el-liptic equations. Annales de l’Institut Henri Poincare (C) Non Linear Analysis, 30, 291-313.
- 17. Wang, L.H., Yao, F.P., Zhou, S.L. and Jia, H.L. (2009) Optimal regularity for the poisson equation. Proceedings of the American Ma-thematical Society, 137, 2037-2047.
- 18. Yao, F.P. and Zhou, S.L. (2008) Global Lp estimates for the parabolic equa-tion of the Bi-harmonic type. Journal of Partial Differential Equations, 21, 315-334.
- 19. Evans, L. (1997) Partial differential equations. American Mathematical Society, Providence.
- 20. 陈亚浙, 吴兰成 (1997) 二阶椭圆型方程与椭圆型方程组. 科学出版社, 北京.