Pure Mathematics
Vol.06 No.05(2016), Article ID:18558,7
pages
10.12677/PM.2016.65056
On Odd Deficient-Perfect Numbers with Four Distinct Prime Divisors
Lan Cui, Cong Zhang, Ying Li
Department of Mathematics and Finance, ABa Teachers University, Wenchuan Sichuan

Received: Sep. 1st, 2016; accepted: Sep. 15th, 2016; published: Sep. 20th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
For a positive integer n, let σ(n) denote the sum of the positive divisors of n. Let d be a proper divisor of n, we call n a deficient-perfect number if . On the basis of the references, we characterize some properties of odd deficient-perfect numbers with four distinct prime divisors. We prove that if
. On the basis of the references, we characterize some properties of odd deficient-perfect numbers with four distinct prime divisors. We prove that if  is an odd deficient-perfect number, then p1 = 3, p2 ≤ 13, and improve the result of the references.
is an odd deficient-perfect number, then p1 = 3, p2 ≤ 13, and improve the result of the references.
Keywords:Deficient-Perfect Numbers, The Sum of the Positive Divisors, Prime Factors, Order

具有四个素因子的奇亏完全数
崔兰,张聪,李颖
阿坝师范学院数学与财经系,四川 汶川

收稿日期:2016年9月1日;录用日期:2016年9月15日;发布日期:2016年9月20日

摘 要
设n为自然数,σ(n)表示n的所有正因子和函数。令d是n的真因子,若n满足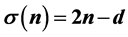 ,则称n为亏因子为d的亏完全数。在参考文献的基础上,本文讨论了具有四个素因子的奇亏完全数的一些性质,证明了
,则称n为亏因子为d的亏完全数。在参考文献的基础上,本文讨论了具有四个素因子的奇亏完全数的一些性质,证明了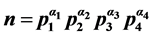 为具有四个不同素因子的奇亏完全数,则有p1 = 3, p2 ≤ 13。
为具有四个不同素因子的奇亏完全数,则有p1 = 3, p2 ≤ 13。
关键词 :亏完全数,因子和函数,素因子,阶

1. 引言与主要结果
对任意 ,设n的标准分解式为
,设n的标准分解式为 ,令ω(n),σ(n)分别表示n的相异素因子个数以及约数和函数,则
,令ω(n),σ(n)分别表示n的相异素因子个数以及约数和函数,则
 ,
, 。
。
约数和函数σ(n)是一类基本而又重要的数论函数,历史上许多著名数学难题都与它关 [1] [2] ,例如,著名的完全数问题。若正整数n满足σ(n) = 2n,则称n为完全数(perfect number)。若σ(n) < 2n,则称n为亏数(deficient),若σ(n) > 2n,则称n为过剩数(abundant)。设d是n的真因子,若 ,则称n为盈因子为d的盈完全数。如果
,则称n为盈因子为d的盈完全数。如果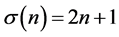 ,则称n为拟完全数(quasi-perfect)。若
,则称n为拟完全数(quasi-perfect)。若
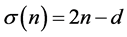 , (1)
, (1)
则称n为亏因子为d的亏完全数。特别地,如果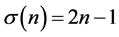 ,则称 为殆完全数(almost perfect),关于以上完全数的各类问题,以及σ(n)与Euler函数φ(n)的迭代等等问题,可参见文献 [3] - [16] 。
,则称 为殆完全数(almost perfect),关于以上完全数的各类问题,以及σ(n)与Euler函数φ(n)的迭代等等问题,可参见文献 [3] - [16] 。
关于亏完全数,文献 [17] 刻画了素因子个数不超过2的所有亏完全数的结构,若n为亏完全数且ω(n) ≤ 2,则
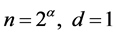
或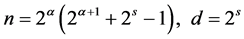 ,
,
其中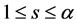 ,且
,且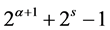 为奇素数。文献 [18] 证明不存在具有三个素因子的奇亏完全数。最近,文献 [19] 研究具有四个素因子的奇亏完全数,证明了若
为奇素数。文献 [18] 证明不存在具有三个素因子的奇亏完全数。最近,文献 [19] 研究具有四个素因子的奇亏完全数,证明了若 为具有四个不同素因子的奇亏完全数,其中
为具有四个不同素因子的奇亏完全数,其中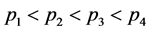 为奇素数,则有
为奇素数,则有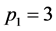 ,且
,且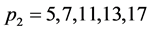 。
。
在文献 [19] 的基础上,本文进一步研究具有四个素因子的奇亏完全数,略微改进了文献 [19] 中的结论,证明了
定理 若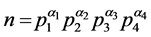 为具有四个不同素因子的奇亏完全数,则有
为具有四个不同素因子的奇亏完全数,则有
 。
。
2. 一些引理
引理1 若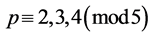 ,则
,则 ,若
,若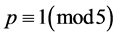 ,则
,则
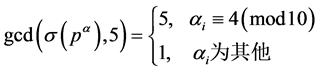
证明:若 ,则
,则
 。
。
同理可得,若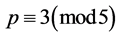 ,则
,则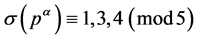 ,若
,若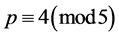 ,则
,则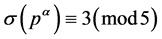 。若
。若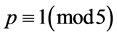 ,则
,则 。
。
引理2 若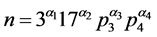 是奇亏完全数时,亏因子
是奇亏完全数时,亏因子 ,其中
,其中 ,
,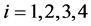 ,令
,令
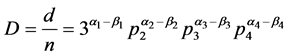 ,
,
则 均为偶数,且
均为偶数,且
 。 (2)
。 (2)
证明:由于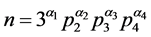 为奇亏完全数,则由(1)可得,
为奇亏完全数,则由(1)可得,
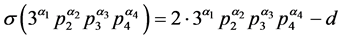 (3)
(3)
其中
 ,
,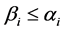 ,
,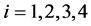 。
。
则
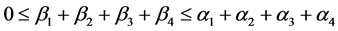 。
。
由于d为奇数,则根据(3)式,有
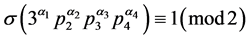
因此
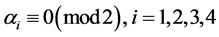 ,
,
则根据(1)式,有
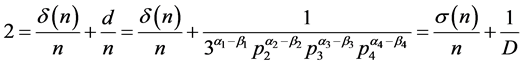 (4)
(4)
当 ,
,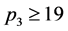 时,若
时,若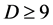 ,则
,则
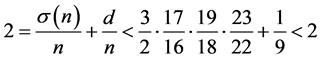
矛盾,则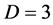 。
。
引理3 若 是奇亏完全数,
是奇亏完全数,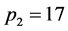 ,则
,则
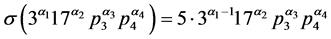 (5)
(5)
证明:由引理2知,当 时,
时, ,则
,则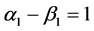 和
和 ,
,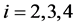 ,由(3)式可得
,由(3)式可得
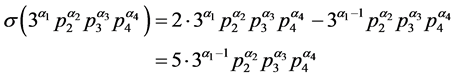 。
。
引理4 令
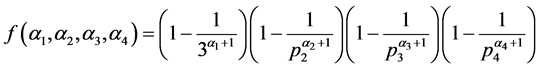 ,
,
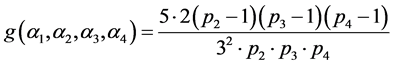 ,
,
则
 。 (6)
。 (6)
证明:由引理3知
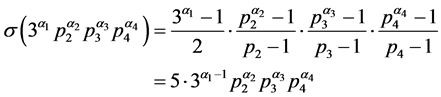
所以

则(6)式成立。
3. 主要结果的证明
设m > 2为正整数,a为整数,若(a,m) = 1,称满足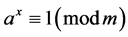 的最小正整数x为a对模m的阶,记作ordma。
的最小正整数x为a对模m的阶,记作ordma。
若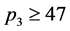 时,则
时,则
 ,
,
矛盾,因此,
 。
。
情形1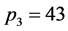 。当
。当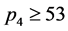 时,
时,
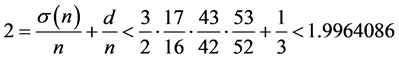 ,
,
矛盾,因此 。由于ord35 = 4,如果
。由于ord35 = 4,如果 ,则
,则
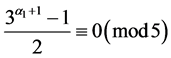 ,
,
则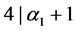 ,矛盾,因此
,矛盾,因此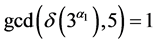 。同理,由于
。同理,由于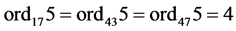 ,则
,则
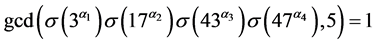 ,
,
这与(5)式矛盾。
情形2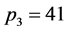 。当
。当 时
时
 ,
,
矛盾,因此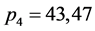
当 时,计算
时,计算 和
和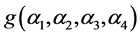 的值如下,
的值如下,
由引理4得,与(6)式矛盾。当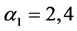 时,
时,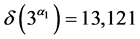 ,与(5)式矛盾。
,与(5)式矛盾。
情形3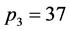 。当
。当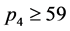 时
时
 ,
,
矛盾,因此, 。由于
。由于 ,则
,则
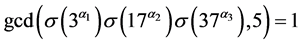 。
。
由引理1知,要使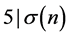 则必使
则必使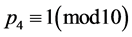 ,所以
,所以 。当
。当 ,且
,且 时,有
时,有
 ,
,
 ,
,
与(6)式矛盾。若 ,
,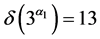 ,与(5)式矛盾。
,与(5)式矛盾。
情形4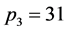 。当
。当 时
时
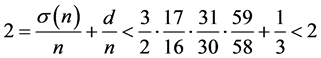
矛盾,因此,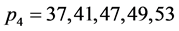 。
。
当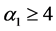 时,计算
时,计算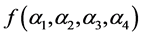 和
和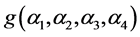 的值如下,
的值如下,
由引理4得,与(6)式矛盾。当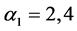 时,
时, ,与(5)式矛盾。
,与(5)式矛盾。
情形5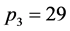 ,当
,当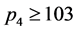 时,有
时,有
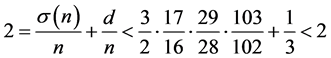 ,
,
矛盾,则 。由于
。由于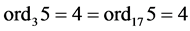 ,ord295 = 2,由引理1知,若要使
,ord295 = 2,由引理1知,若要使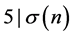 ,则必须使
,则必须使 ,所以
,所以
当 ,且
,且 时,当
时,当 ,且
,且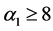 时,分别计算
时,分别计算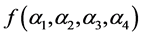 和
和 的值如下:
的值如下:
由引理4得,与(6)式矛盾。
当 时,
时, ,与(5)式矛盾。
,与(5)式矛盾。
情形6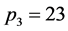 ,当
,当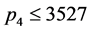 时,有
时,有
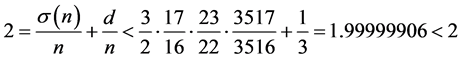 ,
,
矛盾,则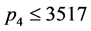 。由于
。由于 ,同理由引理1知,使
,同理由引理1知,使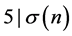 则必使
则必使 ,所以
,所以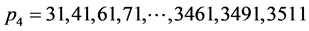 。
。
当 ,
, ,
,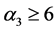 时,由于
时,由于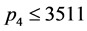 ,则有
,则有
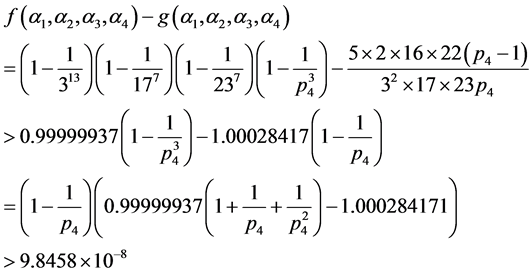 。
。
由引理4得,与(6)式矛盾。
当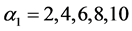 ,
,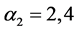 ,以及
,以及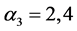 时,
时,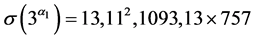 ,
, ,
,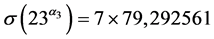 ,与(5)式均为矛盾。
,与(5)式均为矛盾。
情形7: 。当
。当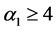 时,由于
时,由于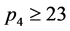 ,则有
,则有
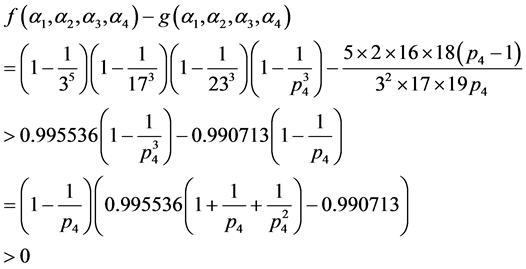 。
。
由引理4得,与(6)式矛盾。
当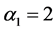 时,
时,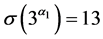 ,与(5)式矛盾。
,与(5)式矛盾。
因此,定理得证。
基金项目
阿坝师范学院科研课题项目(JXYY201507),四川省教育厅自然科学研究项目(15ZA0337)。
致谢
作者衷心感谢阿坝师范学院杨仕椿教授的悉心指导和热情帮助!
文章引用
崔 兰,张 聪,李 颖. 具有四个素因子的奇亏完全数
On Odd Deficient-Perfect Numbers with Four Distinct Prime Divisors[J]. 理论数学, 2016, 06(05): 411-417. http://dx.doi.org/10.12677/PM.2016.65056
参考文献 (References)
- 1. Guy, R.K. (1981) Unsolved Problems in Number Theory. Springer-Verlag, New York, 25-56. http://dx.doi.org/10.1007/978-1-4757-1738-9
- 2. 华罗庚. 数论导引[M]. 北京: 科学出版社, 1979: 13-14.
- 3. Erdos, P. (1959) Remarks on Number Theory II: Some Problems on the σ Function. Acta Arithmetica, 5, 171-177.
- 4. Poliack, P. and Shevelev, P. (2012) On Perfect and Near-Perfect Numbers. Journal of Number Theory, 132, 3037-3046. http://dx.doi.org/10.1016/j.jnt.2012.06.008
- 5. Abbott, H.L., Aull, C.E., Brown, E., et al. (1973) Quasi Perfect Numbers. Acta Arithmetica, 22, 439-447.
- 6. Cattaneo, P. (1951) Sui Numeriquasi Perfetti. Boll.Un. Mat. Ital., 6, 59-62.
- 7. Pomerance, C. (1975) On the Congrunces σ(n) ≡ a (mod n) and n ≡ a (mod ϕ(n)). Acta Arithmetica, 26, 265-272.
- 8. Kishore, M. (1978) Odd Integers n with Five Distinct Prime Factors for Which 2-10−12<σ(n)/n< 2+10−12. Mathematics of Computation, 32, 303-309. http://dx.doi.org/10.2307/2006281
- 9. Cohen, G.L. (1980) On Odd Perfect Numbers. II. Multiperfect Numbers and Quasiperfect Numbers. Journal of the Australian Mathematical Society Series A, 29, 369-384. http://dx.doi.org/10.1017/S1446788700021376
- 10. Kishore, M. (1981) On Odd Perfect, Quasiperfect, and Odd Almost Perfect Numbers. Mathematics of Computation, 36, 583-586. http://dx.doi.org/10.1090/S0025-5718-1981-0606516-3
- 11. Cohen, G.L. (1982) The Nonexistence of Quasiperfect Numbers of Certain Forms. The Fibonacci Quarterly, 20, 81-84.
- 12. Hagis, P. and Cohen, G.L. (1982) Some Results Concerning Quasiperfect Numbers. Journal of the Australian Mathematical Society Series A, 33, 275-286. http://dx.doi.org/10.1017/S1446788700018401
- 13. Tang, M. and Li, M. (2012) On the Congruence σ(n) ≡ 1 (mod n). Journal of Mathematical Research with Applications, 32, 673-676.
- 14. Anavi, A., Pollack, P. and Pomerance, C. (2013) On Congrunces of the Form σ(n) ≡ a (mod n). International Journal of Number Theory, 9, 115-124. http://dx.doi.org/10.1142/S1793042112501266
- 15. Li, M. and Tang, M. (2014) On the Congruence σ(n) ≡ 1 (mod n) II. Journal of Mathematical Research with Applications, 34, 155-160.
- 16. Tang, M. and Feng, M. (2014) On Deficient-Perfect Numbers. Bulletin of the Australian Mathematical Society, 90, 186-194. http://dx.doi.org/10.1017/S0004972714000082
- 17. Ren, X.Z. and Chen, Y.G. (2013) On Near-Perfect Numbers with Two Distinct Prime Factors. Bulletin of the Australian Mathematical Society, 88, 520-524. http://dx.doi.org/10.1017/S0004972713000178
- 18. Tang, M., Ren, X.Z. and Li, M. (2013) On Near-Perfect and Deficient-Perfect Numbers. Colloquium Mathematicum, 133, 221-226. http://dx.doi.org/10.4064/cm133-2-8
- 19. 马小艳, 王玉杰. 具有四个素因子的奇亏完全数[J]. 纯粹数学与应用数学, 2015, 31(6): 643-649.