Pure Mathematics
Vol.07 No.04(2017), Article ID:21229,5
pages
10.12677/PM.2017.74030
A New Geometrical Representation over Quaternion Field
Wenye Wang, Dezhong Lian, Wencheng Wu
Department of Information Engineering Institute, Longyan University, Longyan Fujian

Received: Jun. 15th, 2017; accepted: Jun. 29th, 2017; published: Jul. 3rd, 2017

ABSTRACT
By using several geometrical characteristics of similar class of quaternion, this paper separates the quaternion field into a direct product between a half of complex field and whole surface of a unit sphere on virtual vector space. This is an effective method to discuss the similar properties of functions between complex field and quaternion field.
Keywords:Quaternion, Quaternion Field, Similar Quaternion Numbers, Similar Class, Geometric Representation
四元数体的几何表示
王文烨,连德忠,吴文城
福建龙岩学院信息工程学院,福建 龙岩
收稿日期:2017年6月15日;录用日期:2017年6月29日;发布日期:2017年7月3日

摘 要
本文利用四元数相似类的几何特征,将四元数体分解为平面与虚部向量空间单位球面的直积,为进一步探讨四元数函数与复函数的相似关系提供了一条有效途径。
关键词 :四元数,四元数体,相似四元数,相似类,几何表示

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
从二十世纪六、七十年代开始,随着控制理论、陀螺技术和计算技术的发展,四元数的研究得到学术界的普遍重视 [1] 。近二、三十年来,国内不少专家学者对四元数理论进行了广泛的研究,取得了相当丰硕的科研成果 [2] [3] [4] [5] 。在这些科研成果中,与四元数代数理论相关的科研成就比较突出,而在四元数分析理论方面所取得的进展则逊色些。四元数分析理论进展不顺的主要原因就是受柯西–黎曼条件限制,大多数初等四元数函数都不解析(如四元数函数 不解析)。为了打破僵局,本文利用四元数相似类的几何特征,将四元数体分解为平面与虚部向量空间单位球面的直积,为进一步探讨四元数函数与复函数的相似关系提供了一条有效途径。
不解析)。为了打破僵局,本文利用四元数相似类的几何特征,将四元数体分解为平面与虚部向量空间单位球面的直积,为进一步探讨四元数函数与复函数的相似关系提供了一条有效途径。
2. 四元数的相似定义和基本性质
设 —实数域,
—实数域, —复数域,
—复数域, —实四元数体。
—实四元数体。
定义1.1 [1] 对于四元数 、
、 ,若存在非零四元数
,若存在非零四元数 ,满足
,满足 ,则称
,则称 与
与 相似,并记
相似,并记
四元数的相似具有以下性质:自反性(每个四元数与自身相似);对称性(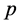 与
与 相似,则
相似,则 与
与 也相似);传递性(
也相似);传递性( 与
与 相似,
相似,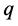 与
与 相似,则
相似,则 与
与 相似)。
相似)。
由于实数与四元数的乘积可交换顺序,因此实数只与自身相似。
引理1.1 [2] 对于任意一个非实四元数 (
(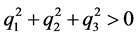 ),
), 与复数
与复数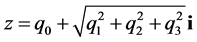 相似。
相似。
引理1.2对于任意一组相似四元数 与
与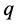 ,
,
即非零四元数 可单位化(这里
可单位化(这里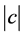 代表四元数
代表四元数 的模 [2] ,证明略)
的模 [2] ,证明略)
引理1.3 [2] 对于任意四元数 、
、 ,
,
记 (
( 的实部),
的实部), ,
,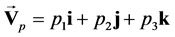 (
(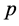 的虚部向量),
的虚部向量),
 ,那么
,那么
即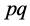 的实部=
的实部= ,
, 的虚部=
的虚部= 
引理1.4对于任意四元数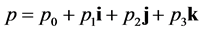 、
、 ,
,
 与
与 相似
相似
 ,且
,且
(这里 、
、 分别代表
分别代表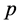 、
、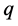 的模 [2] )
的模 [2] )
证明:如果 与
与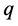 相似,那么存在非零单位四元数
相似,那么存在非零单位四元数 ,满足
,满足

而 为非零单位四元数,故
为非零单位四元数,故 ,根据引理1.3
,根据引理1.3
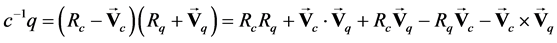

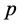 的实部
的实部
上式中的 是一个向量混合积,结果为零,
是一个向量混合积,结果为零,
故 ,即
,即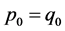 。
。
反之,如果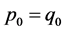 且
且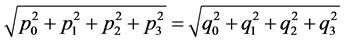 ,那么
,那么
 ,根据引理1.1,
,根据引理1.1, 和
和 都与复数
都与复数 相似,由四元数相似的传递性和对称性可知,
相似,由四元数相似的传递性和对称性可知, 与
与 相似。
相似。
3. 四元数体的几何表示
定义2.1 [2] 对于任意 ,记集合
,记集合 ,称
,称 为
为 的相似类
的相似类
很明显,实数的相似类只有一个元素,就是该实数本身。
引理2.1 [2] 对于任意一个四元数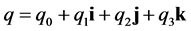 ,只要
,只要
那么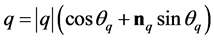 ,其中,
,其中, 为
为 的幅角,
的幅角, 为
为 的单位方向矢量。
的单位方向矢量。
对于任意一个非实四元数 (
( ),
),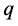 由
由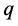 的模
的模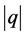 、
、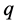 的幅角
的幅角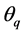 、
、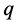 的单位方向矢量
的单位方向矢量 唯一确定。根据引理1.4,所有与
唯一确定。根据引理1.4,所有与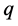 具有相同的模和实部,但单位方向矢量与
具有相同的模和实部,但单位方向矢量与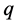 不同的四元数都与
不同的四元数都与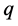 相似。因此,所有与
相似。因此,所有与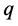 相似的四元数的单位方向矢量构成四元数虚部向量空间一个以单位长度为半径的球面(如图1所示),也就是说
相似的四元数的单位方向矢量构成四元数虚部向量空间一个以单位长度为半径的球面(如图1所示),也就是说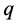 的相似类
的相似类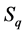 中的所有元素的单位方向矢量构成四元数虚部向量空间一个单位球面。而
中的所有元素的单位方向矢量构成四元数虚部向量空间一个单位球面。而 中所有元素相同的模
中所有元素相同的模 和幅角
和幅角 (
( )对应复平面上半部分中的一点,该点的极坐标就是
)对应复平面上半部分中的一点,该点的极坐标就是 (如图2所示);
(如图2所示);

Figure 1. The imaginary part unit sphere surface over quaternion field
图1. 四元数虚部单位球面

Figure 2. The modulus and angles of quaternion
图2. 四元数的模和幅角
在 中有一对共轭复数
中有一对共轭复数 ,这一对共轭复数在的单位方向矢量分别为
,这一对共轭复数在的单位方向矢量分别为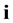 和
和 ;而复数
;而复数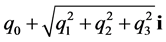 在复平面上投影点的极坐标也是
在复平面上投影点的极坐标也是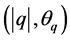 ,因此,将复数
,因此,将复数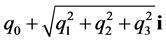 定义为四元数
定义为四元数 的相似类
的相似类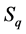 的主值。
的主值。
四元数体上的全体四元数如果按相似类分类,其几何特征非常直观。每个四元数相似类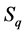 对应四元数虚部向量空间一个单位球面,又对应复平面上半部分的一点,该点的极坐标就是
对应四元数虚部向量空间一个单位球面,又对应复平面上半部分的一点,该点的极坐标就是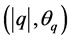 (注:
(注: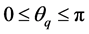 )。四元数体上全体四元数相似类在复平面上的投影点构成复平面上半平面。也就是说:四元数体
)。四元数体上全体四元数相似类在复平面上的投影点构成复平面上半平面。也就是说:四元数体 上的每个非实四元数分别可以在复平面上半部分和四元数虚部向量空间单位球面上拥有一个投影点,在上半平面投影点的极坐标就是该元素的模和幅角,在虚部向量空间单位球面上的投影点就是该元素单位方向矢量的顶点。
上的每个非实四元数分别可以在复平面上半部分和四元数虚部向量空间单位球面上拥有一个投影点,在上半平面投影点的极坐标就是该元素的模和幅角,在虚部向量空间单位球面上的投影点就是该元素单位方向矢量的顶点。
四元数体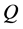 中的非实复数
中的非实复数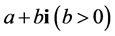 可以这样表示
可以这样表示

因此复数 在复平面上投影点的极坐标为
在复平面上投影点的极坐标为
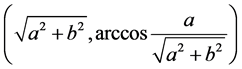 ,在虚部向量空间单位球面上的投影点就是
,在虚部向量空间单位球面上的投影点就是 的顶点;
的顶点;
而复数 的共轭复数
的共轭复数 可以这样表示
可以这样表示

因此复数 在平面投影点的极坐标也为
在平面投影点的极坐标也为
 ,在虚部向量空间单位球面上的投影点就是
,在虚部向量空间单位球面上的投影点就是 的顶点。
的顶点。
四元数体 中的非负实数
中的非负实数 可以这样表示
可以这样表示
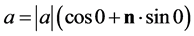 (为四元数虚部向量空间中的任意一个单位方向矢量)
(为四元数虚部向量空间中的任意一个单位方向矢量)
负实数 可以这样表示
可以这样表示
 (为四元数虚部向量空间中的任意一个单位方向矢量)
(为四元数虚部向量空间中的任意一个单位方向矢量)
因此,实数在复平面上的投影点落在极轴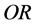 或
或 的反向延长线上,而虚部向量空间单位球面上每
的反向延长线上,而虚部向量空间单位球面上每
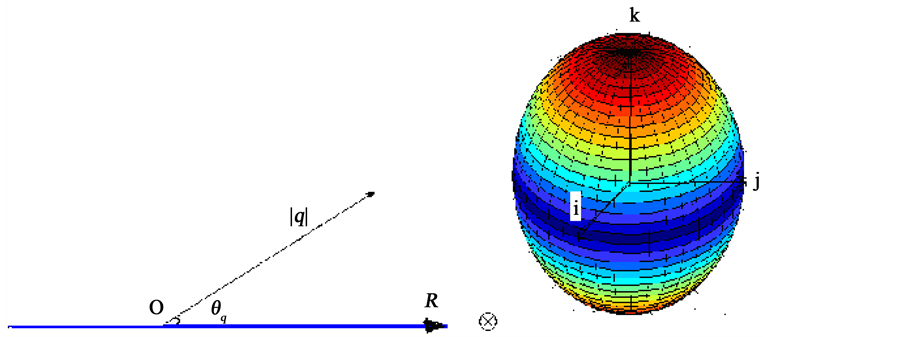
Figure 3. The geometric representation of quaternion field
图3. 四元数体的几何表示
个点都可以作为实数的投影点,为此,我们约定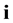 的顶点作为实数在虚部向量空间单位球面上的投影点,这样实数和非实复数
的顶点作为实数在虚部向量空间单位球面上的投影点,这样实数和非实复数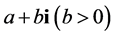 在虚部向量空间单位球面上拥有相同的投影点,那就是
在虚部向量空间单位球面上拥有相同的投影点,那就是 的顶点。
的顶点。
综上所述,四元数体 按相似类可以表示为复平面上半部分(包括极轴
按相似类可以表示为复平面上半部分(包括极轴 和
和 的反向延长线)与四元数虚部向量空间单位球面的直积。任意一个四元数
的反向延长线)与四元数虚部向量空间单位球面的直积。任意一个四元数 在复平面上投影点的直角坐标为
在复平面上投影点的直角坐标为 ,在虚部向量空间单位球面上的投影点是单位方向矢量
,在虚部向量空间单位球面上的投影点是单位方向矢量 的顶点(图3)。
的顶点(图3)。
项目资助
本文由福建省大学生创新创业训练计划项目(S20141005)资助。
文章引用
王文烨,连德忠,吴文城. 四元数体的几何表示
A New Geometrical Representation over Quaternion Field[J]. 理论数学, 2017, 07(04): 236-240. http://dx.doi.org/10.12677/PM.2017.74030
参考文献 (References)
- 1. [前苏联] B.H.勃拉涅茨, Й.П.什梅格列夫斯基. 四元数在刚体定位问题中的应用[M]. 梁振和, 译, 汪朝群, 校. 北京: 国防工业出版社, 1977: 23-28.
- 2. 李文亮. 四元数矩阵[M]. 长沙: 国防科技大学出版社, 2002: 6-21.
- 3. 陈龙玄. 四元数矩阵的特征值和特征向量[J]. 烟台大学学报, 1993, 10(3): 1-8.
- 4. 王秋媛. 四元数的解析性[J]. 北京交通大学学报, 2000, 24(2): 23-26.
- 5. 姜同松. 四元数的一种新的代数结构[J]. 力学学报, 2002, 34(1): 116-122.