Pure Mathematics
Vol.07 No.05(2017), Article ID:21950,8
pages
10.12677/PM.2017.75049
Travelling Wave Solution of the Generalized KDV Equation
Xiaojiao Wang*, Xianlin Zhou, Fangqi Wei
College of Mathematics and Software Science, Sichuan Normal University, Chengdu Sichuan
*通讯作者。

Received: Aug. 17th, 2017; accepted: Aug. 31st, 2017; published: Sep. 6th, 2017

ABSTRACT
By combining the fractional transform with Cn-expansion method, we give the improved elliptic expansion method to solve the generalized fraction KDV equations, and obtain some new periodic solution and solitary wave solutions.
Keywords:Complex-Transform-Cn Expansion Method, Modified Riemann-Liouville Derivative, Fractional Generalized KDV Equation
分数阶广义KDV方程的精确解
王小娇*,周贤林,韦方棋
四川师范大学数学与软件科学学院,四川 成都

收稿日期:2017年8月17日;录用日期:2017年8月31日;发布日期:2017年9月6日

摘 要
本文将分数阶复变换方法和椭圆函数展开法相结合,给出了求解分数阶广义KDV方程的复变换椭圆函数展开法。进而得到了分数阶广义KDV方程的周期波解和孤立波解。
关键词 :复变换椭圆函数展开法,修正Riemann-Liouville函数,分数阶广义KDV方程

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
自然科学中的定律及原理是用偏微分方程来表达的,因而偏微分方程是联结数学与自然科学的关键性纽带,求解偏微分方程的显示解,特别是行波解,在理论和实际中有重要的作用,并受到数学和物理学家的广泛关注。许多数学工具和方法被用来求解非线性偏微分方程的行波解。如反散色法 [1] ,Backlund法 [2] ,Darboux变换法 [3] ,Hirota双线性法 [4] ,延拓法 [5] ,Painleve分析法 [6] ,有限差分法 [7] ,Tanh法 [8] 和Sin-Cos法 [9] ,首次积分法 [10] ,试探函数法 [11] 等。由于非线性偏微分方程形式和特征的多样性,尚无一种适用于求解所有类型偏微分方程的方法。
本文研究如下广义KDV方程的行波解
 (1)
(1)
其中,分数阶微分算子 是Jumarie的修正Riemann-Liouville导数 [12] ,其定义如下:
是Jumarie的修正Riemann-Liouville导数 [12] ,其定义如下:
 (2)
(2)
 为Gamma函数,定义为:
为Gamma函数,定义为:
 (3)
(3)
Jumarie的修正Riemann-Liouville导数有如下性质:
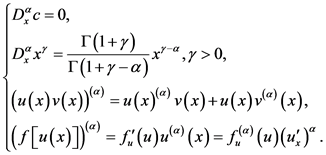 (4)
(4)
显然,方程(1)为一类典型的非线性偏微分方程。分数阶非线性偏微分方程是整数阶非线性偏微分方程的自然推广,可以解释许多整数阶非线性偏微分方程无法解释的现象,因而得到了生物、化学、物理、数学等领域学者的广泛关注和高度重视。现已广泛运用到流体力学 [13] 、生物医学 [14] 、固态物理 [15] 等工程领域,并对这些领域的发展产生了深远的影响。寻求分数阶微分方程的精确解已成了数学工作者的重要研究课题,得到了一些求解分数阶非线性方程的方法。如分数阶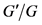 展开法 [16] ,分数阶子方程法 [17] ,分数阶微分变换法 [18] ,分数阶同伦扰动法 [19] 等。
展开法 [16] ,分数阶子方程法 [17] ,分数阶微分变换法 [18] ,分数阶同伦扰动法 [19] 等。
最近,Li Zheng Biao和He Ji Huan等人提出了分数阶复变换法 [20] ,运用该方法可将分数阶偏微分方程转化为整数阶偏微分方程。本文将分数阶复变换法与Cn函数展开法 [21] 相结合,求解了分数阶广义的KDV方程(1)。最终,我们获得了方程(1)的周期解和孤立波解,当分数阶导数 时,所得到的精确解就是通常的行波解,大大丰富了此方程的解系,为专家学者在某些问题的研究上提供了帮助。
时,所得到的精确解就是通常的行波解,大大丰富了此方程的解系,为专家学者在某些问题的研究上提供了帮助。
2. 复变换-Cn函数展开法
基于复变换方法和Cn函数展开法,得到下面的复变换-Cn函数展开法,该方法主要步骤如下:
第一步,考虑如下分数阶微分方程:
 (5)
(5)
其中 是代数函数
是代数函数 关于自变量t和x的Jumarie的修正Riemann-Liouville导数,P是关于函数u及偏导数的多项式,P中含有最高阶导数和非线性项。
关于自变量t和x的Jumarie的修正Riemann-Liouville导数,P是关于函数u及偏导数的多项式,P中含有最高阶导数和非线性项。
作分数阶复变换:
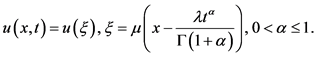 (6)
(6)
其中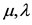 是常数,当
是常数,当 时,式(6)就是通常的行波变换,在式(6)的作用下,式(5)变为:
时,式(6)就是通常的行波变换,在式(6)的作用下,式(5)变为:
 (7)
(7)
第二步,假设(7)式的解u可以表示为C的多项式形式:
 (8)
(8)
其中 是待定常数,
是待定常数, 。正整数K通过式(7)中的最高阶导数项和非线性项来确定。
。正整数K通过式(7)中的最高阶导数项和非线性项来确定。
记 ,由椭圆函数的导数公式有:
,由椭圆函数的导数公式有:
 (9)
(9)
若以 表示u的最高幂次的次数K,则
表示u的最高幂次的次数K,则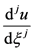 最高幂次的次数应为:
最高幂次的次数应为:
 (10)
(10)
而 的最高幂次的系数为
的最高幂次的系数为
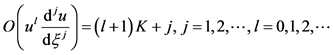 (11)
(11)
将(8)式代入(7)式,平衡方程(7)中的最高阶导数项和非线性项的幂次,可以确定参数K的值,同时利用(9)式等可以导出代数方程
 (12)
(12)
其中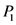 和
和 为C的多项式,令
为C的多项式,令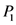 和
和 中C的各幂次系数为零,便得到确定
中C的各幂次系数为零,便得到确定 及
及 和
和 的代数方程组。运用Wu消元法求解这个代数方程组,就得到(5)式的形如(8)的周期波解。特别地,令模数
的代数方程组。运用Wu消元法求解这个代数方程组,就得到(5)式的形如(8)的周期波解。特别地,令模数 ,就可以得到相应的孤立波解。
,就可以得到相应的孤立波解。
3. 分数阶广义KDV方程
考虑如下分数阶广义KDV方程:
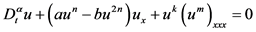 (13)
(13)
对(13)式作复变换:
 (14)
(14)
经过整理变形,方程(14)化为
 (15)
(15)
假设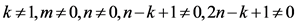 。对方程(15)积分,并忽略积分常数,得到关于
。对方程(15)积分,并忽略积分常数,得到关于 的二阶常微分方程
的二阶常微分方程
 (16)
(16)
平衡式(16)中的最高阶导数项和非线性项得到
 (17)
(17)
所以
 (18)
(18)
情况3.1 当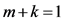 时,方程(16)化为
时,方程(16)化为
 (19)
(19)
令 ,代入到(19)中得到
,代入到(19)中得到
 (20)
(20)
假设式(20)具有如下形式解
 (21)
(21)
平衡式(20)中最高阶导数项和非线性项得到K = 1,将(21)代入式(20),其中
 (22)
(22)
合并C相同幂次,并令每一项系数为零,得到一组关于 的方程组
的方程组
 (23)
(23)
借助Wu消元法求解方程组得到
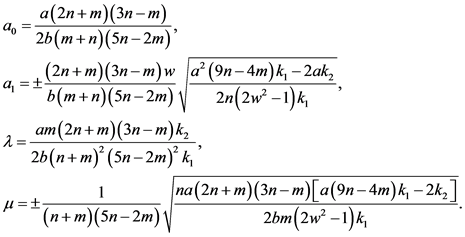 (24)
(24)
其中
 (25)
(25)
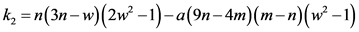 (26)
(26)
于是
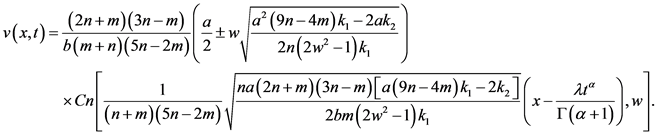 (27)
(27)
特别的,当 时
时
 (28)
(28)
其中 ,
, 的值由上给出,因此得到广义KDV方程精确解如下:
的值由上给出,因此得到广义KDV方程精确解如下:
 (29)
(29)
 (30)
(30)
情况3.2当 时,方程(16)化为
时,方程(16)化为
 (31)
(31)
令 ,代入到(31)得到
,代入到(31)得到
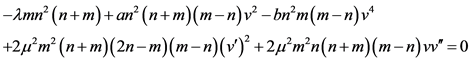 (32)
(32)
假设式(31)具有如下形式解
 (33)
(33)
平衡式(32)中最高阶导数项和非线性项得到K=1,将(33)代入式(32),合并C的相同幂次,并令每一项系数为零,得到一组关于 的方程组
的方程组
 (34)
(34)
借助Wu消元法求解方程组得到
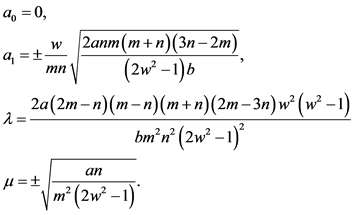 (35)
(35)
于是
 (36)
(36)
特别的,当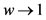 时
时
 (37)
(37)
其中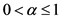 ,
, 的值由上给出.因此得到广义KDV方程精确解如下:
的值由上给出.因此得到广义KDV方程精确解如下:
 (38)
(38)
 (39)
(39)
4. 结语
将分数阶复变换方法和Cn函数展开法相结合,得到了求解分数阶非线性方程的精确解的一种新方法。本文求解了广义KDV方程,得到了此方程的新的精确解。当分数阶导数 时,所得到的精确解就是通常的行波解。
时,所得到的精确解就是通常的行波解。
基金项目
四川省杰出青年基金(2014JQ0039),国家自然科学基金(11501395)。
文章引用
王小娇,周贤林,韦方棋. 分数阶广义KDV方程的精确解
Travelling Wave Solution of the Generalized KDV Equation[J]. 理论数学, 2017, 07(05): 378-385. http://dx.doi.org/10.12677/PM.2017.75049
参考文献 (References)
- 1. Rosenau, P. (1997) On Nonanalytic Solitary Waves Formed by a Nonlinear Dispersion. Physical Letters A, 230, 305-318. https://doi.org/10.1016/S0375-9601(97)00241-7
- 2. Lai, S.Y. and Yin, Q. (2001) A New Study for the Modified Nonlinear Dispersive mK(m,n)Equations in Higher Dimensional Spaces. Journal of Pure and Applied Mathematical Science in China(Series A), 44, 396-401.
- 3. Pelinovsky, D. and Grimshaw, R. (1996) An Asymptotic Approach to Solitary Wave Instability and Critical Collapse in Long-Wave KdV-Type Evolution Equations. Physica D, 98, 139-155. https://doi.org/10.1016/0167-2789(96)00093-0
- 4. Klaus, M., Pelinovsky, D. and Rothos, V. (2006) Evans Function for Lax Operators with Algebraically Decaying Potentials. Journal of Nonlinear Science, 16, 1-44. https://doi.org/10.1007/s00332-005-0652-7
- 5. Pelinovsky, D., Afanasjev, V. and Kivshar, V. (1996) Nonlinear Theory of Oscillating, Decaying and Collapsing Solitions in the Generalized Nonlinear Schrodinger Equation. Physical Review E, 53, 1940-1953. https://doi.org/10.1103/PhysRevE.53.1940
- 6. Wazwaz, A.M. (2006) Compactons and Soltary Wave Solutions for the Bousinesq Wave Equation and Its Generalized Form. Applied Mathematics Computation, 182, 529-535. https://doi.org/10.1016/j.amc.2006.04.014
- 7. Wazwaz, A.M. (2006) The Sine-Cosine and the Tanh Methods: Reliable Tools for Analytic Treatment of Nonlinear Dispersive Equations. Applied Mathematics Computation, 173, 150-164. https://doi.org/10.1016/j.amc.2005.02.047
- 8. Wazwaz, A.M. (2005) Nonlinear Variants of the Improved Boussinesq Equation with Compact and Noncompact Structures. Applied Mathematics Computation, 49, 565-574. https://doi.org/10.1016/j.camwa.2004.07.016
- 9. Wazwaz, A.M. (2006) Kinks and Solitons Solutions for the Generalized KdV Equation with Two Power Nonlinearities. Applied Mathematics Computation, 183, 1181-1189. https://doi.org/10.1016/j.amc.2006.06.042
- 10. Wazwaz, A.M. (2001) A Study of Nonlinear Dispersive Equations with Solitary-Wave Solutions Having Compact Support. Mathematics and Computers in Simulation, 56, 269-276. https://doi.org/10.1016/S0378-4754(01)00291-9
- 11. Ismail, M.S. and Taha, T.R. (1998) A Numerical Study of Compactons. Mathematics and Computers in Simulation, No. 47, 519-530.
- 12. Jumarie, G. (2006) Modified Riemann-Liouville Derivative and Fractional Taylor Series of Non-Differentiable Functions Further Results. Computers and Mathematics with Applications, 51, 1367-1376.
- 13. Sabatier, J., Agrawal, O.P. and Tenreiro Machado, J.A. (2007) Advances in Fractional Calculus: Theoretical Develop¬ments and Applications in Physics and Engineering. Springer, 50, 1648-1650.
- 14. Baleanu, D., Diethelm, K., Scalas, E., et al. (2012) Fractional Calculus Models and Numerical Methods in Series on Complexity, Monlinearity and Chaos. World Scientific, Singapore, 216, 67-75.
- 15. Liu, Y.Q. and Xin, B.G. (2011) Numerical Solutions of a Fractional Predator-Prey System. Advances in Difference Equations, 51, 1159-1162.
- 16. Wang, M.L., Li, X.Z. and Zhang, J.L. (2008) The G/G-Expansion Method and Travelling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics. Physics Letters A, 37, 417-423.
- 17. Liu, Y.Q. and Yan, L.M. (2013) Solutions of Fractional Konopelchenko-Dubrovsky and Nizhnik-Novikov-Veselov Equations using a Generalized Fractional Sub-Equation Method. Abstract and Applied Analysis, 11, 515-521.
- 18. Khan, N.A., Ara, A. and Mahmood, A. (2012) Numerical Solutions of Time Fractional Burgers Equations: A Compar¬ison between Generalized Differential Transformation Technique and Homotopy Perturbation Methon. International Journal of Numerical Methods for Heat and Fluid Flow, 24, 175-193. https://doi.org/10.1108/09615531211199818
- 19. He, J.H. (2003) Homotopy Perturbation Method: A New Nonlinear Analytical Technique. Applied Mathematics and Computation, 135, 73-79.
- 20. Li, Z.B. and He, J.H. (2010) Fractional Complex Transform for Fractional Differential Equations. Mathematical and Computational Applications, 15, 970-973. https://doi.org/10.3390/mca15050970
- 21. 刘式达, 傅遵涛. 一类非线性方程的新周期解[J]. 物理学报, 2002, 51(1): 10-14.