Pure Mathematics
Vol.08 No.02(2018), Article ID:24034,13
pages
10.12677/PM.2018.82018
Multiple Change-Points Detection of Piecewise Stationary Time Series
Nan Wu1, Yao Hu1,2*, Dan Wang1
1School of Mathematics and Statistics, Guizhou University, Guiyang Guizhou
2Guizhou Provincial Key Laboratory of Public Big Data, Guiyang Guizhou

Received: Feb. 23rd, 2018; accepted: Mar. 9th, 2018; published: Mar. 14th, 2018

ABSTRACT
The change-point problem has a wide range of applications in the industrial, financial, meteorology and other fields. A method for estimating the numbers, locations of change-point by building the Likelihood ratio scan (LRS) statistics, combined with the Minimum description length (MDL) principle has been proposed. It reduces the computationally infeasible global multiple-change-point estimation problem to a number of single-change-point detection problems in various local windows by effective segmentation. In order to provide more information for describing change points, we have constructed confidence intervals for each of the change points. Finally, extensive simulation studies and example analysis of traffic show the LRS usability practice.
Keywords:Multiple Change-Points, Likelihood Ratio, Confidence Intervals, Minimum Description Length Criterion
分段平稳时间序列中的多变点检测
吴楠1,胡尧1,2*,王丹1
1贵州大学数学与统计学院,贵州 贵阳
2贵州省公共大数据重点实验室,贵州 贵阳

收稿日期:2018年2月23日;录用日期:2018年3月9日;发布日期:2018年3月14日

摘 要
变点问题在工业、金融、气象等领域有着广泛的应用。针对分段平稳时间序列的多变点检测,提出一种通过构建似然比扫描(LRS)统计量,结合最小描述长度(MDL)准则对变点数量、位置进行估计的方法,将计算上不可行的全局多变点估计问题通过有效分段降为各局部窗口中的多个单变点检测问题。同时对每个估计变点构建了置信区间,为描述变点提供更多信息。最后通过大量数值模拟和交通实例分析证明方法的有效性。
关键词 :多变点,似然比,置信区间,最小描述长度准则

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近年来,变点检测一直被认为是计量经济学,生物学和统计学的一个重要问题。大量文献探索了时间序列模型中变点的检测。变点估计的第一篇文章是由Hinkley (1970)提出的,他研究i.i.d随机变量序列中变点的极大似然估计,并证明了估计变点依分布收敛于双侧随机游走的最大值,在正态假设下,表明其极限分布可以通过数值方法获得 [1] 。Hinkley (1970)使用类似的方法研究了服从二项分布的随机变量序列,并给出了极限分布的可计算形式 [2] 。但是,对于非正态或非二项分布的情况,其结果不能作为变点的统计推断。直到Yao (1987)表明当参数变化幅度d很小时,Hinkley (1970)的极限分布可以作为变点估计分布的一个良好近似 [3] 。在时间序列领域,Picard (1985)首先研究了自回归(AR)模型中变点的极大似然估计。她假设参数变化幅度是 , 取决于样本量n,当 时, ,结果得到与Yao (1987)相同的极限分布,这为本文后期对变点构建置信区间提供理论支持 [4] 。Davis (2006)提出利用最小描述长度 (MDL: Minimum description length)准则来检测非线性时间序列中的多变点 [5] 。Fryzlewicz (2014)提出wild二元分割(WBS: Wild Binary Segmentation)方法,省去复杂的优化过程,将非平稳时间序列随机分割为分段平稳序列,运用乘积性模型将时间序列自协方差结构中的变点检测问题转化为检测小波周期图中的变点问题 [6] 。Yau (2016)研究了非平稳时间序列中的多变点问题,通过似然比扫描方法将原始序列分解为一段一段的自回归过程,分别对各段AR过程进行建模,AR模型参数发生改变的点即为变点。随着这些方法的产生,非平稳时间序列中的多变点研究问题得到了快速发展 [7] 。
实际上,仅仅检测出变点位置并不能提供完整的信息,相比之下,置信区间可以提供更多信息来对变点进行描述。为了获得置信区间,则需要得到变点估计的渐近分布。Hinkley (1970)、Picard (1985)和Yao (1987)分别研究了估计变点的收敛情况及极限分布,指出变点估计依分布收敛于双侧随机游走的最大值,其极限分布参见Yao (1987)。
本文首先介绍了变点模型及其渐近理论。其次,结合似然比方法构造似然比扫描(LRS: Likelihood ratio scan)统计量进行变点检测,并给出相应的渐近性质及似然比扫描方法的详细执行步骤:1) 使用似然比扫描统计量获得初步变点估计(可能存在过估计问题,将一些不是异常点识别为变点);2) 采用MDL准则进行模型选择过程,进而得到一组一致变点估计;3) 为每个估计的变化点构建置信区间。最后,利用大量数值模拟和交通实例验证LRS方法的有效性、优良性和实用性。
2. 模型介绍
2.1. 基本假设
假设时间序列 是 可测的,并且严格平稳的,遍历的,可表示为
(1)
其中 是由 生成的 域, , 是 维的未知参数向量, 是独立同分布的。序列 的结构由可测量的函数g和参数 刻画,假设参数空间 是 的有界紧集,且g是关于 连续的。当真实参数 时,用 表示模型(1),同理 时,用 表示模型(1)。
首先考虑分段平稳过程中的单变点问题。设 是由两个独立过程组成的随机样本,记 为真实变点,满足 ,则单变点问题模型为
(2)
其中 是两段序列的未知参数,且 。
记条件似然函数 ,其中 是 给定过去观测值的条件密度函数。则单变点模型(2)的似然函数为
式中 , 分别是两段序列的条件对数似然函数。对于给定的 , ,同理 ,则变点 可由(3)式进行估计
(3)
变点前后两段的参数估计分别为 , 。 的一致性证明参见Ling (2016) [8] 。
2.2. 变点估计的渐近分布
对于单变点模型(2),定义随机游走
(4)
当 时 , 时 。参照Ling (2016)的定理2.2(b),对于固定的 , 有
(5)
注意到 的极限分布依赖于未知参数 , ,并且不能得出分布函数的解析式,因此,实践中难以直接使用(5)构造置信区间。Ling (2016)定理3.1推导出了当参数变化很小时 的近似分布。具体而言,如果 ,那么对于任意给定的
(6)
其中 , , , , , 是 上的标准布朗运动, (变点数目)。
进一步,记 的分布为 ,则当 时,有
因此
当M充分大时, 的概率很小,所以当d较小时,
成立。Yao (1987)证明了 的分布 具有密度函数:
(7)
其中 , 。故当M充分大,d较小时,可以用 来近似 的分布。利用 对变点估计进行置信区间构造,即 置信度的置信区间为
(8)
其中 , 是 的 分位数。
3. 基于似然比扫描 (LRS)方法的多变点估计
结合AR过程的计算优势和强稳健性,考虑将原始序列通过合理分割变为分段平稳AR过程,即将原始序列的多变点估计变为局部单变点估计。
3.1. 基本假设
假设观测值 可以划分为 个平稳过程。第j段序列观测值 ,其中 , 是第j个变点,即在 处第j段AR过程 发生突变,变为第 段AR过程 。令 , 。记 为变点的集合。定义 为第j个变点的相对位置,使得 , ,且满足当 时 。
3.2. 基于似然比扫描统计量的多变点检测步骤
本节,主要介绍了LRS方法检测多变点的三个步骤,其变点估计及渐近性质将在下节讨论。
第一步:使用似然比扫描统计量获得所有变点集合
分别定义扫描窗口及其相应的观测值为
,
其中 ,h称为窗口半径, 依赖于样本量n。定义扫描窗口 的似然比扫描统计量
, , 分别是相应观测序列 , , 的条件似然函数。具体地说,样本 的条件似然函数为
其中 是给定过去观测值的条件密度函数,且当 时 。
接下来,使用扫描统计量 对序列进行扫描,从而获得一组似然比扫描统计量值的序列 ,如果t是变点, 往往会较大。若 ,则每个扫描窗口内至多存在一个变点。因此 的局部最大值构成一组变点估计,记局部变点估计如下
当 时 。即如果 是扫描窗口 内的最大值,则m就是该扫描窗口的局部变点估计。记 为估计变点的数目,表示 中的元素个数。
第二步:通过模型选择得到变点一致估计
寻找m, 的最佳集合即为模型选择问题。从上一步获得的局部变点估计集合 通常会存在过估计问题,即将一些正常值也识别为变点,使得 内不仅包含所有真实变点集合,还包含一些非变点。为了更准确地检测到真实变点,进一步利用合适的信息准则从 中选取最佳的子集作为变点估计。最小描述长度(MDL)准则已经在很多实证研究中体现出显著的优势(如Davis et al. (2006, 2008)),本文选取MDL准则进行模型选择过程。给定一组变点估计 ,MDL准则定义为
式中 是第j段的似然函数, 是每段分割的长度, 是 的维数, 是整数值参数,分别确定第j段分割的模型参数 [5] [9] 。考虑本文将各段分为AR过程,整数值参数只有AR过程阶数 ;又 ,故 。所以针对AR过程,其MDL表达式为
给定局部变点估计 ,可以通过下式精确估计变点
因为 所包含的因素已经远远少于样本容量,所以在 上优化MDL使计算的复杂度大大降低,提高计算效率。本文采用Yao (1984)和Jackson (2005)提到的最优分割(OP)算法对MDL进行优化 [10] [11] 。
第三步:最终估计和置信区间构造
定义新扩展的局部窗口 和第j个变点估计 的相应观测值
,
这保证了每个真实变点在相应扩展局部窗口 的 内的概率接近于1。设 ,定义最终变点估计为
其中 , 类似定义。此时,可利用2.1中的结论来获得每个最终的变点估计 的置信区间。
在最初扫描步骤中, 的大小为2h,对给定h,每个时刻t的 的计算复杂度为 。在第二步中,使用Jackson (2005)最优分割算法优化MDL时,最小化MDL需要 的计算复杂度。
在第三步中,由于计算被限制在扩展的局部窗口上,所以计算复杂度为 。综上,由于 和 都是有限的,因此整个检测到最终变点估计过程的总计算复杂度为 。当h较小时,例如 ,则完整的三步LRS方法需要使用动态规划算法(最优分割算法)的计算复杂度为 ,明显低于 的数量级。如3.3节所示,窗口半径h作为调整参数,其值选取对定理3.1是至关重要的,其中d未知的。但如果h的阶数大于 ,例如 ,那 的取值不会影响到LRS方法的一致性。因此,随着样本量的增加,这个h的选择在理论上是合理的。经过大量模拟及实证研究发现通常 时,各种模型和样本有较好的结果,因此建议当 时使用 ,当 时使用 作为h的经验选择。
3.3. 渐近性质
本节主要讨论似然比扫描方法的渐近性质,给出相应定理以保证变点估计数目、位置、置信区间的一致性。
假设3.1. 对任意两个连续的分段 , ,当 ,条件似然函数的期望 在 处取得唯一的极大值,同理当 , 在 处取得唯一的极大值,且 。此外有
假设3.2. 在任意一个分段中, 是关于 的连续可测函数,且关于 几乎处处二阶可微。
假设3.3. 令 。对任意 ,存在 使得 成立。
假设3.4. 对任意 ,均存在可积函数 ,使得 , 。
下面定理3.1确保了所有变点都可以在 的h邻域中确定。
定理3.1. 记真实变点集合为 ,通过第一步扫描统计量得到的局部变点集合为 ,其中 。若假设3.1~3.4成立,且 ,则存在 ,当 时有
由于变点之间的最小距离为 ,所以真实变点数目 是有限的。但此时并不能保证 等于 。也就是说,变点的数量可能被高估,存在过估计问题。接下来定理3.2阐述了基于MDL准则模型选择方法产生的变点数量和位置的一致性。
定理3.2. 定理3.1成立条件下,当 时,有 。此外,若 ,则有
由于 ,定理3.2意味着 ,与经典收敛速率 相比,显然是不理想的。不过尽管如此,区间 覆盖真实变点 的概率接近依然1,这使扩展的局部窗口产生变点一致最终估计和置信区间变得可行。
定理3.3. 定理3.2成立条件下,若 ,同时假设3.4成立,则有
其中 是一个随机游走如下所示
特别地,此时 。
由于变点之间的最小距离远大于窗口半径h,即 ,扩展的局部窗口 之间的距离亦趋于无穷,所以在一些弱相依条件下,构造的CI是渐近独立的。此时可将2.2中获得单变点置信区间的方法直接应用至多变点模型(其实质也是局部单变点问题)。
4. 数值模拟
下面用数值模拟说明LRS方法的有效性。
4.1. 模型表达
模型A:没有变点的平稳AR(1)过程
模型A用来测试评估统计量在没有变点时的检测性能,即当序列无变点时,统计量是否能准确识别。AR(1)过程 ,设样本量 。
模型B:分段平稳AR(1)过程
模型C:分段平稳AR(2)过程
模型D:分段平稳分段平稳AR过程(3变点)
模型E:分段平稳ARMA(1,1)过程(2变点)
在模型对比中加入ARMA过程,试图拓展统计量在ARMA过程中的变点识别应用问题。


Figure 1. Location of true change-point and LRS estimation
图1. 各模型真实变点与LRS方法估计变点位置
Table 1. Location of true change-point and LRS estimation
表1. 各模型真实变点与LRS方法估计变点位置
结合表1和图1可看出,LRS对于非平稳时间序列中的变点检测问题是有效的,不论是单变点、多变点还是没有变点的情形,均可以较准确的进行检测。在ARMA过程中的变点位置检测会出现偏移,但变点个数均正确,尽管准确率有所下降,不难看出检测到的变点仍在构造的置信区间内。
4.2. 置信区间
本节主要检查变点置信区间的覆盖准确性。通过上述各个模型生成数据。应用LRS方法,在每个估计变点周围利用定理3.3和2.2节的结论构建90%置信区间。设置样本量 ,分别各进行100次模拟。结果如表2所示。
表2展示了具体结论,表明最终变点估计 对 做出了较好的估计,且置信区间覆盖概率较高,效果良好。
4.3. 模拟对比
定义利用渐近分布构造的置信区间覆盖率为CR
趋近于1,则认为估计效果比较好。
为对比检验LRS方法检测变点的准确率,依旧通过上述5个模型,同时利用LRS方法与经典WBS方法进行比较。各模型分别模拟100次,整理得到结果见表3。
Table 2. Confidence interval coverage of each model
表2. 各模型置信区间覆盖情况
Table 3. Simulation result of LRS and WBS
表3. LRS、WBS模拟结果
结果显示,当非平稳序列为分段平稳AR过程时LRS方法和WBS方法均能较好的检测出变点且位置估计效果都比较好,从变点个数检测和位置估计的准确率上来说,LRS方法准确率明显高于WBS方法,WBS方法存在较严重的变点数目高估问题,将一些本不是变点的点作为变点。通过上述典型模型的变点检测情况,明确了LRS方法的优良性,对各模型均能灵敏的对变点数目进行检测,给出了良好的变点位置估计,同时构建的置信区间覆盖率也较高,证明了LRS方法的实用性。
5. 交通流数据应用实例
以贵阳市宝山北路与东新区路交叉口南北方向车流量数据为例。选取2016年4月4日至2016年4月10日一周(星期一至星期日)车流量数据进行变点检测,验证LRS方法的实用性。数据为每天00:00~23:55每两分钟(共720个)过车数量。宝山北路与东新区路交叉口南北方向一周车流量时序图如图2所示。
考虑工作日、休息日车流量分布情况,分别选取星期四、五、六作为代表,同时利用LRS方法和WBS方法对车流量数据进行变点检测,分别得到各天的变点估计情况如图3~5所示。
Figure 2. Guiyang Baoshan North Road and East New Road intersection south to north one week traffic flow
图2. 贵阳市宝山北路与东新区路交叉口南向北一周车流量时序图

Figure 3. Intersection of Baoshan North Road and East New Roads Thursday, April 7, 2016 estimated traffic flow change point location
图3. 宝山北路与东新区路交叉口2016年4月7日(星期四)车流量变点位置估计

Figure 4. Intersection of Baoshan North Road and East New Roads Friday, April 8, 2016 estimated traffic flow change point location
图4. 宝山北路与东新区路交叉口2016年4月8日(星期五)车流量变点位置估计
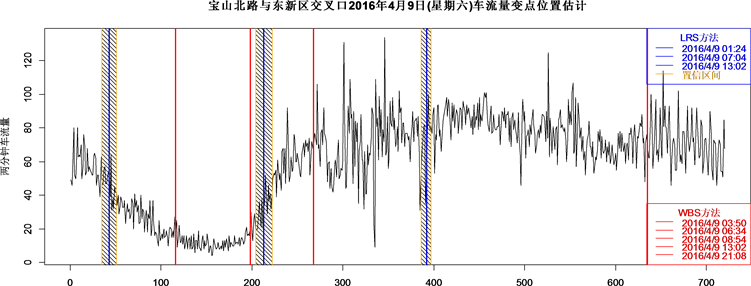
Figure 5. Intersection of Baoshan North Road and East New Roads Saturday, April 9, 2016 estimated traffic flow change point location
图5. 宝山北路与东新区路交叉口2016年4月9日(星期六)车流量变点位置估计
通过图3~5可直观清晰的对比两种方法对变点位置的估计情况,WBS方法检测出的变点数目明显多于LRS方法,过估计问题依然普遍存在。从工作日(星期四星期五)的变点位置不难虽然WBS方法估计变点多于LRS方法,但是LRS方法检测出的变点附近WBS方法也识别到了变点的存在,即对于变点的存在性检测两种方法都是足够灵敏的。区别较大的是休息日(星期六)的变点位置估计,LRS方法和WBS 方法检测出的点分别对应时间01:24、07:04、13:02和03:50、06:34、08:54、13:02、21:08。但从实际出发,该交叉路口处于贵阳市中心,很多大型商圈围绕,当星期五结束工作,晚上人们会集中前往娱乐消遣,与朋友聚会等,所以在01:24左右前还属于人群活动时间,成为新的出行“高峰”,01:24左右后人们才陆续休息,此时车流极具下降造成分布改变;休息日不存在早晚高峰问题,但考虑早晨人们开始起床活动或出游等造成07:04左右时交通流分布发生改变,车流量开始增多;非工作日贵阳车辆不实行尾号限行,所以全天车流都较多,在13:02后该路口车流量趋于平稳,分布不在发生改变。
表4展示了LRS方法和WBS方法对2016年4月4日(星期一)至2016年4月10日(星期日)每天车流量的变点识别情况,具体见表4。
Table 4. Contrast of change point of traffic flow data detection results
表4. 交通流数据变点检测结果对比
结果显示工作日(星期一至星期日) LRS方法普遍识别出3个变点,这3个点将车流量数据分为4个子序列,变点位置及对应的时间也相对较为固定,集中在早、中、晚上下班高峰期,与实际也比较符合。针对星期日车流数据LRS方法未识别到,原因可能为:1) 当天数据比较特殊,2) 星期日贵阳城区不限号,当日在所有时间段内车流分布都基本保持不变,尽管从凌晨到上午7点这段时间过车量较少,但并未导致整个车流分布发生改变。其次,WBS方法对变点的识别也是灵敏的,但是过估计问题也十分严重,常将一些奇异点也当作变点处理。通过数值模拟和实证分析都表明相较于目前使用较多的WBS方法,LRS方法不仅能有效识别到变点,而且能够更为准确的对变点位置进行估计,说明LRS方法对变点研究是实践可用的。
6. 结束语
文章考虑了分段平稳时间序列的变点检测问题,假设观测值服从参数不同的非线性时间序列模型(AR模型),且变点数量及位置均未知,通过构建LRS统计量对序列进行检测,实现序列变点的初步识别,进一步结合MDL准则进行模型选择,估计变点的数量、位置,最后对每个估计变点分别构造置信区间。同时利用WBS算法对序列变点数目及位置进行估计,并对两种算法进行模拟比较。数值模拟结果显示,两种方法均对变点有良好的识别效果,但LRS方法明显优于WBS方法,LRS方法的模型选择过程能更有效的剔除异常值,使得变点估计更为准确。最后,结合贵阳市中心道路车流量数据实例分析,表明方法对于交通流突变分析效果较好。
基金项目
贵州大学2017年研究生创新基金项目(研理工2017067);国家自然科学基金项目(11661018,11361015);全国统计科学研究项目(2014LZ46);贵州省自然科学基金项目(黔科合J字[2014]2058号)。
文章引用
吴 楠,胡 尧,王 丹. 分段平稳时间序列中的多变点检测
Multiple Change-Points Detection of Piecewise Stationary Time Series[J]. 理论数学, 2018, 08(02): 136-148. https://doi.org/10.12677/PM.2018.82018
参考文献
- 1. Hinkley, D.V. (1970) Inference about the Change-Point in a Sequence of Random Variables. Biometrika, 57, 1-17. https://doi.org/10.1093/biomet/57.1.1
- 2. Hinkley, D.V. and Hinkley, E.A. (1970) Inference about the Change-Point in a Se-quence of Binomial Variables. Biometrika, 57, 477-488. https://doi.org/10.1093/biomet/57.3.477
- 3. Yao, Y.C. (1987) Ap-proximating the Distribution of the Maximum Likelihood Estimate of the Change-Point in a Sequence of Independent Random Va-riables. Annals of Statistics, 15, 1321-1328. https://doi.org/10.1214/aos/1176350509
- 4. Picard, D. (1985) Testing and Esti-mating Change-Points in Time Series. Advances in Applied Probability, 17, 841-867. https://doi.org/10.2307/1427090
- 5. Davis, R.A. and Rodriguez-Yam, G.A. (2006) Structural Break Estimation for Nonstatio-nary Time Series Models. Journal of the American Statistical Association, 101, 223-239. https://doi.org/10.1198/016214505000000745
- 6. Fryzlewicz, P. (2014) Wild Binary Segmentation for Multiple Change-Point Detection. The Annals of Statistics, 42, 2243-2281. https://doi.org/10.1214/14-AOS1245
- 7. Yau, C.Y. and Zhao, Z. (2015) Inference for Multiple Change Points in Time Series via Likelihood Ratio Scan Statistics. Journal of the Royal Statistical Society, 2015, 78. http://doi.org/10.1111/rssb.12139
- 8. Ling, S. (2016) Estimation of Change-Points in Linear and Nonlinear Time Series Models. Econometric Theory, 32, 402-430. https://doi.org/10.1017/S0266466614000863
- 9. Davis, R.A., Lee, T.C.M. and Rodriguez-Yam, G.A. (2008) Break Detection for a Class of Nonlinear Time Series Models. Journal of Time Series Analysis, 29, 834-867. https://doi.org/10.1111/j.1467-9892.2008.00585.x
- 10. Yao, Y.C. (1984) Estimation of a Noisy Discrete-Time Step Function: Bayes and Empirical Bayes Approaches. Annals of Statistics, 12, 1434-1447. https://doi.org/10.1214/aos/1176346802
- 11. Jackson, B., Scargle, J.D., Barnes, D., et al. (2005) An Algorithm for Optimal Partitioning of Data on an Interval. IEEE Signal Processing Letters, 12, 105-108. https://doi.org/10.1109/LSP.2001.838216
NOTES
*通讯作者。
