Pure Mathematics
Vol.
09
No.
02
(
2019
), Article ID:
29192
,
5
pages
10.12677/PM.2019.92019
Some Criticism on the Basic Concept of Infinite Set Theory
Maotuo Guo
School of Mathematics and Systems Sciences, Beihang University, Beijing

Received: Feb. 14th, 2019; accepted: Mar. 4th, 2019; published: Mar. 11th, 2019

ABSTRACT
Cantor’s Set theory is the basis of modern mathematics, especially calculus theory, but there are many logical loopholes in its theory. It is necessary to point out clearly for criticism. Historically, Cantor used the diagonal method to prove the uncountable nature of real numbers, but this proof has the following problems: Cantor uses infinitesimal numbers to prove which is not tight, actually real numbers and infinite decimals are not equivalent; in the process of proof with infinite decimals, numbers will be missed; the premise of Cantor’s proof is that “the part can be one-to-one with the whole”. This assumption is not proved and therefore cannot explain its rationality. Finally, in this paper, Cantor’s “one-to-one correspondence with the whole” can be used to derive the opposite result from the traditional set theory, so as to explain its absurdity in more detail.
Keywords:Cantor, Infinite Set, Potential, One-to-One Correspondence
对无穷集合论基本概念的几点批判
郭猫驼
北京航空航天大学数学与系统科学学院,北京

收稿日期:2019年2月14日;录用日期:2019年3月4日;发布日期:2019年3月11日

摘 要
Cantor集合论是现代数学尤其是微积分理论的基础,但其理论存在诸多逻辑漏洞,有必要明确指出,供学界批判。历史上,Cantor使用对角线法证明来实数的不可数性质,但是这种证明存在如下问题:Cantor使用无限小数进行证明具有不严密性,实数和无限小数并非等价的关系;使用十进制小数进行证明,在证明过程中会漏掉 个数;Cantor的证明的前提假设是“局部可以和整体进行一一对应”,这个假设未经证明因而不能说明其合理性。最后,本文在Cantor的关于“局部可以和整体一一对应”的前提下推导出了与传统集合论相反的结果,从而更加详尽的说明其荒谬性。
关键词 :康托,无穷集合,势,一一对应

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. Cantor集合论的历史背景和意义
1.1. 无穷集合的早期研究
无穷集合论是德国数学家Cantor (G. Cantor 1845~1918)于19世纪70年代创立的。由于数学公理化的必然要求,它成为整个数学的理论基础之一。Cantor的工作主要围绕无穷集合论展开,这些成果为分析学提供一种比较集合大小的重要方法。但是,这些“最伟大的工作”从一开始就饱受争议 [1]。随着人们对无穷研究的深入,其深层次的矛盾逐渐暴露了出来。
Cantor集合论主要围绕无穷集合概念展开 [2]。从希腊时代开始,无穷概念能否作为完成了的整体存在这个问题一直被数学家们和哲学家们关注和讨论。两种对立的观点分别称为潜无穷观和实无穷观。亚里士多德最先提出并对它们加以区别 [3]。这种争论一直持续到中世纪,但是一直被数学工作者所忽视,直到十七世纪微积分的诞生,微积分的逻辑基础问题的严密性问题使得数学家有必要对“无穷”这一幽灵进行解释。
事实上,牛顿和莱布尼茨的理论都建立在无穷小分析的基础上,前者的理解和运用是混乱的,后者的思想也不能自圆其说。柯西为此付出极大努力,企图用极限概念来弥补这个缺陷,但是他并没有解释作为极限存在合法性保证的实数系为什么完备的。之后,魏尔斯特拉斯和Dedekind也做过严密性相关的工作,他们都发现必须研究无穷集合的性质,因为数与连续性的定义中一定要涉及。
1.2. Cantor集合论的诞生
1870年至1872年,Cantor用三篇论文证明了三角级数唯一性的几个问题,其中讨论了间断点是某种无穷集合的情形。这里Cantor定义了一些集合论的概念,这是从“唯一性问题”的探索走向点集论研究的开端,并为点集论奠定了理论基础。而另一方面,他就是通过对“唯一性问题”的研究而认识到无穷集合的重要性,并开始从事无穷集合一般理论的研究。
Cantor赞同“整体可以和局部一一对应”的观点,认为反对无穷的观点是错误的。对Cantor来说,能够与自己的一部分构成一一对应的集合就是无穷集合。为了研究正整数集合和实数集合有别于完备性的另一种差异,Cantor在1873年提出了导致集合论产生的关键问题:正整数集合 与实数集合 之间能否一一对应。同年,他成功地证明了实数的“集体”不可数,也就是它不能同正整数的“集体”一一对应。1874年,他又提出了“可数集”的概念,以一一对应为准则对无穷集合进行分类。他把凡是能够与正整数集合构成一一对应的集合都称之为可数集,这是最小的无穷集合。随后他得到了一些重要结果:1) 有理数集合是可数的;2) 一切代数数是可数的;3) 任何有限线段上的实数不可数;4) 超越数不可数;5) 一切无穷集并非都是可数的,无穷集同有穷集一样也有数量上的区别。在论证了相同的势与不同的势的集合都存在之后 [4],Cantor继续深入研究他的势的概念,并引进了基数与序数的概念,特别是创造了超限基数和超限序数。从1879年到1883年,Cantor写了6篇论文,发展了这个工作,其中还涉及集合论在分析上的一些应用。该文从内容到叙述方式都与现代的朴素集合论基本一致,标志着点集论体系的建立。其中《对超穷集合论基础的贡献》标志着集合论从点集论向抽象集合论的过渡。
1.3. Cantor集合论的意义
由于各种数学理论的基础概念都可以用“集合”及隶属关系定义出来,因此可以认为集合论是全部数学理论的基础。Cantor在集合论中通过一一对应关系将有穷集合和无穷集合区别开来,一个可数集尽管是无穷的,但当它和不可数集对比时,它的无穷性就显得无足轻重了。数学家们逐渐发现,在解决一些重要问题时,“不值一提”的可数集是有用的。但当认清Cantor集合论的本质时,这样广泛而重要的应用反而变成了一个可怕的事实。
2. 无穷集合论的新观点
2.1. 集合的基数与势
Cantor研究无穷集合论,引进了无穷点集的一些概念,如:基数,势,序数等,试图把不同的无穷离散点集和无穷连续点集按某种方式加以区分。
集合的基数是指衡量这个集合大小的值。对于有限值,如 的基数为3;空集的基数为0等等。因此两个集合的基数相等当且仅当它们之间存在一一对应。按照这一原则,要说明一个集合M的基数比另一个集合N的大,就必须证明下述两点。
1) M与N不对等(即不存在一一对应的关系)。
2) M的一个子集与N对等。
其中:1) 保证M与N的基数不相等;2) 保证M的基数不比N的小。需要指出的是一个有限集不可能与其任意真子集对等 [5]。
集合的基数最基本的为 和 , 指的是该集合可以与自然数集N建立一一对应的关系,集合的势 指的是(0, 1)区间内的实数的个数, 和 为不同的势的关键在于证明(0, 1)区间内的实数是否是不可数的。
假设可以把(0, 1)区间内的实数按照某个顺序排列好,因为实数可以用小数表示出来,所以(0,1)内的实数是这样的
(其中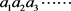 都是正整数)。假设排列好的数字是这样的:
都是正整数)。假设排列好的数字是这样的:
现在构造这样一个数 ,其中
因为已经按照某种顺序排列好了(0, 1)内的数,所以这样的b一定是可以构造出来的,并且显然b属于(0, 1),但是b又不在以上排列好的序列里,这就产生了矛盾。所以(0, 1)内的实数是不可数的,进而整个实数集也是不可数的。
2.2. 一维和二维空间点的对应
无穷集合论产生了很多背离直观的结论,比如一维实直线上的点与二维平面上的点一样多,考虑到实数的二维平面和复平面是等价的,故要证明一维实直线上的点与二维平面上的点一样多,只需证明实数和复数一样多。
本文可以把实数x的小数表达式的奇数位和偶数位分开,各构成一个实数 。由此构造复数 。按照此构造法,本文可以把实数和复数一一对应,即直线和平面的点一一对应。
3. 康托集合论证明的几点批判
3.1. 关于Cantor对角线法证明实数不可数的批判
Cantor基于角线法证明实数不可数存在前提性错误,因为实数与无限小数并非等同的关系,或者说实数不可以写成无限不循环的小数。这里,讨论的是纯数学问题而不是应用数学的问题。
有理数肯定不是无限不循环小数,无理数也只是它本身,也不是无限不循环的小数。无限小数是动态的,不确定的数。而无理数则是静态的确定的数,如果从序列的角度来看,无理数应该是无限不循环小数序列的极限,而不是这个序列本身或其中的某一个数,当然也不是这个动态过程。举个例子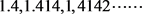 这个序列的极限是
。但是,
既不能算是那个序列,也不能等于序列中的某一个数。而Cantor却错误的将无理数等同于该无理数对应的无限不循环小数序列的动态过程。也就是说,Cantor把无限不循环小数序列的极限与无限不循环小数序列的动态延续混为一谈。
这个序列的极限是
。但是,
既不能算是那个序列,也不能等于序列中的某一个数。而Cantor却错误的将无理数等同于该无理数对应的无限不循环小数序列的动态过程。也就是说,Cantor把无限不循环小数序列的极限与无限不循环小数序列的动态延续混为一谈。
再者,除了上述的问题以外,就算错误的承认实数可以写成无限不循环的小数,仍会得到错误的结论。设[0, 1]区间的实数的无穷小数表式是二进制的,则其前n位就有2n种不同的排列方式,可以表示2n个由前n位不同的排列方式决定的不同的无穷小数表式下的实数,但在康托对角线法所依赖的原则下,显然只能表出其中的n个,有 个必被遗漏,当n趋向无穷时,此式始终成立,于是应有 个数被遗漏, 而由Cantor对角线法新产生的那个实数,仅为也必为其中之一 [6]。在实际中Cantor对角线法则采用的是十进制的方式,则可以得出必有 个数在排列中被遗漏。而产生此种结果的原因是对角线法中要求展开的小数的位数与排列的个数之间产生一一对应的关系,这种对应的关系也是Cantor对角线法的关键,但是由此也产生了排列的实数的遗漏的情况。退一步来说,这种一一对应的关系是一定成立的吗?Cantor在这里定义下了一个隐含的“公理”。没有这样的一个隐含的“公理”,对角线法的前提就有问题,自然对角线法本身就是错误的。
3.2. 部分真的可以和整体一一对应吗?
Dedekind曾说“如果系统S与其适当的部分相似,则它是无限系统;反之,则S为有限系统。”在这样的定义之下,无穷集合作为逻辑上相容的实体就存在了。这就是Cantor先生及其追随者希望接受的集合论“局部与整体可以一一对应”的前提。
实际上,假设A、B、C、D、E为无限集合,并且 ,再设 ,则E一定是作为A的真子集。A中的真子集C足以与E产生一一对应,这个可以有公理作为保证(两个相同的集合之间可以产生一一对应关系),故而,E中再无元素可与B和D两个集合产生对应。这样一个简单的证明,对有限集合和无限集合都是适用的。而Cantor只是看到A和E中的元素是无限的,就不区分两个集合的增长速度而举出一种对应的方式,这个是比较可笑的。他仅仅认为E中有无穷的多的元素,就认为E中的元素可以和A中的元素一一对应下去。但是却忽略了A集合中的自己C是和E集合有同步的无穷多的,由此在A的另外两个集合中是找不到对应项的。如果Cantor一定要认为集合A可以和集合E之间产生一一对应关系,或者说局部与整体可以一一对应方式,就应该给出这个方式的相应的证明。
也许有一些人会认为“通过具体的列举的方式就可以证明(比如自然数与偶数的对应方式,就可以通过具体列举的方式进行对应)。”但是这两个集合是无穷集合,谁能够列举的完全呢?并且可以看到就自然数 ,偶数 而言,他们在对应的时候n的取值应该是同步的,即使到了无穷大,n也应该是同步的。所以自然数集合应该是偶数集合的2倍。由此可见,忽视增长速度的列举方式是不正确的。
也会有人表明“这是有限集合的逻辑。”但是主张无限集合具有上述特征逻辑的人却没有给出令我们信服的证明。他们不也承认实数集合不能与全体的自然数集合一一对应吗?布尔巴基学派核心成员F.豪斯道夫说:“这一违反公理‘全体大于部分’的事实,既是‘无限矛盾之一’,对此我们必须习惯……” [7]。对此,我们只能感到无限的悲哀。
4. 结论
本文详细论述了Cantor集合的历史发展过程以及它的主要内容。然后针对Cantor集合论中关于实数对角线法的证明,以及其中Cantor关于无限集合的“局部可以和真题一一对应的原则”,进行了针对性的批判。本文认为对角线法则把数学写成无限不循环小数,而纯数学认为一个序列并不是数的本身,也就是动态的无限不循环小数并非实数本身。Cantor在用对角线法证明的过程中首先是暗含了一个公理似的前提“小数点后面的位数必须和实数的个数相同”,这个前提是不能证明的,而且在此前提下,Cantor的对角线法在罗列实数时也缺失了 个数。对于“局部与整体的一一对应”,本文认为Cantor的前提同样不可靠的,他不能给出确切证明。
进而,本文在“自身与自身的一一对应”的基础上,推导出和Cantor集合论完全相反的结论。在科学的发展道路上,我们要勇于思考,不应当盲目崇拜。以上的观点可能不一定完全正确,但是按照驳论的原则,只要我们有一点正确,那么Cantor集合论的基础就是有问题的。
致谢
在本文末尾,我要感谢北京高校青年微积分小组成员在写作构思和过程中给予的帮助和指导。
文章引用
郭猫驼. 对无穷集合论基本概念的几点批判
Some Criticism on the Basic Concept of Infinite Set Theory[J]. 理论数学, 2019, 09(02): 147-151. https://doi.org/10.12677/PM.2019.92019
参考文献
- 1. (美)莫里斯•克莱因. 古今数学思想[M]. 上海: 上海科学技术出版社, 2002: 167-168.
- 2. 沈汝彪. 集合论的孕育与诞生[J]. 数学通报, 2000(5): 38-40.
- 3. 杨文涛. 集合论的创立与发展[J]. 株洲师范高等专科学校学报, 2004(5): 53-55.
- 4. (美)莫里斯•克莱因. 古今数学思想[M]. 上海: 上海科学技术出版社, 2002: 162-163.
- 5. 钱建国. 集合的基数与一一对应原理[J]. 青海师范大学学报(自然科学版), 1998(4): 50-51.
- 6. 沈卫国. 论康托对角线法的局限性与数学、逻辑学中的一些基础性问题[J]. 天津职业院校联合学报, 2008(3): 114-123.
- 7. R.科朗, H.罗宾. 什么是数学[M]. 第二版. 上海: 复旦大学出版社, 2008: 95-97.