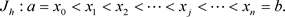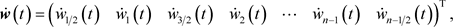ABSTRACT

In order to solve the problem of parameter identification for a class of parabolic differential equations with additional conditions, the quadratic finite volume element method is proposed for semi-discretization in space and the quadratic continuous finite element method for complete discretization in time. The numerical solution of unknown function and control parameter stability is derived, and the error analysis of the corresponding format is given. Finally, a numerical example is given to verify the stability and effectiveness of the proposed scheme.

Keywords:Parameter Identification Problem, Quadratic Finite Volume Element, Quadratic Continuous Finite Element, Totally Discrete Scheme, Stability

一类抛物微分方程参数识别问题的二次有限体积元方法

马娟，李玲，熊之光

湖南科技大学，数学与计算科学学院，湖南 湘潭

收稿日期：2019年11月16日；录用日期：2019年11月29日；发布日期：2019年12月6日

摘 要

针对一个具有附加条件的一类抛物微分方程的参数识别问题，首先提出了在空间上采用二次有限体积元法进行半离散，在时间方向上进行二次连续有限元全离散，导出了未知函数和控制参数稳定的数值解法，并给出了相应格式的误差分析，最后给出一个数值例子验证了所研究计算格式的稳定性和有效性。

关键词 :参数识别问题，二次有限体积元，二次连续有限元，全离散格式，稳定性

Copyright © 2019 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 前言

抛物微分方程参数识别问题是微分方程反问题中的一种，反问题是当微分方程中除了未知解以外，还有某个系数或初始条件或边界条件也是未知的。

本文将研究如下偏微分方程的参数识别问题

$\{\begin{array}{l}\frac{\partial u\left(x,t\right)}{\partial t}-\frac{{\partial }^{2}u\left(x,t\right)}{\partial x^2}=p\left(t\right)u\left(x,t\right),x\in \left(a,b\right),t>0,\\ u\left(a,t\right)=\text{0},u\left(b,t\right)=\text{0},t\ge 0,\\ u\left(x,0\right)=f\left(x\right),x\in \left[a,b\right],\\ u\left(x^{*},t\right)=E\left(t\right),a<x^{*}<b,t\ge 0.\end{array}$ (1)

其中 $f\left(x\right),E\left(t\right)$ 为充分光滑已知函数， $p\left(t\right),u\left(x,t\right)$ 为未知函数。该问题可以描述热源的扩散、粒子振动、控制理论等许多物理现象，文 [1] [2] 利用Adomain分解法研究了该方程的解，文 [3] 中用几种有限差分法求解该方程，讨论并比较了它们的准确性和稳定性，文 [4] 中使用了二次拟插值法解决抛物型方程的参数识别问题，文 [5] [6] 对抛物型参数识别问题给出有限体积元方法的求解格式，本文将用二次有限体积元法求解该问题。本文将作如下安排：第2节给出空间上的二次有限体积元的半离散格式。第3节给出时间上的二次连续有限元的全离散格式。第4节给出全离散格式的误差分析，讨论其稳定性和收敛性。第5节给出数值例子来说明该方法的有效性。

2. 有限体积元格式

首先对问题(1)作如下函数变换

$r\left(t\right)={\text{e}}^{-{\displaystyle {\int }_0^{t}p\left(s\right)\text{d}s}},w\left(x,t\right)=r\left(t\right)u\left(x,t\right),$ (2)

则问题(1)变换如下：

$\{\begin{array}{l}\frac{\partial w\left(x,t\right)}{\partial t}-\frac{{\partial }^{2}w\left(x,t\right)}{\partial x^2}=\text{0},x\in \left(a,b\right),t>0,\\ w\left(a,t\right)=\text{0},w\left(b,t\right)=\text{0},t\ge 0,\\ w\left(x,0\right)=f\left(x\right),x\in \left[a,b\right],\\ r\left(t\right)=w\left(x^{*},t\right)/E\left(t\right),a<x^{*}<b,t\ge 0.\end{array}$ (3)

该定解问题中方程不含参数函数，比原问题要简单，而且前三式直接为关于 $w\left(x,t\right)$ 和 $r\left(t\right)$ 的正问题，继而就可以求出参数 $p\left(t\right)$。

下面给出空间上二次有限体积元离散的计算格式，对空间区间 $I=\left[a,b\right]$ 作如下剖分：

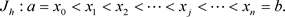
设单元 $I_j=\left[x_{j-1},x_j\right]$，步长 $h_j=x_j-x_{j-1}$,$h=\underset{1\le j\le n}{\max }{h}_j$，单元中点为 $x_{j-1/2}=\left(x_j+x_{j-1}\right)/2$，单元内四分点为 $x_{j\pm 1/4}=x_j\pm h_j/4$，并要求该剖分 $J_h$ 是拟一致剖分，即存在常数 $C>0$ 使得 $h\le C{h}_j$，此外再设

$\begin{array}{l}{I}_0^{\ast }=\left[x_0,x_{1/4}\right],I_{2i+1}^{\ast }=\left[x_{i+1/4},x_{i+3/4}\right]\left(i=0,1,2,\cdots ,n-1\right),\\ I_{2i}^{\ast }=\left[x_{i-1/4},x_{i+1/4}\right]\left(i=1,2,\cdots ,n-1\right),I_{2n}^{\ast }=\left[x_{n-1/4},x_n\right],\end{array}$

那么所有的 $I_i^{\ast }\left(i=0,1,\cdots ,2n\right)$ 构成 $J_h$ 的一个对偶剖分 $J_h^{*}$，每个 $I_i^{\ast }\left(i=0,1,\cdots ,2n\right)$ 为体积控制元。设试探函数空间为 $U_h=\left\{u|u\in C\left(I\right),u在每个单元I_j上为二次多项式\right\}$，对每个t， $w\left(x,t\right)$ 在单元 $I_j$ 上的基函数为：

$\{\begin{array}{l}{\phi }_{j-1}\left(x\right)=\frac{2}{h_j^2}\left(x_j-x\right)\left(x_{j-1/2}-x\right),\\ {\phi }_{j-1/2}\left(x\right)=\frac{4}{h_j^2}\left(x_j-x\right)\left(x-x_{j-1}\right),\\ {\phi }_j\left(x\right)=\frac{2}{h_j^2}\left(x-x_{j-1/2}\right)\left(x-x_{j-1}\right),\end{array}$

则定义插值算子 ${\Pi }_2:C\left(I\right)\to U_h$ 使得对任意的 $w\left(x,t\right)\in U_h$ 表示为

${\Pi }_2{w}_h={\displaystyle \underset{j=0}{\overset{n}{\sum }}{w}_j\left(x\right){\phi }_j}\left(x\right)+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{w}_{j-1/2}\left(x\right){\phi }_{j-1/2}}\left(x\right).$

再设函数空间 $V_h$ 为分片常数空间，对每个t， $w\left(x,t\right)$ 在基于节点 $x_j,x_{j+1/2}$ 上的对偶单元 $I_i^{*}$ 的基函数为：

$\begin{array}{l}{\psi }_j\left(x\right)=\{\begin{array}{l}1,x\in I_{2j}^{\ast },\\ 0,其他,\end{array}j=0,1,2,\cdots ,n,\\ {\psi }_{j+1/2}\left(x\right)=\{\begin{array}{l}1,x\in I_{2j+1}^{\ast },\\ 0,其他,\end{array}j=0,1,2,\cdots ,n-1,\end{array}$

则定义插值算子 ${\Pi }_2^{*}:C\left(I\right)\to V_h$，使得对任意的 $w\left(x,t\right)\in V_h$ 表示为

${\Pi }_2^{*}{w}_h={\displaystyle \underset{j=0}{\overset{j=n}{\sum }}{w}_j\left(t\right){\psi }_j\left(x\right)}+{\displaystyle \underset{j=1}{\overset{j=n}{\sum }}{w}_{j+1/2}\left(t\right){\psi }_{j+1/2}}\left(x\right),$

即对任意 $w_h\in U_h$,在单元 $I_j$ 可以表示为

$w_h=w_{j-1}\left(t\right){\phi }_{j-1}\left(x\right)+w_{j-1/2}\left(t\right){\phi }_{j-1/2}\left(x\right)+w_j\left(t\right){\phi }_j\left(x\right),$

其中 $w_j\left(t\right)=w_h\left(x_j,t\right),w_{j-1/2}\left(t\right)=w_h\left(x_{j-1/2},t\right)$，且 $w_0\left(t\right)=w_h\left(a,t\right),w_n\left(t\right)=w_h\left(b,t\right)$。

则(3)的二次有限体积元半离散为：固定变量t，寻求 $w_h\left(t\right)\in U_h$，使得，

$\{\begin{array}{l}{\displaystyle {\int }_{I_i^{*}}\frac{\partial w_h\left(x,t\right)}{\partial t}\text{d}x}-{\displaystyle {\int }_{I_i^{*}}\frac{{\partial }^2{w}_h\left(x,t\right)}{\partial x^2}\text{d}x}=\text{0},i=1,\cdots ,2n-1,\\ w_0\left(t\right)=w_n\left(t\right)=\text{0},\\ w_h\left(0\right)={\Pi }_{2}f\left(x\right)\in U_h,\end{array}$

即

$\{\begin{array}{l}{\displaystyle {\int }_{x_{i+1/4}}^{x_{i+3/4}}\frac{\partial w_h\left(x,t\right)}{\partial t}\text{d}x}-{\displaystyle {\int }_{x_{i+1/4}}^{x_{i+3/4}}\frac{{\partial }^2{w}_h\left(x,t\right)}{\partial x^2}\text{d}x}=\text{0},i=0,1,\cdots ,n-1,\\ {\displaystyle {\int }_{x_{i-1/4}}^{x_{i+1/4}}\frac{\partial w_h\left(x,t\right)}{\partial t}\text{d}x}-{\displaystyle {\int }_{x_{i-1/4}}^{x_{i+1/4}}\frac{{\partial }^2{w}_h\left(x,t\right)}{\partial x^2}\text{d}x}=\text{0},i=1,\cdots ,n-1,\\ w_0\left(t\right)=w_n\left(t\right)=\text{0},\\ w_h\left(0\right)={\Pi }_{2}f\left(x\right)\in U_h,\end{array}$

引入如下记号：

$w\left(t\right)={\left(\begin{array}{lllllll}{w}_{1/2}\left(t\right)\hfill & w_1\left(t\right)\hfill & w_{3/2}\left(t\right)\hfill & w_2\left(t\right)\hfill & \cdots \hfill & w_{n-1}\left(t\right)\hfill & w_{n-1/2}\left(t\right)\hfill \end{array}\right)}^{\text{T}},$

${\alpha }_0={\left(\begin{array}{lllllll}f\left(x_{1/2}\right)\hfill & f\left(x_1\right)\hfill & f\left(x_{3/2}\right)\hfill & f\left(x_2\right)\hfill & \cdots \hfill & f\left(x_{n-1}\right)\hfill & f\left(x_{n-1/2}\right)\hfill \end{array}\right)}^{\text{T}},$

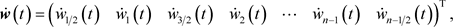
则可以得到二次体积元半离散的形式，用矩阵表示为如下满足初始条件的一阶线性常微分方程组

$\{\begin{array}{l}A\stackrel{\dot{}}{w}\left(t\right)=Bw\left(t\right),\\ w\left(0\right)={\alpha }_0.\end{array}$ (4)

其中

$A=\frac{h}{48}{\left[\begin{array}{ccccccccccc}22& 1& 0& 0& 0& 0& \cdots & 0& 0& 0& 0\\ 5& 16& 5& -1& 0& 0& \cdots & 0& 0& 0& 0\\ 0& 1& 22& 1& 0& 0& \cdots & 0& 0& 0& 0\\ 0& -1& 5& 16& 5& -1& \cdots & 0& 0& 0& 0\\ 0& 0& 0& 1& 22& 1& \cdots & 0& 0& 0& 0\\ 0& 0& 0& -1& 5& 16& \cdots & 0& 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& 0& 0& 0& \cdots & 1& 22& 1& 0\\ 0& 0& 0& 0& 0& 0& \cdots & -1& 5& 16& 5\\ 0& 0& 0& 0& 0& 0& \cdots & 0& 0& 1& 22\end{array}\right]}_{\left(2n-1\right)\times \left(2n-1\right)},$

$B=\frac{1}{h}{\left[\begin{array}{ccccccccccc}-4& 2& 0& 0& 0& 0& \cdots & 0& 0& 0& 0\\ 2& -4& 2& 0& 0& 0& \cdots & 0& 0& 0& 0\\ 0& 2& -4& 2& 0& 0& \cdots & 0& 0& 0& 0\\ 0& 0& 2& -4& 2& 0& \cdots & 0& 0& 0& 0\\ 0& 0& 0& 2& -4& 2& \cdots & 0& 0& 0& 0\\ 0& 0& 0& 0& 2& -4& \cdots & 0& 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& 0& 0& 0& \cdots & 2& -4& 2& 0\\ 0& 0& 0& 0& 0& 0& \cdots & 0& 2& -4& 2\\ 0& 0& 0& 0& 0& 0& \cdots & 0& 0& 2& -4\end{array}\right]}_{\left(2n-1\right)\times \left(2n-1\right)}.$

3. 二次连续有限元全离散格式

将时间部分有界区间 $J=\left[0,T\right]$ 作拟一致剖分： $0=t_0<t_1<\cdots <t_j<\cdots <t_{n_1}=T$，时间单元 $J_m=\left[t_{m-1},t_m\right]$ 的中点为 $t_{m-1/2}=\left(t_m+t_{m-1}\right)/2$，步长为 $l_m=t_m-t_{m-1}$,且记 $l=\underset{1\le m\le n_1}{\max }\left\{l_m/2\right\}$。对任意 $U={\left(u_1,u_2,\cdots ,u_{2n-1}\right)}^{\text{T}}$,$V={\left(v_1,v_2,\cdots ,v_{2n-1}\right)}^{\text{T}}$，为了以下研究方便，可以定义一个向量运算“ $\circ$ ”： $U\circ V={\left(u_1{v}_1,u_2{v}_2,u_3{v}_3,\cdots ,u_{2n-1}{v}_{2n-1}\right)}^{\text{T}}$，其它运算同普通的矩阵和向量运算。

因为矩阵A是严格对角占优的，所以A是可逆的，记 $A^{-1}B=G$，则(4)中 $A\stackrel{\dot{}}{w}\left(t\right)=Bw\left(t\right)$ 可化为：

$\stackrel{\dot{}}{w}\left(t\right)=Gw(t)$

将上式两边与 $Z\left(t\right)={\left(z_1,z_2,z_3,\cdots ,z_{2n-1}\right)}^{\text{T}}\in {\left(P_1\left(t\right)\right)}^{2n-1}$ 作“ $\circ$ ”运算，并在单元 $J_m$ 上积分，有

${\displaystyle {\int }_{J_m}\stackrel{\dot{}}{w}\left(t\right)}\circ Z\left(t\right)\text{d}t={\displaystyle {\int }_{J_m}Gw\left(t\right)\circ Z\left(t\right)\text{d}t}.$ (5)

定义 $w\left(t\right)$ 在t方向上的二次连续有限元 $D\left(t\right)$ 使：

${\displaystyle {\int }_{J_m}\stackrel{\dot{}}{D}\left(t\right)\circ Z\left(t\right)\text{d}t}={\displaystyle {\int }_{J_m}GD\left(t\right)\circ Z}\left(t\right)\text{d}t.$ (6)

设 $D\left(t\right)=B_0^m+\left(t-t_{m-1}\right)B_1^m+{\left(t-t_{m-1}\right)}^2{B}_2^m,t\in \left[t_{m-1},t_m\right]$，其中 $B_0^m,B_1^m,B_2^m\in R^N$ 为待定常数向量，当 $t=t_{m-1}$ 时， $B_0^m=D\left(t_{m-1}\right)=D^{m-1}$ 为已知。我们可以分别取 $Z\left(t\right)={\left(1,1,1,\cdots ,1\right)}_{2n-1}^{\text{T}}\in {\left(P_1\left(t\right)\right)}^{2n-1}$ 和 $Z\left(t\right)={\left(t-t_{m-1},t-t_{m-1},t-t_{m-1},\cdots ,t-t_{m-1}\right)}_{2n-1}^{\text{T}}\in {\left(P_1\left(t\right)\right)}^{2n-1}$，即可得到关于 $B_1^m$ 和 $B_2^m$ 的广义方程组：

$\{\begin{array}{l}{l}_m{B}_1^m+l_m^2{B}_2^m=G\left[l_m{D}^{m-1}+\frac{1}{2}{l}_m^2{B}_1^m+\frac{1}{3}{l}_m^3{B}_2^m\right],\\ \frac{1}{2}{l}_m^2{B}_1^m+\frac{2}{3}{l}_m^3{B}_2^m=G\left[\frac{1}{2}{l}_m^2{D}^{m-1}+\frac{1}{3}{l}_m^3{B}_1^m+\frac{1}{4}{l}_m^4{B}_2^m\right],\end{array}$

既得

$\{\begin{array}{l}{B}_1^m={\left[I_N-\frac{1}{2}{l}_{m}G+\frac{1}{12}{\left(l_{m}G\right)}^2\right]}^{-1}\left[I_N-\frac{1}{2}{l}_{m}G\right]G{D}^{m-1},\\ B_2^m=\frac{1}{2}{\left[I_N-\frac{1}{2}{l}_{m}G+\frac{1}{12}{\left(l_{m}G\right)}^2\right]}^{-1}{G}^2{D}^{m-1}.\end{array}$

其中 $I_N$ 是 $N=\left(2n-1\right)$ 阶单位矩阵。

将上式求得的 $B_1^m,B_2^m$ 代入 $D\left(t\right)=B_0+B_1\left(t-t_{m-1}\right)+B_2{\left(t-t_{m-1}\right)}^2$ 中，并取 $t=t_m$ 得到：

$D^m=D^{m-1}+l_m{B}_1^m+l_m^2{B}_2^m={\left[I_N-\frac{1}{2}{l}_{m}G+\frac{1}{12}{\left(l_{m}G\right)}^2\right]}^{-1}\left[I_N+\frac{1}{2}{l}_{m}G+\frac{1}{12}{\left(l_{m}G\right)}^2\right]D^{m-1}.$ (7)

由于 $D^0=w\left(0\right)={\alpha }_0$，所以用此递推的方法就可以求出每个时间层的全离散数值解 $D^m$。此方法就是二次连续有限元法的全离散格式，是一种显示单步格式。

最后可以得到数值解 $r^m,u_j^m,p^m$ 的计算格式，由(2)和(3)式可知：

$r\left(t\right)=\frac{w\left(x^{*},t\right)}{E\left(t\right)},u\left(x,t\right)=\frac{w\left(x,t\right)}{r\left(t\right)},p\left(t\right)=-\frac{r^{\prime }\left(t\right)}{r\left(t\right)}.$

我们已由式(7)得到 $w\left(x^{*},t\right)$ 的数值解 $w_k^m$，由此可得以下数值解 $r^m,u_j^m,p^m$ 的计算格式：

$r^m=\frac{w_k^m}{E\left(t_m\right)},u_j^m=\frac{w_j^m}{r^m},p^m=-\frac{r^{m+1}-r^{m-1}}{2r^m{l}_m},$ (8)

其中 $r^m,u_j^m,w_j^m,p^m$ 分别对应为 $r\left(t_m\right),u\left(x_j,t_m\right),w\left(x_j,t_m\right),p\left(t_m\right)$ 的数值解。

4. 误差分析

下面对空间上的二次有限体积元半离散解和全离散格式进行误差分析，根据文 [7] [8] 我们有如下引理：

引理4.1 设 $w\left(x,t\right)$ 为式(3)的精确解， $w_h\left(x,t\right)$ 是式(4)的二次有限体积元半离散解，则有如下模误差估计：

$\Vert w\left(x_j,t\right)-w_h\left(x_j,t\right)\Vert \le C{h}^3.$

引理4.2 $w_h\left(x_j,t\right)$ 是式(4)的二次有限体积元半离散解， $w_j^m$ 是式(6)的二次有限元全离散解，则有如下误差估计：

$\Vert w_h\left(x_j,t_k\right)-w_j^m\Vert \le C{l}^4.$

引理4.3 设 $w\left(x,t\right)$ 为式(3)的精确解， $w_j^m$ 是式(6)的二次有限元全离散解则有如下误差估计：

$\Vert w\left(x_j,t_k\right)-w_j^m\Vert \le C{h}^3+C{l}^4.$

定理4.1设 $u\left(x,t\right)$ 为式(1)的精确解， $u_j^m$ 是由式(8)得到的二次有限元全离散解， $p\left(t_m\right),p^m$ 分别为参数 $p\left(t\right)$ 的精确解与数值解， $r\left(t_m\right),r^m$ 分别为参数 $r\left(t\right)$ 的精确解与数值解，则有如下误差估计：

$\Vert r\left(t_m\right)-r^m\Vert \le C_1{h}^3+C_1{l}^4,$

$\Vert u\left(x_j,t_m\right)-u_j^m\Vert \le C_2{h}^3+C_2{l}^4,$

$\Vert p\left(t_m\right)-p^m\Vert \le c_1\frac{h^3}{l}+c_2{l}^2.$

证明 $r\left(t\right)$ 的误差估计：

$\begin{array}{c}\Vert r\left(t_m\right)-r^m\Vert =\Vert \frac{1}{E\left(t_m\right)}\left(w\left(x^{*},t_m\right)-w_k^j\right)\Vert \\ \le \Vert \frac{1}{E\left(t_m\right)}\Vert \left(\Vert w\left(x^{*},t_m\right)-w_h\left(x^{*},t_m\right)\Vert +\Vert w_h\left(x^{*},t_m\right)-w_k^j\Vert \right)\\ \le M\left(C{h}^3+C{l}^4\right)\le C_1{h}^3+C_1{l}^4.\end{array}$

$u\left(x,t\right)$ 的误差估计：由于 $\Vert r\left(t_m\right)-r^m\Vert \le C_1{h}^3+C_1{l}^4<r\left(t_m\right)/2$ 且

$r\left(t\right)={\text{e}}^{-{\displaystyle {\int }_0^{t}p\left(s\right)\text{d}s}}>0,$

则有

$\Vert r^m\Vert =\Vert r^m-r\left(t_m\right)+r\left(t_m\right)\Vert \ge \Vert r\left(t_m\right)\Vert -\Vert r\left(t_m\right)-r^m\Vert \ge \frac{1}{2}r\left(t_m\right).$

从而有

$\begin{array}{c}\Vert u\left(x_j,t_m\right)-u_j^m\Vert =\Vert \frac{w\left(x_j,t_m\right)}{r\left(t_m\right)}-\frac{w_k^m}{r^m}\Vert \\ =\Vert \frac{w\left(x_j,t_m\right)\left(r^m-r\left(t_m\right)\right)+r\left(t_m\right)\left(w\left(x_j,t_m\right)-w_k^m\right)}{r\left(t_m\right)r^m}\Vert \\ \le \Vert \frac{w\left(x_j,t_m\right)}{r\left(t_m\right)r^m}\Vert \left(C_1{h}^3+C_1{l}^4\right)+\Vert \frac{1}{r^m}\Vert \left(C{h}^3+C{l}^4\right)\\ \le \left(M\Vert \frac{2w\left(x_j,t_m\right)}{r^2\left(t_m\right)}\Vert +\Vert \frac{2}{r\left(t_m\right)}\Vert \right)\left(C{h}^3+C{l}^4\right)\\ \le C_2{h}^3+C_2{l}^4\end{array}$

$p\left(t\right)$ 的误差分析：由Taylor展开式得

$r^{\prime }\left(t_m\right)=\frac{r\left(t_{m+1}\right)-r\left(t_{m-1}\right)}{2l_m}+o\left(l_m^2\right)$

从而有：

$\begin{array}{c}\Vert p\left(t_m\right)-p^m\Vert =\Vert -\frac{r\left(t_{m+1}\right)-r\left(t_{m-1}\right)}{2r\left(t_m\right)l_m}-\frac{o\left(l_m^2\right)}{r\left(t_m\right)}+\frac{r^{m+1}-r^{m-1}}{2r^m{l}_m}\Vert \\ =\frac{1}{2l_m}\Vert \frac{-r\left(t_m\right)\left(r\left(t_{m+1}\right)-r^{m+1}\right)+\left(r\left(t_{m+1}\right)-r\left(t_{m-1}\right)\right)\left(r\left(t_m\right)-r^m\right)+r\left(t_m\right)\left(r\left(t_{m-1}\right)-r^{m-1}\right)}{r\left(t_m\right)r^m}\Vert +\frac{o\left(l_m^2\right)}{\Vert r\left(t_m\right)\Vert }\\ \le \frac{1}{l_m}\left(\Vert \frac{2}{r\left(t_m\right)}\Vert \left(C_1{h}^3+C_1{l}^4\right)+\Vert \frac{r\left(t_{m+1}\right)-r\left(t_{m-1}\right)}{r^2\left(t_m\right)}\Vert \left(C_1{h}^3+C_1{l}^4\right)\right)+\frac{o\left(l_m^2\right)}{\Vert r\left(t_m\right)\Vert }\\ \le c_1\frac{h^3}{l}+c_2{l}^2\end{array}$

5. 数值例子

本小节求解如下参数识别问题的数值例子，通过误差数据来说明计算格式的有效性。

$\{\begin{array}{l}\frac{\partial u\left(x,t\right)}{\partial t}-\frac{{\partial }^{2}u\left(x,t\right)}{\partial x^2}=p\left(t\right)u\left(x,t\right),x\in \left[0,1\right],t>0,\\ u\left(0,t\right)=\text{0},u\left(1,t\right)=\text{0},t\ge 0,\\ u\left(x,0\right)=\sin \left(\pi x\right),x\in \left[0,1\right],\\ u\left(0.25,t\right)=\frac{\sqrt{2}}{2}{\text{e}}^{-t^2},t\ge 0.\end{array}$

已知问题的精确解为： $u\left(x,t\right)={\text{e}}^{-t^2}\sin \left(\pi x\right),p\left(t\right)={\pi }^2-2t$。

先作代换消去 $p\left(t\right)$ 后，在空间上用二次有限体积元法，在时间上用二次连续有限元全离散进行数值计算，取均匀空间步长为h和均匀时间步长 $\Delta t$。表1给出了当 $t=1$ 时，网格比为 $\Delta t/h=1$ 的节点在 $N=100,200,400,800$ 的绝对误差值。表2给出了当 $t=1$ 时，网格比为 $\Delta t/h^2={10}^2$ 的节点在 $N=100,200,400,800$ 的绝对误差值。

表1. 网格比为 $\Delta t/h=1$ 时 $u\left(x,1\right),p\left(t\right)$ 的绝对误差

表2. 网格比为 $\Delta t/h={10}^2$ 时 $u\left(x,1\right),p\left(t\right)$ 的绝对误差

从表1，表2可以看出用本章研究的数值方法进行抛物方程参数识别是有效而可靠的。它的精度不仅与剖分密度有关，还与时间和空间的相对密度有关，也就是说，当剖分密度越大，时间和空间的相对密度越大，则利用该方法的精度越高。

基金项目

本文为国家自然科学基金项目(11571102)资助课题。

文章引用

马 娟,李 玲,熊之光. 一类抛物微分方程参数识别问题的二次有限体积元方法
The Quadratic Finite Volume Element Method for a Parameter Identification Problem of Parabolic Differential Equation[J]. 理论数学, 2019, 09(10): 1139-1147. https://doi.org/10.12677/PM.2019.910140

参考文献