Pure Mathematics
Vol.
10
No.
03
(
2020
), Article ID:
34508
,
5
pages
10.12677/PM.2020.103023
Solution on Differential-Difference Equation of Fermat-Type
Bingmao Deng
School of Financial Mathematics and Statics, Guangdong University of Finance, Guangzhou Guangdong

Received: Feb. 17th, 2020; accepted: Mar. 4th, 2020; published: Mar. 13th, 2020

ABSTRACT
In this paper, we mainly discussed entire solutions with finite order of the following Fermat type differential-difference equation and obtained some interesting results.
Keywords:Fermat-Type Equation, Entire Function, Differential-Difference Equation

一类费马型微分–差分方程解的问题
邓炳茂
广东金融学院金融数学与统计学院,广东 广州

收稿日期:2020年2月17日;录用日期:2020年3月4日;发布日期:2020年3月13日

摘 要
本文主要研究了以下费马型微分–差分方程的有穷级整函数解的情形, 并获得了一些有趣的结论。
关键词 :费马型方程,整函数,微分–差分方程

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言及主要结果
假设读者熟悉亚纯函数Nevanlinna值分布理论的基本内容及相关标准符号(见参考文献 [1] [2] [3])。
例如,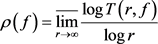 表示函数
的增长级,
表示所有
的小函数所构成的集合。
表示函数
的增长级,
表示所有
的小函数所构成的集合。
另外, 表示函数 的平移, , 分别表示其一阶差分及n阶差分。
在早期,对于费马型函数方程 解的讨论,已有许多经典结果 [4] [5] [6]。
在2004年,Yang and Li [6] 考虑了以下费马型微分方程解的情形,他们证明了
定理1. 设k是一个正整数, 是常数, 。则费马型方程 的超越亚纯解必具有以下的形式,
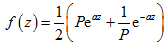 ,
,
其中 是非零常数,并且满足
,.
近年来,许多学者研究了差分方程、微分–差分方程解的存在性及增长性问题 [1] [7] - [12]。
2012年,Liu等人 [11] 研究了以下费马型差分–微分方程,并获得了以下结论。
. (1.1)
定理2. 方程(1.1)式的超越有穷级整函数解必定具有以下形式
,
其中, ,n是一个正整数,B是一个常数。
还有许多相关的结果,请参见文献 [13] [14] [15]。
本文的主要目的是研究方程(1.1)中的平移为高阶差分的解的形式问题,即研究
. (1.2)
本人主要证明了以下结论。
定理3. 设 是微分–差分方程(1.2)的有穷级整函数解,则 必定具有以下形式之一:
,或者
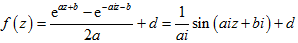 ,其中
是常数,并且满足
,
,其中
是常数,并且满足
,
,.
由定理3,可得以下推论。
推论1. 当(1.2)式中的 时,(1.2)式的解必具有以下形式:
,或者
,其中 是常数, 。
2. 一些引理
引理1 ( [3])设
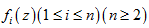 是亚纯函数,
是整函数,并且满足:
是亚纯函数,
是整函数,并且满足:
;
对任意的 , 时,均有
,,,
其中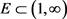 是对数测度有穷的集合。
是对数测度有穷的集合。
则 。
引理2 ( [3]) (Hadamard 分解定理)设 是有穷级整函数, 是其零点,并且0是其k重零点,则
,
其中 是由 除零之外的所有零点构成的典型乘积, 是一个满足 的多项式。
3. 定理3的证明
设 是方程(1.2)的有穷级整函数解,将(1.3)改写成下式
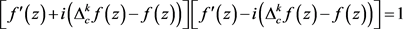 。 (3.1)
。 (3.1)
从(3.1)式可知, 与 均没有零点,由引理3,Hadamard分解定理可得:
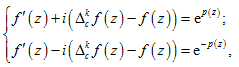 (3.2)
(3.2)
其中 是一个多项式。
解(3.2)式,可得
, (3.3)
. (3.4)
以下分两种情形讨论。
情形1. 是超越整函数。则由(3.3)式知, 是非常数多项式。令 ,则 。
对(3.4)式两边同时求一阶导,可得
. (3.5)
另一方面,由(3.3)式,可得
. (3.6)
结合(3.5)与(3.6)式,经简单计算可得
. (3.7)
合并同类项,即得
. (3.8)
若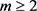 ,则对任意的
,均有
,则对任意的
,均有
, 且 .
由(3.8)式,结合引理2,可得 ,矛盾。
因此,
。因此,可设
,其中
。则
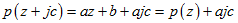 ,,与
。
,,与
。
(3.8)式两边同时乘以 ,并化简,可得
.
即
. (3.9)
由(3.9)式可得
. (3.10)
注意到 ,。由(3.10),可得
否则,由(3.10)式,有
,
即得 是一个常数,这与 矛盾。
从而
(3.11)
解(3.11)式,易得
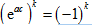 ,且
,。因此,
具有以下形式
,且
,。因此,
具有以下形式
.
情形2.
是多项式。则由(3.3)式可得
是一个常数,因此,
恒为常函数,从而
。如果
k ≥2,则显然
,代入(1.2)式,可得
,解得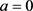 ,
。如果
,则
,代入(1.2)式,可得
,
。如果
,则
,代入(1.2)式,可得
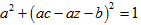 ,同样解得
,同样解得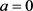 ,
。因此,
。
,
。因此,
。
定理3证明完毕。
基金项目
国家自然科学基金青年资助项目(11901119)。
文章引用
邓炳茂. 一类费马型微分–差分方程解的问题
Solution on Differential-Difference Equation of Fermat-Type[J]. 理论数学, 2020, 10(03): 162-166. https://doi.org/10.12677/PM.2020.103023
参考文献
- 1. Hayman, W.K. (1964) Meromorphic Functions. Clarendon Press, Oxford.
- 2. Yang, L. (1993) Value Distribution Theory. Springer-Verlag, Berlin.
- 3. Yi, H.X. and Yang, C.C. (2003) Uniqueness Theory of Meromorphic Functions. Science Press, Beijing.
- 4. Gross, F. (1966) On the Equation fn + gn = 1. Bulletin of the American Mathematical Society, 72, 86-88. https://doi.org/10.1090/S0002-9904-1966-11429-5
- 5. Gross, F. (1966) On the Equation fn + gn = hn. The American Mathematical Monthly, 73, 1093-1096. https://doi.org/10.2307/2314644
- 6. Yang, C.C. and Li, P. (2004) On the Transcendental Solutions of a Certain Type of Nonlinear Differential Equations. Archiv der Mathematik, 82, 442-448. https://doi.org/10.1007/s00013-003-4796-8
- 7. Chen, M.F., Gao, Z.S. and Du, Y.F. (2017) Existence of Entire Solutions of Some Non-Linear Differential-Difference Equations. Journal of Inequalities and Applications, 90, 17 p. https://doi.org/10.1186/s13660-017-1368-1
- 8. Chiang, Y.M. and Feng, S.J. (2008) On the Nevanlinna Characteristic of f(z+η) and Difference Equations in the Complex Plane. The Ramanujan Journal, 16, 105-129. https://doi.org/10.1007/s11139-007-9101-1
- 9. Laine, I., Rieppo, J. and Silvennoinen, H. (2005) Remarks on Complex Difference Equations. Computational Methods and Function Theory, 5, 77-88. https://doi.org/10.1007/BF03321087
- 10. Halburd, R.G. and Korhonen, R.J. (2006) Difference Analogue of the Lemma on the Logarithmic Derivative with Applications to Difference Equations. Journal of Mathematical Analysis and Applications, 314, 477-487. https://doi.org/10.1016/j.jmaa.2005.04.010
- 11. Liu, K., Cao, T.B. and Cao, H.Z. (2012) Entire Solutions of Fermat Type Differential-Difference Equations. Archiv der Mathematik, 99, 147-155. https://doi.org/10.1007/s00013-012-0408-9
- 12. Liu, K. (2015) Fermat Type Differential and Difference Equations. Electronic Journal of Differential Equations, 159, 1-10. https://doi.org/10.1186/s13662-015-0534-3
- 13. Gao, L.Y. (2017) On Entire Solutions of Two Types of Systems of Complex Differential-Difference Equation. Acta Mathematica Scientia, 37B, 187-194. https://doi.org/10.1016/S0252-9602(16)30124-2
- 14. 高凌云. 关于一类复微分-差分方程组的解[J]. 数学年刊, 2017, 38A(1): 23-30.
- 15. Gao, L.Y. (2016) Entire Solutions of Two Types of Systems of Complex Differential-Difference Equations. Acta Mathematica Scientia, 59, 677-684.