ABSTRACT

This paper mainly discusses how to numerically solve tridiagonal Toeplitz linear systems $Ax=b$ efficiently. Since the coefficient matrix A has a special structure, we can design a direct algorithm to quickly solve $Ax=b$. We will apply the above algorithm to the calculation of practical examples and find that the calculation precision of some examples is not as high as that of computer's machine accuracy. In order to improve the precision of algorithm, this paper further carries out iterative refinement to quickly solve the tridiagonal Toeplitz linear equations of $Ax=b$. Numerical experiments show that the computational accuracy of our algorithm can reach computer's machine accuracy by iterative refinement [1].

Keywords:Toeplitz Matrices, Iterative Refinement, Fast Algorithm

迭代精化下求解三对角Toeplitz线性方程组的快速算法

李姗¹，刘仲云¹，张育林²

¹长沙理工大学数学与统计学院，湖南 长沙

²Minho大学数学中心，布拉加，葡萄牙

收稿日期：2020年4月16日；录用日期：2020年5月5日；发布日期：2020年5月12日

摘 要

本文主要讨论如何对三对角Toeplitz线性方程组 $Ax=b$ 进行高精度数值求解。由于系数矩阵A这种比较特殊的结构，使得我们可以设计出快速求解 $Ax=b$ 的直接算法。我们将该算法应用到实际例子的计算过程中，发现大部分例子计算效果显著，但部分例子的计算精度还不能达到计算机机器精度。针对这类达不到计算机机器精度的例子，本文将在快速求解三对角Toeplitz线性方程组 $Ax=b$ 的直接算法基础上，进一步进行迭代精化，从而提高这类例子的计算精度。数值实验表明通过迭代精化，我们算法计算精度可以达到计算机机器精度 [1]。

关键词 :Toeplitz矩阵，迭代精化，快速算法

Copyright © 2020 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

本文考虑迭代精化下求解三对角Toeplitz线性方程组

$Ax=b,$ (1.1)

$A=\left[\begin{array}{cccc}\alpha & \gamma & & \\ \beta & \ddots & \ddots & \\ & \ddots & \ddots & \gamma \\ & & \beta & \alpha \end{array}\right]$

其中 $A=\text{Tritoep}\left(\beta \mathrm{,}\alpha \mathrm{,}\gamma \right)$ 为三对角Toeplitz矩阵。

关于三对角Toeplitz线性方程组的求解方法主要分为两类：一类是直接法如高斯消元法、循环约简法和特殊LU分解法 [2] [3] [4] 等等。另一类就是迭代法如古典迭代法(Smith迭代法，ADI迭代法 [5] [6] [7] [8] 等)和投影迭代法(Krylov子空间法等)。在不考虑舍入误差的情况下，对于小型稀疏求解线性方程组的问题，我们通常使用直接法求解。因为直接法可以通过改善置换策略，引入尽量少的填充，充分利用硬件的性能设计算法。但当遇到大型稀疏求解线性方程组的问题时，直接解法计算量太大且数值不稳定，而迭代解法数值稳定且易于并行计算，所以这时我们通常使用迭代法求解。

Toeplitz矩阵是一类特殊结构的矩阵，它在数学、科学计算和工程中有着广泛的应用，如信号处理中的图像恢复存储问题、代数微分方程、时间序列和控制理论等。本文主要讨论如何对三对角Toeplitz线性方程组 $Ax=b$ 进行高精度数值求解。由于系数矩阵A这种比较特殊的结构，我们在前面一篇论文中已经设计出快速求解 $Ax=b$ 的直接算法。其系数矩阵主要是上次对角占优、下次对角占优、若对角占优。具体情况如下：

我们首先从系数矩阵为次对角占优情况开始考虑。

$C=\left[\begin{array}{ccccc}0& 1& & & \\ & 0& 1& & \\ & & \ddots & \ddots & \\ & & & 0& 1\\ 1& & & & 0\end{array}\right]$

我们容易得到 $\hat{A}=CA$ 并且具有如下 $2\times 2$ 的块结构

$\begin{array}{l}\hat{A}=\left[\begin{array}{ccccc}\beta & \alpha & \gamma & & \\ & \beta & \alpha & \ddots & \\ & & \ddots & \ddots & \gamma \\ & & & \beta & \alpha \\ \alpha & \gamma & & & 0\end{array}\right]\equiv \left[\begin{array}{cc}{A}_{11}& p\\ w^{\text{T}}& 0\end{array}\right]\mathrm{.}\hfill \end{array}$ (1.2)

我们对 $\hat{A}$ 作如下的 $2\times 2$ 的块LU分解

$\hat{A}=\left[\begin{array}{cc}I& \\ w^{\text{T}}{A}_{11}^{-1}& 1\end{array}\right]\left[\begin{array}{cc}{A}_{11}& p\\ & -w^{\text{T}}{A}_{11}^{-1}p\end{array}\right]\mathrm{.}$ (1.3)

$-w^{\text{T}}{A}_{11}^{-1}p$ 是叫做 $\hat{A}$ 的Schur补。

同样地，要求问题(1.1)的解也就变成了求如下线性方程组的解

$\hat{A}x=\hat{b}$ (1.4)

其中 $\hat{b}=Cb={\left(b_2\mathrm{,}{b}_3\mathrm{,}\cdots \mathrm{,}{b}_n\mathrm{,}{b}_1\right)}^{\text{T}}$。对x和 $\hat{b}$ 做如下格式的划分

$x=\left[\begin{array}{c}{x}_1\\ x_n\end{array}\right],\hat{b}=\left[\begin{array}{c}{b}_2\\ b_1\end{array}\right]\mathrm{.}$

用块LU分解法分解(1.3)，我们就可以通过求下面方程的解来获得方程(1.1)的解

$(\begin{array}{l}{A}_{11}{x}_1+x_{n}p=b_2\mathrm{,}\\ w^{\text{T}}{x}_1=b_1\mathrm{.}\end{array}$ (1.5)

$(\begin{array}{l}{x}_n=\left(w^{\text{T}}v-b_1\right)/w^{\text{T}}u\mathrm{,}\\ x_1=v-x_{n}u\mathrm{.}\end{array}$ (1.6)

为了获得 $x={\left[x_1^{\text{T}}{x}_n\right]}^{\text{T}}$ 的解，我们首先求解如下方程中的 $u$ 和 $v$

$(\begin{array}{l}{A}_{11}u=p\mathrm{,}\\ A_{11}v=b_2\mathrm{.}\end{array}$ (1.7)

通过如下算法，我们得到式(1.7)中方程组的解 $u$ 和 $v$，具体算法如下：

我们注意到，为了得到(1.6)的解 $x_1$ 和 $x_n$，我们需要解(1.7)中的两个线性方程组，其中 $A_{11}$ 是一个上三对角矩阵。显然，向量 $u$ 和 $v$ 可以通过向后代入法求解。此外，由于 $A_{11}$ 是对角占优的，计算出的向量 $u$ 和 $v$ 都是稳定可靠的。

基于以上分析，我们现在可以重新设计求解(1.1)的算法如下

算法2的稳定性取决于第三步的求解 $x_n=\left(w^{\text{T}}v-b_1\right)/w^{\text{T}}u$。如果 $w^{\text{T}}u$ 不是足够小，那么 $x_n$ 的就是相当精确的。因此，我们可以得出结论，我们求解这类线性方程组的算法在数值上是稳定的，计算出的解是可靠的，如果A是下次对角占优的并且 $w^{\text{T}}u$ 不是足够小。

对于计算复杂度，我们的算法需要大约12n (flops)的浮点运算，选主元的LU分解法需要13n (flops)浮点运算，我们的方法与选主元的LU分解法相比需要更少的浮点运算量。对于内存存储空间，我们的算法只需要存储2个大小为n向量，少于选主元的LU分解法需要存储5个大小为n向量。特别是，我们的算法需要较少的数据传输。在数据传输过程中它只需要读取1个向量即右边的向量并写入一个向量(即方程的解)。但是选主元的LU分解法需要读取个向量。正如我们所知，现代计算机有多层的内存结构，有不同的存储级别，如较小的高速缓存和较大的低速磁盘存储。在计算过程中，数据在不同级别的高速缓存中传输。因此，较少数据传输的算法可能会显示出更好的计算性能。这使得该算法比选主元的LU分解方法更有效。

现在，我们考虑上次对角占优的情况。设J为交换对角矩阵，在交叉对角上为1 (从左下到右上)，其他地方为0，即

$J=\left[\begin{array}{ccccc}0& 0& \cdots & 0& 1\\ 0& 0& \cdots & 1& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 1& \cdots & 0& 0\\ 1& 0& \cdots & 0& 0\end{array}\right]\mathrm{,}$ (1.8)

因为A是上次对角占优的， $\tilde{A}=JAJ=\text{Tritoep}\left(\gamma \mathrm{,}\alpha \mathrm{,}\beta \right)$ 是下次对角占优的。因此，我们可以将原来的线性线性方程组(1.1)转化为以下新的线性方程组

$\tilde{A}\tilde{x}=\tilde{b}$ (1.9)

$\tilde{x}=Jx$，$\tilde{b}=Jb$。因此，结合算法2得到下面的算法3用于求解方程(1.1)。

由于J是一个置换矩阵，因此算法3的稳定性、计算复杂度和内存存储都与算法2相同。

最后，我们讨论了不可约对角占优的情形。已知，在这种情况下，A是一个H矩阵，使用LU分解法不需要选主元。显然，这种情况下LU分解法不会导致任何非零元素的填充，但需要更多的内存存储空间。为了避免这个问题，我们采用以下方法：

如果 $\beta >\gamma$，那么我们选择算法2解方程(1.1)，如果 $\beta <\gamma$，然后调用算法3解解方程(1.1)。我们把以上情况总结，得到综合算法如下：

算法4的计算复杂度和内存存储与算法2或3基本相同。

与选主元LU分解法相比，我们提出的三对角Toeplitz线性方程组快速直接算法(算法4)具有以下优点：不仅需要更少的计算时间和存储空间以及数据传输，而且具有更高的计算精度。我们将该算法应用到实际例子的计算过程中，发现大部分例子计算效果显著，但部分例子的计算精度还不能达到计算机机器精度。为解决这类问题，我们将在快速求解三对角Toeplitz线性方程组 $Ax=b$ 的直接算法基础上进行迭代精化(详情见算法5)，从而减小我们的计算误差，提高解的精度。

2. 迭代精化算法及收敛性分析

求解(1.1)的精化迭代法的迭代格式 [12] 为：

$x^{\left(k+1\right)}=x^{\left(k\right)}+d^{\left(k\right)}$ (2.1)

$A{d}^{\left(k\right)}=r^{\left(k\right)},r^{\left(k\right)}=b-A{x}^{\left(k\right)}$ (2.2)

其中 $x^{\left(0\right)}$ 为初始迭代向量， $k=\mathrm{0,1,}\cdots$。当 $d^{\left(k\right)}$ 为(2.2)的精确解时，迭代格式(2.1)~(2.2)退化为单步迭代精化。不难看出，该迭代格式可以提高解 $x^{\left(k\right)}$ 的精度。另外，如果我们用高精度方法求解(2.2)，那么我们把迭代格式(2.1)~(2.2)称为迭代精化。

引理2.1 [12] 假设不考虑舍入误差，精确计算残差 $r^{\left(k\right)}$，$d^{\left(k\right)}$ 为(2.2)的精确解，则 $x^{\left(k+1\right)}$ 为(1.1)的精确解 [9]。

证明：由(2.2)式知 $A{d}^{\left(k\right)}=r^{\left(k\right)}$，$r^{\left(k\right)}=b-A{x}^{\left(k\right)}$，从而 $A{x}^{\left(k+1\right)}=A{x}^{\left(k\right)}+A{d}^{\left(k\right)}=b$。这意味着 $x^{\left(k+1\right)}$ 是(1.1)的精确解，证毕。

结合引理2.1与算法4，我们得到迭代精化 [10] 的具体算法如下：

定理2.1 [12] 假设r是双精度并且 $\kappa \left(A\right)\cdot \epsilon <c\equiv \frac{1}{3n^{3}g+1}<1$，n表示矩阵A的阶数，g表示主元增长

因子， $\kappa \left(A\right)=\Vert A\Vert \cdot \Vert A^{-1}\Vert$。那么迭代精化收敛于：

$\frac{\Vert x^i-A^{-1}b\Vert }{\Vert A^{-1}b\Vert }=o\left(\epsilon \right)\mathrm{.}$ (2.3)

定理2.2 [12] 令 $x^{\mathrm{<mo>\; *\; </mo>}}$ 为线性方程组(1.1)的精确解。对第k步迭代，用算法5求解(2.2)的初始迭代向量均为 $d^{\left(0\right)}=x^{\left(0\right)}$ (其中 $x^{\left(0\right)}$ 为用算法4求得的线性方程组(1.1)的解)，相应的迭代序列为 $d^{\left(k\right)}$，且 $d^{\left(k\right)}$ 满足终止检验公式

$\eta =\frac{\Vert r^{\left(k\right)}-A{d}^{\left(k\right)}\Vert }{\Vert r^{\left(k\right)}\Vert }<\epsilon$ (2.4)

则迭代序列 $x^{\left(k\right)}$ 满足

$\Vert x^{\left(k+1\right)}-x^{\mathrm{<mo>\; *\; </mo>}}\Vert \le \kappa \left(A\right)\epsilon \Vert x^{\left(k\right)}-x^{\mathrm{<mo>\; *\; </mo>}}\Vert$ (2.5)

特别地，当 $\kappa \left(A\right)\epsilon <1$，迭代序列 $x^{\left(k\right)}$ 收敛到 $x^{(\ast )}$ [11]。

证明：由(2.1)、(2.2)及(2.4)式知

(2.6)

从而

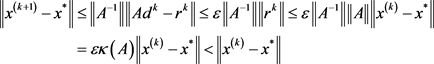(2.7)

当时，迭代序列收敛，证毕。

针对算法5，只要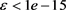，则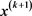满足终止检验公式(2.4)，那么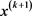就是满足计算机机器精度的解 [12]。

3. 数值实验

下面我们用一些例子证明我们算法的有效性。本文所有数值实验的电脑运行环境为：Intel(R) Core(TM) i3-2310M CPU @2.10 by Matlab 7.4.0.287 (R2014a)。分别用快速直接算法和加迭代精化的快速直接法分别对三对角Toeplitz线性方程组进行求解。选取典型代表例子如下：

例1：；

例2：。

在例1、例2中的矩阵A是由一维对流扩散方程离散差分得到的方程的系数矩阵。在所有例子中二阶差分都采用中心差分格式。但在例1和例2中一阶差分分别使用中心差分格式和向后差分格式。在数值实验中，我们计算了许多不同n和参数c的例子。我们可以得到共同的结论。接下来我们展示一些有代表性的例子结果。在实验中，n表示矩阵A的阶数，Iter表示迭代次数，CPU表示计算时间，右端向量

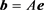，R表示计算相对残差，即()，Fast algorithm表示快速算法，Iter algorithm表示对快

速算法进行迭代精化。

数值结果表1是例1取和的两个例子，数值结果表2是例2取和的两个例子。我们发现当我们用直接算法1计算三对角Toeplitz线性方程组时，存在计算精度无法达到机器精度的情况。但是通过我们进一步迭代精化，当迭代一定次数(本例Iter = 10)时，我们的计算精度就可以达到计算机机器精度。

表1.

表2.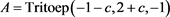

数值实验表明，当采用直接算法求解三对角Toeplitz线性方程组的时候，存在计算精度达不到计算机机器精度的情况。但是通过我们的迭代精化算法，可以使三对角Toeplitz线性方程组的解都能够达到计算机机器精度。

基金项目

2019年硕士研究生校级科研创新项目(CX2019SS34)。

文章引用

李 姗,刘仲云,张育林. 迭代精化下求解三对角Toeplitz线性方程组的快速算法
A Fast Algorithm for Solving Tridiagonal Toeplitz Linear Systems with Iterative Refinement[J]. 理论数学, 2020, 10(05): 425-432. https://doi.org/10.12677/PM.2020.105052

参考文献