短正合列的性质 The Nature of Short Exact Sequence

doi:10.12677/PM.2020.108085

Pure Mathematics
Vol. 10 No. 08 ( 2020 ), Article ID: 37035 , 7 pages
10.12677/PM.2020.108085

The Nature of Short Exact Sequence

Hongtao Fan

●How to Cite this Article

College of Mathematics and Information Science, Nanchang Hangkong Univerisity, Nanchang Jiangxi

Received: Jul. 21^st, 2020; accepted: Aug. 7^th, 2020; published: Aug. 14^th, 2020

ABSTRACT

In this paper, the short exact sequence composed of chain complex and chain mapping is studied. The edge homomorphism of homology sequence is defined and the proof of good definition is given. By using the short exact sequence composed of chain complex and chain map and the defined edge homomorphism, the naturalness of the positive congruent sequence and the homology sequence is derived and proved.

Keywords:Short Exact Sequence, Chain Complex, Homology Sequence

短正合列的性质

范宏涛

南昌航空大学，数学与信息科学学院，江西南昌

收稿日期：2020年7月21日；录用日期：2020年8月7日；发布日期：2020年8月14日

摘要

本文对链复形和链映射组成的短正合列进行研究。在短正合列上定义了同调序列的边缘同态，证明了它的合理性。利用链复形和链映射组成的短正合列和所定义的边缘同态，引出了正合同调序列和同调序列的自然性，并给出了证明。

关键词 :短正合列，链复形，同调序列

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

正合列是非常有用的概念，在数学研究中，是非常有用的工具。本文对链复形和链同态条件下的短正合列的性质进行讨论 [1] [2] [3] [4]，在链复形和链映射的短正合列

$0 \to C \overset{f}{\to} D \overset{g}{\to} E \to 0$ ,

对每个维数q，定义了一个边缘同态 $\partial_{*} : H_{q} (E) \to H_{q - 1} (C)$ ，先证明该边缘同态定义的合理性。由所定义的边缘同态，进一步介绍链复形和链映射的短正合列的同调性质，给出正合同调序列和同调序列自然性的证明。

2. 短正合列

为了研究短正合列的相关性质，我们先引出以下一些定义 [1] [5]。

定义2.1 [1] 如果 $\ker (g) = i m (f)$ ，则由Abel群和同态组成的序列

$C \overset{f}{\to} D \overset{g}{\to} E$

在D处正合。如果它在每个Abel群处正合，则由Abel群和同态组成的序列

$\dots \to D_{i - 1} \overset{φ_{i - 1}}{\to} D_{i} \overset{φ_{i}}{\to} D_{i + 1} \to \dots$

是一个正合序列。

定义2.2 一个链复形是一串Abel群 $C_{q}$ 和一串同态 $\partial_{q} : C_{q} \to C_{q - 1}$ ，排成一个序列

$\dots \to C_{q + 1} \overset{\partial_{q + 1}}{\to} C_{q} \overset{\partial_{q}}{\to} C_{q - 1} \overset{\partial_{q - 1}}{\to} C_{q - 2} \to \dots$

对每个维数q，满足 $\partial_{q} \circ \partial_{q + 1} = 0$ 。

定义2.3 [2] 如果对每个维数q，Abel群和同态组成的序列

$C_{q} \overset{f_{q}}{\to} D_{q} \overset{g_{q}}{\to} E_{q}$

都在 $D_{q}$ 处正合，则由链复形和链映射组成的序列

$C \overset{f}{\to} D \overset{g}{\to} E$

在D处正合。

定义2.4 设 $C = {C_{q}, \partial_{q}}$ 为链复形，那么商群

$H_{q} (C) : = \frac{\ker \partial_{q}}{i m \partial_{q + 1}}$

称为C的同调群，它的元素称为C的同调类。

定义2.5 [1] 设由链复形和链映射组成的短正合列

$0 \to C \overset{f}{\to} D \overset{g}{\to} E \to 0$ 。

对每个维数q，我们来定义一个边缘同态 $\partial_{*} : H_{q} (E) \to H_{q - 1} (C)$ 。

考察下面的交换图表(图1)

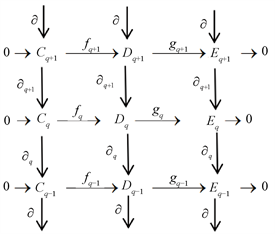
Figure 1. Chain complex and chain mapping commutative graph

图1. 链复形和链映射交换图

交换图表的每个横行都是正合序列。对于 $e_{q} \in Z_{q} (E)$ ，定义

$\partial_{*} : H_{q} (E) \to H_{q - 1} (C)$ , $[e_{q}] \mapsto [f_{q - 1}^{- 1} \partial_{q} g_{q}^{- 1} (e_{q})]$ . (1)

根据图像的交换性，且每个横行是正合序列，通过在交换图上追踪，在(1)式中，可以得到

1) 需要取逆像的地方都能取得；

2) 逆像不唯一的地方，最后结果跟逆像的选取没有关系；

3) 在同调类 $[e_{q}]$ 中取不同的代表闭链 $e_{q}$ ，所得最后结果相同。

下面我们来证明这个定义的合理性：

证明：1) 由定义可得，

$\partial_{*} : H_{q} (E) \to H_{q - 1} (C)$ ,

假定 $e_{q} \in E_{q}$ ，则 $\partial_{q} e_{q} = 0$ 。

因为 $g_{q}$ 是满射，所以存在 $d_{q} \in D_{q}$ ，使得 $g_{q} d_{q} = e_{q}$ 。

下面证明 $\partial_{q} d_{q} \in D_{q - 1}$ ，根据交换性，可得

$g_{q - 1} \partial_{q} d_{q} = \partial_{q} g_{q} d_{q} = \partial_{q} e_{q} = 0$ ,

所以

$\partial_{q} d_{q} \in \ker g_{q - 1} = i m f_{q - 1}$ .

因为 $f_{q - 1}$ 是单射，所以存在唯一的 $c_{q - 1} \in C_{q - 1}$ ，使得

$f_{q - 1} c_{q - 1} = \partial_{q} d_{q}$ .

所以 $f_{q - 1}^{- 1} \partial_{q} g_{q}^{- 1} (e_{q})$ 有意义，则

$[e_{q}] \mapsto [f_{q - 1}^{- 1} \partial_{q} g_{q}^{- 1} (e_{q})]$

是合理的定义。

2) 令 $g_{q} {d^{'}}_{q} = e_{q}$ ，其中 ${d^{'}}_{q} \in D_{q}$ ，则

$g_{q} (d_{q} - {d^{'}}_{q}) = g_{q} d_{q} - g_{q} {d^{'}}_{q} = e_{q} - e_{q} = 0$ ,

所以 $d_{q} - {d^{'}}_{q} \in \ker g_{q} = i m f_{q}$ 。则存在 $c_{q} \in C_{q}$ ，使得 $f_{q} c_{q} = d_{q} - {d^{'}}_{q}$ 。

根据交换性，可得

$f_{q - 1} \partial_{q} c_{q} = \partial_{q} f_{q} c_{q} = \partial_{q} (d_{q} - {d^{'}}_{q}) = \partial_{q} d_{q} - \partial_{q} {d^{'}}_{q}$ .

所以

$f_{q - 1}^{- 1} \partial_{q} d_{q} - f_{q - 1}^{- 1} \partial_{q} {d^{'}}_{q} = \partial_{q} c_{q} \in B_{q - 1} (C)$ ,

则 $f_{q - 1}^{- 1} \partial_{q} d_{q} + B_{q - 1} (C) = f_{q - 1}^{- 1} \partial_{q} {d^{'}}_{q} + B_{q - 1} (C)$ ，得证。

3) 假定 ${e^{'}}_{q} = \partial_{q + 1} e_{q + 1}$ ， $e_{q + 1} \in E_{q + 1}$ 。设 $g_{q + 1} d_{q + 1} = e_{q + 1}$ ，其中 $d_{q + 1} \in D_{q + 1}$ 。

根据交换性，可得

$g_{q} \partial_{q + 1} d_{q + 1} = \partial_{q + 1} g_{q + 1} d_{q + 1} = \partial_{q + 1} e_{q + 1} = e_{q}$ .

由此，可以证明边缘同态 $\partial_{*}$ 是良定义的。

定理2.6 [2] 设有链复形和链映射的短正合列

$0 \overset{}{\to} C \overset{f}{\to} D \overset{g}{\to} E \overset{}{\to} 0$ ,

则有长的正合同调序列

$\dots \to H_{q + 1} (E) \overset{\partial_{*}}{\to} H_{q} (C) \overset{f_{*}}{\to} H_{q} (D) \overset{g_{*}}{\to} H_{q} (E) \overset{\partial_{*}}{\to} H_{q - 1} (C) \to \dots$ . (2)

证明：(A) 在 $H_{q} (E)$ 处的正合性：

(A1) 设 $d_{q} \in Z_{q} (D)$ 。则

$\partial_{*} g_{*} [d_{q}] = \partial_{*} [g_{q} (d_{q})] = [f_{q - 1}^{- 1} \partial_{q} g_{q}^{- 1} g {}_{q}{(d_{q})}] = [f_{q - 1}^{- 1} \partial_{q} (d_{q})] = [f_{q - 1}^{- 1} (0)] = [0]$ .

所以 $i m g_{*} \subset \ker \partial_{*}$ 。

(A2) 设 $e_{q} \in Z_{q} (E)$ ，且 $\partial_{*} [e_{q}] = 0$ ，则有 $c_{q} \in C_{q}$ ，使得

$f_{q - 1}^{- 1} \partial_{q} g_{q}^{- 1} (e_{q}) = \partial_{q} (c_{q})$ .

取 $d_{q} = g_{q}^{- 1} (e_{q}) - f_{q} (c_{q})$ ，则

$\partial_{q} (d_{q}) = f_{q - 1} \partial_{q} (c_{q}) - \partial_{q} f_{q} (c_{q}) = 0$ ,

即 $d_{q} \in Z_{q} (D)$ 。

而 $g_{*} [d_{q}] = [g_{q} d_{q}] = [e_{q} - g_{q} f_{q} (c_{q})] = [e_{q}]$ ，所以 $\ker \partial_{*} \subset i m g_{*}$ 。

所以 $\ker \partial_{*} = i m g_{*}$ ，得证。

(B) 在 $H_{q} (D)$ 处的正合性：

(B1) 设 $c_{q} \in Z_{q} (C)$ ，则

$g_{*} f_{*} [c_{q}] = {(g \cdot f)}_{*} [c_{*}] = {(0)}_{*} [c_{q}] = 0$ ,

所以 $i m f_{*} \subset \ker g_{*}$ 。

(B2) 设 $d_{q} \in Z_{q} (D)$ ，且 $g_{*} [d_{q}] = 0$ 。

则 $\exists e_{q + 1} \in E_{q + 1}$ ，使得 $g_{q} d_{q} = \partial_{q + 1} e_{q + 1}$ 。

由于 $g_{q + 1}$ 是满射的，所以至少 $\exists$ 一个 $d_{q + 1} \in D_{q + 1}$ ，使得

$e_{q + 1} = g_{q + 1} d_{q + 1}$ ,

所以

$g_{q} d_{q} = \partial_{q + 1} e_{q + 1} = \partial_{q + 1} g_{q + 1} d_{q + 1} = g_{q} \partial_{q + 1} d_{q + 1}$ .

因为 $g_{q}$ 是链映射，所以 $g_{q} (d_{q} - \partial_{q + 1} d_{q + 1}) = 0$ 。

根据正合性，存在 $c_{q} \in C_{q}$ ，使得 $f_{q} c_{q} = d_{q} - \partial_{q + 1} d_{q + 1}$ ，所以

$f_{q - 1} \partial_{q} c_{q} = \partial_{q} f_{q} c_{q} = \partial_{q} d_{q} - \partial_{q} \partial_{q} d_{q} = 0$ .

又因为 $f_{q}$ 是单射，所以 $\partial_{q} c_{q} = 0$ ，则 $f_{*} ([c_{q}]) = [f_{q} c_{q}] = [d_{q} - \partial_{q + 1} d_{q + 1}] = [d_{q}]$ 。

由此可得， $\ker g_{*} \subset i m f_{*}$ ，

所以 $\ker g_{*} = i m f_{*}$ ，得证。

(C1) 设 $e_{q + 1} \in Z_{q + 1} (E)$ ，则

$f_{*} \partial_{*} [e_{q + 1}] = f_{*} [f_{q}^{- 1} \partial_{q + 1} g_{q + 1}^{- 1} (e_{q + 1})] = [f_{q} f_{q}^{- 1} \partial_{q + 1} g_{q + 1}^{- 1} (e_{q + 1})] = [\partial_{q + 1} g_{q + 1}^{- 1} (e_{q + 1})] = 0$ ,

所以 $i m \partial_{*} \subset \ker f_{*}$ 。

(C2) 设 $c_{q} \in Z_{q} (C)$ ，且 $f_{*} [c_{q}] = 0$ ，则存在 $d_{q + 1} \in D_{q + 1}$ ，使得

$f_{q} c_{q} = \partial_{q + 1} d_{q + 1} = e_{q + 1}$ ,

所以

$\partial_{*} [e_{q + 1}] = [f_{q}^{- 1} \partial_{q + 1} g_{q + 1}^{- 1} g_{q + 1} d_{q + 1}] = [f_{q}^{- 1} \partial_{q + 1} d_{q + 1}] = [f_{q}^{- 1} f_{q} c_{q}] = [c_{q}]$ ,

所以 $c_{q} \in i m \partial_{*}$ ，则 $\ker f_{*} \subset i m \partial_{*}$ 。

所以 $\ker f_{*} = i m \partial_{*}$ ，得证。

定理2.7 [2] 设有链复形和链映射的交换图表

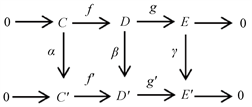
其中两个横行都是链复形的短正合列。则它们的正合同调序列之间有交换图表

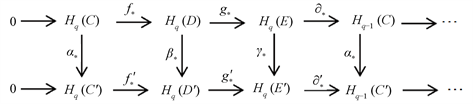
证明：行的正合性是定理2.6已证明，下面我们来证明列的正合性，先画出以下交换图表(图2)：

1) 如果 $[e_{q}] \in H_{q} (E)$ ，则需证明 $α_{*} \partial_{*} [e_{q}] = {\partial^{'}}_{*} γ_{*} [e_{q}]$ 。

因为g是满射的，所以存在 $d_{q} \in D_{q}$ ，使得

$g_{q} (d_{q}) = e_{q}$ .

$\partial_{*} [e_{q}] = [f_{q - 1}^{- 1} \partial_{q} g_{q}^{- 1} (e_{q})] = [f_{q - 1}^{- 1} \partial_{q} g_{q}^{- 1} g_{q} (d_{q})] = [f_{q - 1}^{- 1} \partial_{q} (d_{q})]$ ,

Figure 2. Chain complex and chain homomorphism three-dimensional commutative graph

图2. 链复形和链同态三维交换图

所以 $f_{q - 1}^{- 1} \partial_{q} (d_{q}) = c_{q - 1}$ ，则 $f_{q - 1} (c_{q - 1}) = \partial_{q} (d_{q})$ ，其中 $c_{q - 1} \in C_{q - 1}$ 。

$α_{*} \partial_{*} [e_{q}] = [α_{q - 1} f_{q - 1}^{- 1} \partial_{q} (d_{q})] = [α_{q - 1} (c_{q - 1})]$ ,

因为 $γ$ 是链映射，所以

${g^{'}}_{q} β_{q} (d_{q}) = γ_{q} g_{q} (d_{q}) = γ_{q} (e_{q})$ ,

所以

${\partial^{'}}_{*} [γ_{q} (e_{q})] = [f_{q - 1}^{- 1} {\partial^{'}}_{q} {g^{'}}_{q}^{- 1} {g^{'}}_{q} β_{q} (d_{q})] = [f_{q - 1}^{- 1} {\partial^{'}}_{q} β_{q} (d_{q})] = [{c^{'}}_{q - 1}]$ ,

其中 ${c^{'}}_{q - 1} \in {C^{'}}_{q - 1}$ 。

则 ${f^{'}}_{q - 1} ({c^{'}}_{q - 1}) = {\partial^{'}}_{q} β_{q} (d_{q})$ ，因此，

${f^{'}}_{q - 1} α_{q - 1} (c_{q - 1}) = β_{q - 1} f_{q - 1} (c_{q - 1}) = β_{q - 1} \partial_{q} (d_{q}) = {\partial^{'}}_{q} β_{q} (d_{q}) = {f^{'}}_{q - 1} ({c^{'}}_{q - 1})$ ,

又由于 ${f^{'}}_{q - 1}$ 是单射，所以 $α_{q - 1} (c_{q - 1}) = {c^{'}}_{q - 1}$ 。

所以 $α_{*} \partial_{*} [e_{q}] = {\partial^{'}}_{*} γ_{*} [e_{q}]$ 。

2) 因为 $\partial_{q + 1} (d_{q + 1}) = d_{q}$ ，根据交换性，可得

$γ_{q} g_{q} (d_{q}) = γ_{q} g_{q} \partial_{q + 1} (d_{q + 1}) = γ_{q} \partial_{q + 1} g_{q + 1} (d_{q + 1}) = \partial_{q + 1} γ_{q + 1} g_{q + 1} (d_{q + 1}) = \partial_{q + 1} ({e^{'}}_{q + 1})$ ,

$γ_{*} g_{*} [d_{q}] = [γ_{q} g_{q} (d_{q})]$ ,

$\partial_{q} γ_{q} g_{q} (d_{q}) = γ_{q - 1} \partial_{q} g_{q} (d_{q}) = γ_{q - 1} g_{q - 1} \partial_{q} (d_{q}) = 0$ ,

所以

$[{g^{'}}_{q} β_{q} (d_{q})] = [γ_{q} g_{q} (d_{q})]$ .

3. 结论

本文对链复形和链同态条件下的短正合列的性质进行讨论。首先，给出了边缘同态 $\partial_{*}$ 的定义，通过对交换图表进行追踪，证明了其定义的合理性。然后，证明了由短正合列诱导的长正合同调序列和边缘同态 $\partial_{*}$ 的自然性。短正合列还有其他问题需要进行研究，它是一个很有用的数学工具，在数学研究方面起到很重要的作用。如正合序列还有一个妙用“五引理”，这也是“图上追踪法”的一个典型例子。

文章引用

范宏涛. 短正合列的性质
The Nature of Short Exact Sequence[J]. 理论数学, 2020, 10(08): 719-725. https://doi.org/10.12677/PM.2020.108085

参考文献

1. 姜伯驹. 同调论[M]. 北京: 北京大学出版社, 2006.

2. Rotman, J.J. (2010) Advanced Modern Algebra: Second Edition. American Mathematical Society, Rhode Island.

3. 陈家鼐. 环与模[M]. 北京: 北京师范学院出版社, 1989.

4. Scott Osborne, M. (2000) Basic Homological Algebra. Springer-Verlag, New York.

5. 赵春来, 徐明曜. 抽象代数[M]. 北京大学出版社, 2008.

期刊菜单