辽宁师范大学数学学院,辽宁 大连
收稿日期:2024年1月22日;录用日期:2024年3月14日;发布日期:2024年3月21日

摘要
随着二维Zinbiel代数,预李代数分类结果的完成,在转置泊松代数的研究基础上,本文研究了二维转置预泊松代数的分类以及转置预泊松代数与转置泊松代数的关系。首先利用二维Zinbiel代数的分类结果,取定转置预泊松代数上的Zinbiel代数,计算在这个条件下二维转置预泊松代数上预李代数的左乘运算,确定预李代数的类型。通过具体计算讨论二维的转置预泊松代数在同构意义下的分类。
关键词
转置预泊松代数,预李代数,Zinbiel代数

Classification of 2-Dimensional Transposed Pre-Poisson Algebras
Xueting Yang
School of Mathematics, Liaoning Normal University, Dalian Liaoning
Received: Jan. 22nd, 2024; accepted: Mar. 14th, 2024; published: Mar. 21st, 2024

ABSTRACT
With the completion of the classification of 2-dimensional Zinbiel algebras and pre-lie algebras, based on the study of transposed Poisson algebras, in this paper, the classification of two-dimensional transposed pre-poisson algebras and the relationship between transposed pre-poisson algebras and transposed Poisson algebras are studied. First, by using the classification results of 2-dimensional Zinbiel algebras, we determine the Zinbiel algebras on transposed pre-poisson algebras, under these conditions, the left multiplication of pre-Lie algebras on two-dimensional transposed pre-poisson algebras is calculated, and the type of pre-Lie algebras is determined. The classification of two-dimensional transposed pre-poisson algebras in isomorphic sense is discussed by concrete calculation.
Keywords:Transposed Pre-Poisson Algebra, Pre-Lie Algebra, Zinbiel Algebra

Copyright © 2024 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
预李代数也称为左对称代数,是一类非结合代数。是由Gerstenhaber在研究结合环的上同调结构中提出的 [1] ,它在几何和代数的理论中有着广泛的应用。Zinbiel代数是Loday在文献 [2] 中引入的。Aguiar在 [3] 中通过将Zinbiel代数与预李代数结合在一起,满足一些相容条件后,引入了预泊松代数,本文将通过类似方法引入转置预泊松代数的概念。转置预泊松代数与转置泊松代数之间有着一定联系,转置泊松代数是文献 [4] 中作者通过交换泊松代数的莱布尼茨规则中两个二元运算引入的,它也是当下研究的重要课题。在文献 [5] 中作者给出了转置泊松代数的分类。本文将研究转置泊松代数和转置预泊松代数的联系,并研究二维转置预泊松代数在同构意义下的分类。
2. 预备知识
定义2.1 [4] 设A是复数域上的向量空间,
是A上的双线性运算,若
是交换结合代数,
是李代数,且满足相容条件
,(2.1)
则称
为转置泊松代数。
定义2.2 [2] 设A是复数域上的向量空间,且有双线性运算
,若
满足
, (2.2)
则称
为Zinbiel代数。
定义2.3 [6] 设
是交换结合代数,V是线性空间,
是A到
的线性映射,若满足
, (2.3)
则称
是交换结合代数
的表示。
命题2.1设
是Zinbiel代数,
为A关于
的左乘运算,在A上定义
, (2.4)
则
(1)
为交换结合代数;
(2)
是交换结合代数
的表示。
证(1). 由(2.4)式知,
则
为交换代数。
任取
,下面验证
是否成立,由
和
运算满足 式,直接计算可知
,
.
由
是Zinbiel代数,可知
满足 式,故
,则
为结合代数。
综上可知,
为交换结合代数。
(2). 由(1)知
为交换结合代数,设
为A关于
的左乘运算,则对
,有
,
,
由
是Zinbiel代数,可知
满足(2.2)式,故
满足(2.3)式,根据定义1.3可知
是交换结合代数
的表示。
定义1.4 [1] 设A是复数域上的向量空间,且有双线性运算
,若
满足
, (2.5)
则称
为预李代数。
命题2.2 [7] [8] 设A是预李代数,
为A关于
的左乘运算,在A上定义
,
则
(1)
为李代数;
(2)
是李代数
的表示。
定理2.1 [9] 若为二维Zinbiel代数,则存在的一组基
,满足
。
定理2.2 [10] 设是复数域上的二维左对称代数,则一定同构于下面的(互不同构)左对称代数:
定义2.5 [11] 设
是一个转置泊松代数,V是线性空间,
是A到
的线性映射,若有
是交换结合代数
表示,
是李代数
的表示,且满足
其中
,则称
是转置泊松代数
的表示。
3. 转置预泊松代数与转置泊松代数的关系
定义3.1设A是向量空间,
是A上的双线性运算,若
是Zinbiel代数,
是预李代数,且满足
, (3.1)
, (3.2)
其中
,则称
为转置预泊松代数。
定理3.1设
为转置预泊松代数。在A上定义
,
则
是转置泊松代数。
证由
为转置预泊松代数,可知
是Zinbiel代数,
是预李代数,根据命题1.1的(1)可知
是交换结合代数,根据命题2.2的(1)可知
是李代数。
由定义3.1知,对
,
满足(3.1)与(3.2)式,直接计算得
可知
满足 式,故
是转置泊松代数。
设
为转置预泊松代数,用
分别表示A关于
的左乘运算,即
.
定理3.2设
是转置预泊松代数,在A上定义
,
则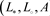 是转置泊松代数
的表示。
是转置泊松代数
的表示。
证根据定理2.1知 是转置泊松代数。由
为Zinbiel代数,则根据命题2.1的(2)可知
是交换结合代数
的表示,由
为预李代数,根据命题2.2的(2)可知
是李代数
的表示。
是转置泊松代数。由
为Zinbiel代数,则根据命题2.1的(2)可知
是交换结合代数
的表示,由
为预李代数,根据命题2.2的(2)可知
是李代数
的表示。
再由
是转置预泊松代数,根据定理3.1可知在A上有(3.1)式成立,对
,则有
即
满足等式(2.6)。
同时,在A上有(3.2)式成立,因此
即
满足等式(2.7)。
综上所述可知
是转置泊松代数
的表示。
定义3.2设
与
是转置预泊松代数,
为线性映射,若
满足
,
则称
为
到
的同态映射。
特别地,若
为双射,则称
为
和
的同构映射. 显然,若两个转置预泊松代数
和
同构,则作为Zinbiel代数,
和
同构,作为预李代数,
和
同构。
4. 二维转置预泊松代数上关于预李代数的左乘运算
定理4.1设
是二维转置预泊松代数,则存在A的一组基
,使得
,且
其中
,且
,
。
证设
是二维转置预泊松代数,由定理2.1知,存在A的一组基
,满足
. 从而
关于
的左乘运算在
下对应的矩阵为:
设
在
下对应的矩阵为
,
根据转置预泊松代数的定义,由(3.1),(3.2)式知,对
,关于
的左乘运算需满足
(4.1)
(4.2)
对(4.1)式考虑
分别取
的情况:
(a) 若
,则有
即
则有
(b) 若
,则有
即
故对任意
,等式恒成立。
(c) 若
,则有
即
计算得
。
(d)
,则有
即
,故等式左右两端都为0,等式恒成立。
对(4.2)式考虑
分别取
的情况:
(a) 若
或
,则
显然等式左右两端都为0,等式恒成立。
(b) 若
,则
即
,
此时,等式恒成立。
(c) 若
,则
,
即
,
此时,等式恒成立。
此外,根据预李代数的定义,由(1.3)式知,对
,A关于
的运算需要满足条件:
. (4.3)
对(4.3)式考虑
分别取
的情况:
(a) 若
或
,则有
,
显然等式左右两端都为0,等式恒成立。
(b) 若
,则
即
计算得
。
(c) 若
,则
即
计算得
。
综上所述,得
取
,则有
,
其中
,且
,
。
5. 二维转置预泊松代数的类型
定理5.1设
是二维转置预泊松代数,则存在A的基
,使
,此时
中的运算
取以下几种类型:
(1)
,
同构于A4型的预李代数。
(2)
,
同构于A5型的预李代数。
(3)
,
同构于A8型的预李代数。
(4)
,
同构于A9型的预李代数。
(5)
,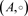 同构于A7型的预李代数。
同构于A7型的预李代数。
(6)
,
同构于A7型的预李代数。
证明:设
是二维转置预泊松代数,由定理1.1知,存在A的一组基
使得
,且根据定理3.1知,
中关于
的运算为:
,
其中
,且
,
。下面进行分情况讨论。
<1> 若
,由
,可知
,此时
,
下面讨论
的取值:
(a) 若
,则
此时
同构于A4型的预李代数。
(b) 若
,则
作非退化线性替换
,则
此时
同构于A5型的预李代数。
(c)
,则有
作非退化线性替换
,则
此时
同构于A8型的预李代数。
(d)
,则有
作非退化线性替换
,则
此时
同构于A9型的预李代数。
<2> 若
,由
可知
,再由
可知
,此时
,
下面讨论
的取值:
(a) 若
,则有
作非退化线性替换
,则
此时
同构于A7型的预李代数。
(b) 若
,则有
作非退化线性替换
,则
此时
同构于A7型的预李代数。
6. 二维转置预泊松代数在同构意义下的分类
定理6.1设
是二维转置预泊松代数,
为A的一组基,则
在同构意义下有以下6种:
(1)
;
(2)
;
(3)
;
(4)
;
(5)
;
(6)
。
其中,
,且
。
证设
是二维转置预泊松代数。由定理5.1知A关于
的运算有6种情况,且定理5.1中(1),(2),(3),(4)和(5),(6)对应的预李代数互相不同构,因此其对应的转置预泊松代数也互相不同构,此时只需考虑定理5.1中的(5),(6)两种转置预泊松代数是否同构。
设
为定理5.1中第(5)种转置预泊松代数,取
为满足定理5.1中第(5)种转置预泊松代数
的一组基;
为定理5.1中第(6)种转置预泊松代数,取
为满足定理5.1中第(6)种转置预泊松代数
的一组基。
用反证法,若(5),(6)两种转置预泊松代数同构,f为其同构映射,则f为
到
的可逆线性变换,满足
.
设线性变换f在基
下的矩阵为
,其中
,即
.
一方面,f是Zinbiel代数
到
上的同构映射,因此f需满足:
,
,
,
.
计算可得
。此时
.
另一方面,f为预李代数
到
的同构需要满足以下4个方程:
,
 ,
,
,
.
直接计算可知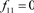 。此时
,故F不可逆,可知f不是同构映射,即
,
不同构。
。此时
,故F不可逆,可知f不是同构映射,即
,
不同构。
7. 总结与展望
本文通过将Zinbiel代数与预李代数结合在一起,满足特定相容条件后,引入了转置预泊松代数概念,讨论转置泊松代数与转置预泊松代数的关系,再根据二维Zinbiel代数,预李代数的分类结果,通过具体计算讨论二维转置预泊松代数在同构意义下的分类。
代数分类问题对数学,物理以及其他领域都有重要作用。在本文研究基础上,可继续进行三维转置预泊松代数的分类研究。
文章引用
杨雪婷. 二维转置预泊松代数的分类
Classification of 2-Dimensional Transposed Pre-Poisson Algebras[J]. 理论数学, 2024, 14(03): 32-41. https://doi.org/10.12677/PM.2024.143083
参考文献
- 1. Gerstenhaber, M. (1963) The Cohomology Structure of an Associative Ring. Annals of Mathematics, 78, 267-288.
https://doi.org/10.2307/1970343
- 2. Loday, J.-L. (1995) Cup Product for Leibniz Cohomology and Dual Leibniz Algebras. Mathematica Scandinavica, 77, 189-196. https://doi.org/10.7146/math.scand.a-12560
- 3. Aguiar, M. (2000) Pre-Poisson Algebras. Letters in Mathematical Physics, 54, 263-277.
https://doi.org/10.1023/A:1010818119040
- 4. Bai, C., Bai, R., Guo, L. and Wu, Y. (2023) Transposed Poisson Algebras, Novikov-Poisson Algebras, and 3-Lie Algebras. Journal of Algebra, 632, 535-566. https://doi.org/10.1016/j.jalgebra.2023.06.006
- 5. Beites, D.P., Ouaridi, F.A. and Kaygorodov, I. (2023) The Al-gebraic and Geometric Classification of Transposed Poisson Algebras. Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas, 117, Article Number 55. https://doi.org/10.1007/s13398-022-01385-4
- 6. Liu, G. and Bai, C. (2023) New Splittings of Operations of Poisson Algebras and Transposed Poisson Algebras and Related Algebraic Structures. arXiv:2310.08299v1
- 7. Aguiar, M. (2000) Pre-Poisson Algebras. Letters in Mathematical Physics, 54, 263-277.
https://doi.org/10.1023/A:1010818119040
- 8. Bai, C. (2008) Left-Symmetric Bialgebras and an Analogue of the Classical Yang-Baxter Equation. Communications in Contemporary Mathematics, 10, 221-260. https://doi.org/10.1142/S0219199708002752
- 9. Dzhumadil’Daev, A.S. and Tulenbaev, K.M. (2005) Nilpotency of Zinbiel Algebras. Journal of Dynamical and Control Systems, 11, 195-213. https://doi.org/10.1007/s10883-005-4170-1
- 10. 白承铭, 孟道骥. 二维左对称代数的分类[J]. 科学通报, 1996(23): 2207.
- 11. Liu, G. and Bai, C. (2023) A Bialgebra Theory for Transposed Poisson Algebras via An-ti-pre-LieBialgebras and Anti-pre-Lie-Poisson Bialgebras. arXiv:2309.16174v1






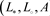 是转置泊松代数
的表示。
是转置泊松代数
的表示。 是转置泊松代数。由
为Zinbiel代数,则根据命题2.1的(2)可知
是交换结合代数
的表示,由
为预李代数,根据命题2.2的(2)可知
是李代数
的表示。
是转置泊松代数。由
为Zinbiel代数,则根据命题2.1的(2)可知
是交换结合代数
的表示,由
为预李代数,根据命题2.2的(2)可知
是李代数
的表示。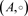 同构于A7型的预李代数。
同构于A7型的预李代数。 ,
,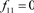 。此时
,故F不可逆,可知f不是同构映射,即
,
不同构。
。此时
,故F不可逆,可知f不是同构映射,即
,
不同构。