Applied Physics
Vol.
10
No.
09
(
2020
), Article ID:
37658
,
6
pages
10.12677/APP.2020.109054
地磁场发电机Rossler模型的混沌分析与数值仿真
张熙,王贺元
沈阳师范大学,数学与系统科学学院,辽宁 沈阳

收稿日期:2020年8月28日;录用日期:2020年9月10日;发布日期:2020年9月17日

摘要
本文根据混沌理论分析方法,讨论了地磁场发电机Rossler模型的产生混沌现象的参数值,并据此进行数值仿真。讨论了Rossler模型的耗散性以及吸引子的存在性;系统的平衡点及其在给定参数值下的局部稳定性;利用MATLAB进行数值仿真作图,从分岔图、最大Lyapnov指数图、吸引子图等各个指标说明结论的正确性。
关键词
地磁场发电机,Rossler模型,混沌,MATLAB
Chaos Analysis and Numerical Simulation of Geomagnetic Field Generator Rossler Model
Xi Zhang, Heyuan Wang
School of Mathematics and System Science, Shenyang Normal University, Shenyang Liaoning
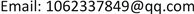
Received: Aug. 28th, 2020; accepted: Sep. 10th, 2020; published: Sep. 17th, 2020

ABSTRACT
In this paper, the parameter values of Rossler model for geomagnetic field generator are discussed and numerical simulation is carried out. The dissipation of Rossler model and the existence of attractors are discussed. The equilibrium point of the system and its local stability under the given parameter value; MATLAB numerical simulation is used to illustrate the correctness of the conclusion from the bifurcation diagram, maximum Lyapnov index diagram, attractor diagram and other indicators.
Keywords:Geomagnetic Field Generator, Rossler Model, Chaos, MATLAB

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
自从1963年气象学家E. N. Lorenz发现了Lorenz系统 [1],并首次用简单的三维常系数微分方程组描述其混沌行为,人们在许多不同的领域发现了混沌的存在,并建立许多的数学模型来描述这些混沌现象 [2]。
在地磁学中,混沌有较为广泛的应用。Rossler模型就是其中杰出的代表,它是由德国物理化学家O. E. Rossler在地磁场发电机的背景下发现的,是一种可以从Lorenz系统中提取出来的具有非对称吸引子的非线性动力系统 [3]。
Rossler系统结构简单,却具有非常复杂的混沌特性,通过数值模拟,可以观察到系统出现丰富的复杂动态,包括周期、拟周期和混沌等现象。由于Rossler系统具有良好的混沌性质,经典的非线性动力学文献 [3] 中,曾将其作为连续型混沌系统的例子加以说明,并指出可以利用与Lorenz系统相似的方法进行研究。本文仿照Lorenz系统的分析过程,讨论了Rossler系统的基本性质、平衡点及其局部稳定性,并对其进行初步的数值仿真分析。
2. 数学模型
2.1. Rossler系统动力学模型
Rossler模型具有一个非线性项,可以由含参数的三维非线性常微分方程组表示 [3]:
(1)
其中a、b和c为系统参数,x、y和z为系统变量, 、 和 分别表示x、y和z关于t的一阶导数。
2.2. 耗散性及吸引子存在性
系统(1)的向量场散度为 ,当 时,系统是耗散的,并且以指数形式 收敛,收缩为体积元 ,且当 时包含系统轨线的每个小体积元以指数率
收缩到0,所有系统的轨线最终会被限制在一个体积为0的极限子集上,且渐近运动将被固定到一个吸引子上,这就说明了吸引子的存在性 [4]。
2.3. 平衡点
令
(2)
解得
(3)
故Rossler模型非对称的平衡点有两个,分别为:
(4)
2.4. 局部稳定性
系统(1)对应的雅各比矩阵为
(5)
可以计算出其对应的特征多项式 [5] [6] 为
(6)
当 , 时,经过计算得, ,,,,,,故该系统存在两个平衡点,其坐标为 ,。
点对应的特征方程为
(7)
解得的三个特征根为 ,,。容易看出, ,,故此时 点不是稳定的平衡点 [7] [8]。
点对应的特征方程为
(8)
解得的三个特征根为 ,,。容易看出, ,,故此时 点不是稳定的平衡点。即此时系统正处于混沌状态。
3. Rossler系统的数值仿真分析
为直观探究Rossler系统的混沌行为,本节选取MATLAB软件利用龙格–库塔法进行数值仿真 [9]。为印证上一节中,当 , 时系统正处于混沌状态的结论,如图1所示,固定参数 ,,绘制系统(1)的吸引子图 [10]。
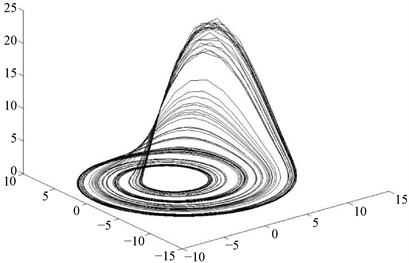
Figure 1. When ,, the attractor diagram of system (1)
图1. 当 , 时,系统(1)的吸引子图
在图1中,系统(1)的轨线被平衡点排斥,但不能无限延伸,最终仍回到平衡点所在的控制区域中,又被平衡点排斥,以此循环往复。轨线整体看起来井然有序又杂乱无章,此时系统(1)处于混沌状态。
如图2所示,对系统(1)令参数 ,令参数c在区间 上进行变化,绘制分岔图。

Figure 2. When ,, the bifurcation diagram of the system (1)
图2. 当 , 时,系统(1)的分岔图
由分岔图可知,该系统对于参数c是阵发性混沌,混沌发生一段时间后进入周期窗口,然后经历分岔重新进入混沌。当c > 4以后,系统就处于混沌状态。
如图3所示,对系统(1)令参数 ,,令参数b在区间 上进行变化,绘制分岔图。
Figure 3. When ,,, the bifurcation diagram of the system (1)
图3. 当 ,, 时,系统(1)的分岔图
从图像中可以看出系统(1)对于参数b是阵发性混沌,当 , 时,系统正处于混沌态。
4. 结论
地磁场发电机Rossler模型是一种自治混沌系统,该系统具有一个非线性项,但仍然能够产生混沌现象。Rossler系统是耗散系统,且存在非对称的两个平衡点。当系统参数 , 时,两个平衡点所对应的雅各比矩阵特征值均存在正值,两个平衡点都是不稳定的平衡点。对Rossler系统进行数值仿真分析,绘制吸引子图和分岔图的结果显示,当系统参数 , 时,两个系统正处于混沌状态。
文章引用
张 熙,王贺元. 地磁场发电机Rossler模型的混沌分析与数值仿真
Chaos Analysis and Numerical Simulation of Geomagnetic Field Generator Rossler Model[J]. 应用物理, 2020, 10(09): 408-413. https://doi.org/10.12677/APP.2020.109054
参考文献
- 1. Lorenz, E.N. (1963) Deterministic Nonperiodic Fiow. Journal of the Almospheric Sciences, 20, 130-141. https://doi.org/10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2
- 2. Li, T.Y. and Yorke, J.A. (1975) Period Three Implies Chaos. The American Mathematical Monthly, 82, 985-992. https://doi.org/10.1080/00029890.1975.11994008
- 3. 郝柏林. 分岔、混沌、奇怪吸引子、湍流及其它——关于确定系统中的内在随机性[J]. 物理学进展, 1983, 3(3): 335-416.
- 4. 彭建奎, 俞建宁, 张莉, 等. 一个新混沌系统的混沌分析及混沌控制[J]. 河北大学学报, 2008, 32(3): 1-4.
- 5. 王贺元, 崔进. 旋转流动混沌行为的全局稳定性分析及数值仿真[J]. 数学物理学报, 2017, 37(4): 785-786.
- 6. 王贺元. 非线性系统的动力学行为及其数值分析[M]. 北京: 科学出版社, 2018: 114-117.
- 7. 朱克勤, 彭杰. 高等流体力学[M]. 北京: 科学出版社, 2017: 36-42.
- 8. 刘秉正, 彭建华. 非线性动力学[M]. 北京: 高等教育出版社, 2003: 120-129.
- 9. 王贺元. 平面不可压缩磁流体动力学五模类Lorenz方程组的动力学行为及其数值仿真[J]. 数学物理学报, 2017, 37(1): 199-216.
- 10. 郭怡冰. Rossler系统的混沌控制和研究[D]: [硕士学位论文]. 西安: 西安建筑科技大学, 2010.