ABSTRACT

As a novel sampling, coding and decoding theory, compressed sensing has been a powerful tool which was widely used to the fields of image processing, pattern recognition, automatic control, biological sensors and so on. Based on the Barzilai-Borwein (B-B) gradient projection for sparse reconstruction (GPSR-BB), this paper proposed a new algorithm by using predictor-corrector technique for solving compressed sensing problem fast. In the new algorithm, a predicted point was first generated by traditional gradient projection and then a new iteration point was obtained with B-B method according to the predicted point. In our algorithm, the calculation of a single iteration is also simple, and by using predictor-corrector technique, the iteration point may be closer to the solution of the problem, thereby the number of the iteration would be reduced. Numerical results show that the running time of the new algorithm is less than GPSR-BB for some randomly generated test problems.

Keywords:Compressed Sensing, Sparse Reconstruction, Convex Optimization, Gradient Projection

一种改进的稀疏信号重构的梯度投影算法

胡剑峰

海南师范大学数学与统计学院，海南 海口

收稿日期：2017年8月22日；录用日期：2017年9月3日；发布日期：2017年9月8日

摘 要

压缩感知理论作为一种全新的信号采集、编解码理论，已被广泛地应用于图像处理、模式识别、自动控制和生物传感等领域，并展现出强大的力量。为了更快速地求解压缩感知问题，在稀疏信号重构的Barzilai-Borwein (B-B)梯度投影(Barzilai-Borwein Gradient Projection for Sparse Reconstruction, GPSR-BB)算法的基础上，采用预测校正的技巧，提出了一种改进的梯度投影算法。该算法首先由常数步长的梯度投影产生一个预测点，再根据预测点及B-B方法计算步长得到新的迭代点。新算法单步迭代计算同样简单，且采用预测校正技巧可使迭代点更接近问题的解，从而可望减少算法的总的迭代次数。对随机生成的测试问题进行数值实验，数值结果表明新算法的运行时间要少于GPSR-BB算法。

关键词 :压缩感知，稀疏重构，凸优化，梯度投影

Copyright © 2017 by author and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

在信号处理中，为了能准确地重构原始信号，由奈奎斯特(Nyquist)采样定理可知，传统的系统采样频率至少为信号带宽的两倍。而随着信息时代的高速发展，人们对信息量的需求与日俱增，因而信号的带宽越来越大，这就对传统的信号采样、存储、处理和传输提出了挑战。2006年，Donoho和Candès等几乎同时独立地提出了一种全新的信号处理技术——压缩感知(Compressed Sensing, CS)理论 [1] [2] 。CS理论与传统信号处理技术有着本质的不同。传统的信号处理技术，如奈奎斯特采样，是对信号先采样后压缩，而CS技术则是将信号或数据的采样和压缩同时进行，从而提高了效率。CS理论的基本思想是：若原始信号是稀疏的，则可利用一个测量矩阵，通过线性变换将高维的原始信号压缩成一个低维的测量信号，再由这个低维的测量信号，采用某种有效的重构算法，可以很高概率的恢复原始信号。此外，若原始信号是非稀疏的，则需要找一个正交变换，使其在该变换基矩阵下具有稀疏表示。目前关于信号稀疏表示的研究方法主要有傅里叶分析、小波分析和多尺度几何分析 [3] 等。CS一经提出，就受到广泛关注，并在图像去噪 [4] 、人脸识别 [5] 、雷达成像 [6] 、核磁共振成像 [7] 等领域取得了成功的应用。

由CS理论可知，稀疏信号重构的关键在于测量矩阵的构造和重构算法的设计。陶哲轩和Candès [8] [9] [10] 证明了当测量矩阵满足限制等距性质(Restricted Isometry Property, RIP)条件时，可通过某种重构算法恢复原始信号，并证明了部分正交矩阵满足RIP条件，而随机高斯矩阵、随机伯努利矩阵等都能以极高的概率满足该条件。最近，文 [11] [12] 又对该条件进行了改进，将其中的参数取值范围进一步放宽。

目前，压缩感知的重构算法主要可分为贪婪追踪算法和凸优化算法两大类。贪婪追踪算法包括匹配追踪算法(Matching Pursuit, MP) [13] 、正交匹配追踪算法(Orthogonal Matching Pursuit, OMP) [14] 和稀疏度自适应的匹配追踪算法(Sparsity Adaptive Matching Pursuit, SAMP) [15] 等；凸优化算法包括基追踪算法(Basis Pursuit, BP) [16] 、迭代阈值算法(Iterative Thresholding, IT) [17] 、迭代硬阈值算法(Iterative Hard Thresholding, IHT) [18] 、梯度投影算法(Barzilai-Borwein Gradient Projection for Sparse Reconstruction, GPSR-BB) [19] 、交替方向算法(Alternating Direction Method, ADM) [20] 和邻近梯度算法(Proximal Point Algorithm, PPA) [21] 等。

这两类算法各有千秋，互有长短。贪婪追踪算法是对稀疏非凸优化问题进行求解，实质上是通过局部最优化对原始稀疏信号的一个逐次逼近过程，其迭代易于理解和实现，因而倍受青睐。然而其不能保证全局收敛性，且解的精度不高。此外，匹配追踪和正交匹配追踪算法计算量最小，但需要事先知道信号的稀疏度。稀疏度自适应匹配追踪算法可以通过设置终止条件来使稀疏度自适应，但迭代次数多，运算量较大。凸优化算法是对松弛的凸优化问题进行求解，迭代的理论和计算相对复杂一些，但无需事先知道信号的稀疏度，且只需更少的测量数量就能获得更高精度的解。在众多的凸优化重构算法中，GPSR-BB算法因其迭代过程相对简单易行，求解较快，且容易实现热启动(warm-start)，而在实际应用中得到广泛的关注。本文在GPSR-BB算法的基础上，结合预测校正技术，提出了一种改进的GPSR-BB算法，即预测校正的梯度投影算法(Predictor-Corrector Gradient Projection with Barzilai-Borwein, PCGP-BB)，数值实验结果表明PCGP-BB算法比GPSR-BB算法更有效。

2. 压缩感知的凸优化模型

众所周知，CS中的稀疏信号重构问题可描述为如下稀疏优化模型：

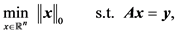(1)

其中表示向量x中非零元素的个数，为测量矩阵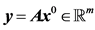，为原始稀疏信号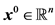经压缩后的观测值。式(1)是一个NP-hard的问题 [22] 。而Tao和Candès在文献 [9] 中指出，当测量矩阵A满足RIP条件时，式(1)等价于如下松弛的凸优化模型，即基追踪问题(Basis Pursuit Problem)

(2)

其中为x的l₁范数，它是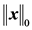的凸包络。

若观测向量y受到稠密的小的噪声(如高斯白噪声)干扰时，很自然地可将式(2)进一步松弛为如下凸优化模型：

(3)

其中为非负参数，表示向量x的l₂范数。

式(3)是一个二阶锥约束的凸优化问题，而由凸分析可知，存在，使得式(3)等价于如下混合范数最小化问题：

(4)

实质上式(4)是式(3)的Lagrange形式，其中被称为正则因子。

3. 改进的梯度投影法

式(4)是不可微的问题，不能直接采用梯度算法求解。Figueiredo, Nowak和Wright在文献 [19] 中将其转化为如下非负约束的凸二次规划问题：

(5)

其中，，，，，，，，。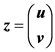

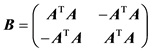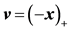求解式(5)的梯度投影法的一般迭代格式为，其中为的梯度，称为步长。文 [19] 根据前两个迭代点和采用Barzilai-Borwein方法计算步长，提出了GPSR-BB算法。GPSR-BB算法包括单调的和非单调的两种，其计算简单有效，在实际应用中表很好，尤其是非单调的GPSR-BB算法求解更为快些。然而，GPSR-BB算法对于初始点的取值很敏感，当初始点为0时，效果很好，而初始点取值不为0时，则效果不佳，甚至求解失败。而采用常数步长规则(即令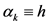，为正的常数)的梯度投影法计算最简单且不依赖于初始点的选取，但需要较多的迭代次数。因此，本文将非单调的GPSR-BB算法和常数步长的梯度投影法进行结合，并利用预测校正的技巧，先由当前迭代点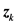采用常数步长的梯度投影法计算得到一个预测点，然后再根据和采用B-B方法计算步长，从而可得到下一个迭代点。由于采用了预测校正技术，新算法可望比GPSR-BB算法需要更少的迭代此数，从而可减少总的计算时间，且新算法对于初始点不为0时亦可成功求解。

显然是Lipschitz连续的且Lipschitz常数。因为

所以有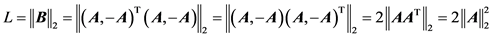。若A是行正交的，则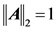有，因而有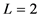。此外，由凸优化的梯度投影法的收敛性 [23] 可知，当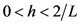时，常数步长的梯度投影法收敛，而且若式(5)是强凸的，则取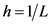时收敛最快且为线性收敛。虽然式(5)是非强凸的，但本文仍然取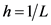进行计算。PCGP-BB算法步骤如下

步骤1：(初始化)给定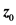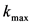，，， (迭代次数上限)，令；

步骤2：若或 收敛终止条件满足， 算法终止；

步骤3：计算预测点，，；

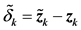步骤4：计算步长：若，则令；否则，令

步骤5：更新迭代点，令，转步骤2；

显然，PCGP-BB算法每次迭代计算的关键在于梯度和的计算。由于以及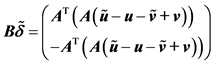，，因而可知其主要计算量为矩阵与向量的乘积运算，故而其单步迭代的计算复杂度为，与GPSR-BB算法的单步迭代计算复杂度一样，同样简单易于实现。

4. 数值结果

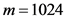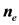在本节中，我们考虑一个典型的压缩感知问题 [19] [24] ，通过一个长度为m的测量向量y来恢复出长度为n的原始信号。其中，，原始信号包含160个随机，是方差为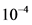和均值为零的高斯白噪声。此外，采用文献 [24] 中的建议，取，并和文献 [19] 一样，先按照独立同分布的标准高斯分布随机产生测量矩阵A，然后对其行正交化，并采用终止条件：，其中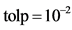。此外，我们取，，，，。

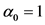在MATLAB R2013b的平台上进行数值试验，计算机是Windows 7操作系统，内存为8 GB，处理器为Intel Core i5-4460 3.20 Ghz和16位十进制精度的个人电脑。代码PCGP-BB与GPSR-BB (包括单调和非单调)分别代表预测校正的梯度投影算法和B-B步长的梯度投影算法的程序。分别用PCGP-BB与GPSR-BB求解并比较其迭代次数和CPU时间。表1和表2分别给出了初值和时，

表1. PCGP-BB和GPSR-BB的迭代次数和CPU时间(取十次的平均值，)

表2. PCGP-BB和GPSR-BB的迭代次数和CPU时间(取十次的平均值，)

PCGP-BB和GPSR-BB的迭代次数和CPU时间(以十次测试的平均值为准)，其中是Matlab随机向量生成函数。由于采用相同的最优性条件作为终止条件，这三者的均方误差基本相同，因而未在表中列出。由表1和表2可知，就所测试的问题，PCGP-BB的迭代次数和CPU时间均少于GPSR-BB，而当随机取初值时，非单调的GPSR-BB甚至求解失败，表2中“-”表示迭代次数超过迭代上限仍未能终止。

5. 结语

压缩感知利用原始信号的稀疏性，通过求解稀疏优化问题来恢复原始信号。Stephen Wright等人提出的稀疏信号重构的B-B步长的梯度投影(GPSR-BB)算法简单有效，受到广泛关注。本文在GPSR-BB算法的基础上，提出了预测校正的梯度投影法。数值结果表明新算法比GPSR-BB算法的求解效率要稍好些，且取不同初值时均可有效求解。

资助信息

海南省科协青年科技人才学术创新计划项目资助(No. HAST201622)。

文章引用

胡剑峰. 一种改进的稀疏信号重构的梯度投影算法
An Improved Gradient Projection Method for Sparse Signal Reconstruction[J]. 计算机科学与应用, 2017, 07(09): 828-833. http://dx.doi.org/10.12677/CSA.2017.79095

参考文献 (References)