Operations Research and Fuzziology
Vol.06 No.01(2016), Article ID:16987,9
pages
10.12677/ORF.2016.61004
Parameter Estimation of the Fuzzy Logistic Regressive Model with LR Typed Fuzzy Coefficients
Yi Chen, Lili Wei
School of Mathematics and Computer, Ningxia University, Yinchuan Ningxia

Received: Jan. 29th, 2016; accepted: Feb. 20th, 2016; published: Feb. 25th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The classical logistic regression model is appropriate for the problems of binary variable. Since the observations were not crisp value, response variable was often between 0 and 1 and no probability distribution can be considered for response variable; hence error can not be completely regarded as random aspect. Therefore, by combining the classical logistic regression model with fuzzy sets theory, a fuzzy logistic regression model of crisp input and fuzzy output data is constructed; the coefficients and outputs are LR type fuzzy numbers. Considering the possibilities of success instead of the probabilities, the possibilities of success are described by some linguistic terms. Then the distance between two fuzzy numbers is constructed by cut sets. The least squares estimation of fuzzy parameters is obtained in proposed model based on the distance. Finally, the capability index MSI = 0.54 showed that the proposed model is effective of an ordinary one in the modeling Lupus.
Keywords:Fuzzy Nonlinear Regression, Possibility Odds, Fuzzy Least Squares Method, Capability Index Format

系数为LR-型模糊数的模糊Logistic回归模型的参数估计
陈怡,魏立力
宁夏大学数学计算机学院,宁夏 银川

收稿日期:2016年1月29日;录用日期:2016年2月20日;发布日期:2016年2月25日

摘 要
针对二分类变量问题,经典Logistic回归是合适的。由于观测结果的不精确,响应变量往往介于0,1之间,且没有概率分布,误差也不能完全看作随机性现象。为此,将经典Logistic回归模型与模糊集理论相结合,构建了具有清晰输入–模糊输出的一类模糊Logistic回归模型,其中系数与输出均用LR-型模糊数表示。用成功的可能性替代概率,这些可能性可以由一些语义词描述。然后基于截集构造了模糊数之间的距离,利用此距离得到了上述模型中模糊参数的最小二乘估计。最后将模型应用在狼疮中并通过相容性指数MSI = 0.54说明该模型的有效性。
关键词 :模糊非线性回归,可能性优势,模糊最小二乘法,相容性指数

1. 引言
基于模糊集理论的模糊回归分析模型对于处理模糊或不精确数据的分析提供了强有力的工具。近几十年来主要发展了两类主要的模糊回归方法。第一类是1982年Tanaka [1] 提出的可能性回归,该模型具有模糊系数和离散输入变量,从而使得模糊性最小化;另一类是1987年Celmins和Diamond [2] [3] 同时提出的模糊最小二乘法。目的是使得模糊数之间的距离最小化。这些模糊回归模型都是线性模型,近年来非线性模糊回归模型成为模糊回归分析的一个研究热点。
作为最流行的非线性模型之一的经典Logistic回归的响应变量服从伯努利分布 [4] 。但实际中由于不同原因导致观测结果不精确,变化的模型误差不能完全归功于随机性现象,故将Logistic回归模型和模糊集理论相结合作为一种新的模型,即模糊Logistic回归模型。
文献 [5] 提出模糊类Logistic模型,并利用模糊分类最大似然算法估计模型中的参数;文献 [6] [7] 研究了具有清晰解释变量、模糊响应变量的模糊Logistic回归模型,提出并介绍了可能性优势;文献 [8] 在最小绝对偏差方法的基础上对具有清晰输入-模糊输出数据的模糊Logistic回归模型的参数做出估计;文献 [9] 利用Dk距离对LR-型模糊数的多元模糊线性回归模型进行了研究;文献 [10] 通过将模糊观测数据用区间来表示,然后利用区间的左、右端点和中点的数据集求出传统线性回归模型相应的回归系数;文献 [11] 应用模糊结构元理论,研究了系数为有界闭模糊数的多元线性回归模型。
本文对具有清晰输入-模糊输出的模糊Logistic回归模型的参数进行估计,其中输出与系数均是LR-型模糊数。其次由于二分观测结果的模糊性,响应变量没有概率分布。这种模糊性可以通过可能性来评估和度量,用一些语义词描述可能性,并将语义词看作LR-型模糊数。然后基于截集构造了模糊数之间的距离,利用此距离得到上述模型中模糊参数的最小二乘估计。最后将模型应用在临床案例中并通过相容性指数获得模型拟合的具体情况。
2. Logistic回归
2.1. 经典Logistic回归
经典Logistic回归模型主要研究二分类的响应变量与影响结果的一些解释变量之间的关系。在这里解释变量可以是离散型、连续型或混合型,且没有假设分布。响应变量Y={0,1}(失败/成功)通常服从伯努利分布,即 ,
, 。
。
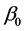 与
与 ,i³分别是回归截距和回归系数,Yij是第i个个体的第j个观测值,
,i³分别是回归截距和回归系数,Yij是第i个个体的第j个观测值, 表示x的每一个预测变量
表示x的每一个预测变量 处“成功”的概率,则拥有n个预测变量的
处“成功”的概率,则拥有n个预测变量的 的Logistic回归模型为
的Logistic回归模型为
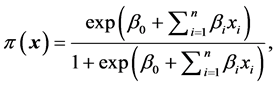
经过Logit转化得到
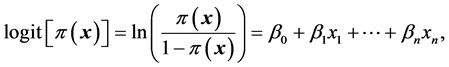
其中,表达式 称为概率优势,
称为概率优势,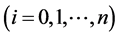
 是模型中的参数。
是模型中的参数。
当 ,并且控制x中的一部分预测变量
,并且控制x中的一部分预测变量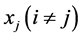 不变时,预测变量
不变时,预测变量 每增加1个单位对多元Logistic回归模型的优势影响为
每增加1个单位对多元Logistic回归模型的优势影响为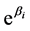 倍。
倍。
2.2. 模糊Logistic回归
在临床研究中,由于缺少合适的仪器或明确的标准,个体样本无法分类 [8] 。在实际中,更可行的措施是用语言变量来表示响应变量,这时响应类别是相对模糊的且不能认为其服从伯努利分布。这种模糊性可以通过成功的可能性来评估和度量。Pourahmad等人在文献 [7] 提出了“可能性优势”的概念:
定义2.1:设 是第i个个体成功可能性,
是第i个个体成功可能性, 。成功可能性有两种情况:1) 精确值,
。成功可能性有两种情况:1) 精确值, ,
, ;2) 语义词,
;2) 语义词, ,用合适的模糊数来定义
,用合适的模糊数来定义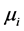 ,且
,且 支撑的并覆盖了整个(0, 1)区间。比值
支撑的并覆盖了整个(0, 1)区间。比值 是第i个个体的可能性优势。
是第i个个体的可能性优势。
文献 [7] 讨论了第一种情况。本文主要讨论第二种情况,即具有模糊二分预测结果的Logistic回归模型,成功可能性由语义词 来代替。
来代替。 通常定义为LR-型模糊数,如下
通常定义为LR-型模糊数,如下
 (1)
(1)
Pourahmad将对数 转化得到的可能性优势
转化得到的可能性优势 看作观测结果,这些观测结果的隶属函数通过扩张原理以及
看作观测结果,这些观测结果的隶属函数通过扩张原理以及 的隶属函数来确定,如下:
的隶属函数来确定,如下:
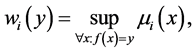
 是一对一的函数,因此
是一对一的函数,因此
 (2)
(2)
设有一组精确的解释变量以及模糊的观测结果 ,用解释变量回归对数转化后的可能性优势
,用解释变量回归对数转化后的可能性优势 ,即模糊Logistic回归模型为:
,即模糊Logistic回归模型为:
 (3)
(3)
其中 是LR-型模糊数,
是LR-型模糊数, ,
, 是正实数。
是正实数。
3. 模糊最小二乘法
模糊最小二乘法由Celmins和Diamond同时提出,是最小二乘法的模糊扩展。因此一个合适的模糊数的距离定义是必要的。
定义3.1 [12] :设E是函数空间,则对,基于函数之间的距离为:
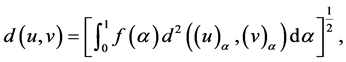
其中 ,且
,且 ,
,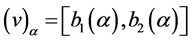 分别是u,v的
分别是u,v的 截集,函数
截集,函数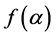 是
是 的权重因子,在区间[0,1]上单调递增,满足
的权重因子,在区间[0,1]上单调递增,满足 ,
, 。通常将
。通常将 看作是权重函数。
看作是权重函数。
为了获得最佳模型,预测变量 以及观测结果
以及观测结果 之间误差平方和(SSE)应该最小。由定义3.1得到
之间误差平方和(SSE)应该最小。由定义3.1得到
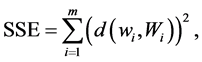
其中 。
。
为了不失一般性,我们假设 ,估计出的结果
,估计出的结果 ,
, 也是LR-型模糊数。其中
也是LR-型模糊数。其中 ,
, ,
, ,
, 。通过计算得到:
。通过计算得到:
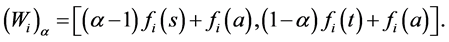
为了计算 ,设
,设 ,此时
,此时
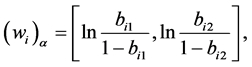
则
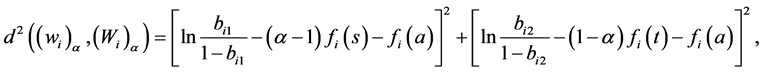
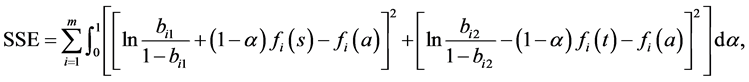
SSE仅依赖模型系数 。为求解SSE的最小值,令偏导
。为求解SSE的最小值,令偏导 ,
, ,以及
,以及 等于0,得到
等于0,得到
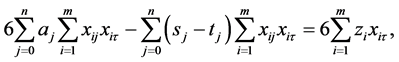
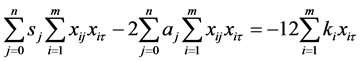 (4)
(4)
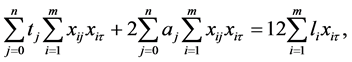
其中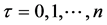
公式(4)的矩阵表示为
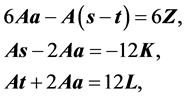
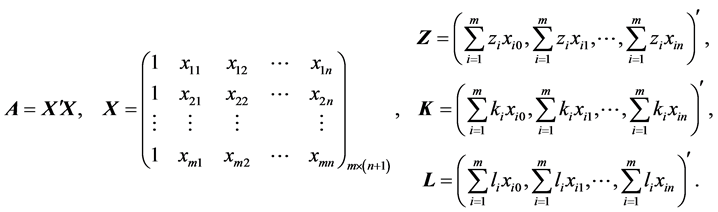
当 ,
, 存在。则SSE的最小值具有唯一解 [12] :
存在。则SSE的最小值具有唯一解 [12] :
 (5)
(5)
考虑到 ,则有
,则有
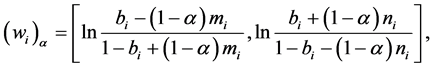
由公式(2)解得 的隶属函数为:
的隶属函数为:
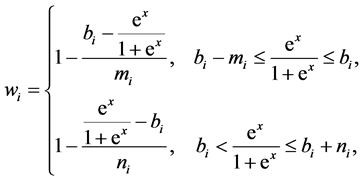
4. 拟合优度
论文利用文献 [13] 提出的相容性指数评估模型估计值与观测值的具体拟合情况。
定义4.1设A,B是两个模糊数,则A和B之间的相容性指数定义如下:
 (6)
(6)
其中∩与∪分别是两个模糊集的“最小”与“最大”运算。
定理4.1 [13] :设A,B是两个模糊数,则
1) 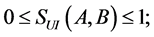
2) 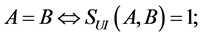
3) 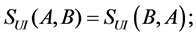
4) 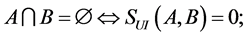
5) 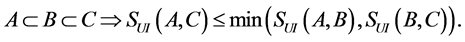
定义4.2 [14] :对于模糊Logistic回归模型,相容性指数是评估模型拟合优度的一种度量:
 (7)
(7)
显然大的MSI对应更好的拟合优度。
5. 一个临床医学的实例分析
这个数值案例来自参考文献 [7] 。系统性红斑狼疮(Systematic Lupus Erythematosus,简称SLE)是一种慢性自体免疫疾病,产生的抗体会攻击身体中的多个系统。由于这种疾病的潜伏期较长,因此对于狼疮没有良好的诊断试验。Physicians尝试从之前的病史、试验以及现有的症状中收集信息。他们制定了11个标准来诊断对象是否患有SLE [7] 。通常,在做出诊断之前一个人至少要满足上述标准中的4个。那么如果一个人满足其中3个标准,这个人是否健康?或者对满足多于3个标准的患者,他们的患病严重程度是否相同?
SLE在区分患者与正常人之间的界限并不清晰. 因此, 有研究者利用语义词对每个样本患病的可能性赋值:{非常低,低,中,高,非常高}。SLE的患病可能性的定义见公式(1)。为了研究SLE患病的可能性优势与表1提到的影响因子之间的关系,提出如下模型:
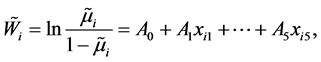
Table 1. Fuzzy binary observations in SLE disease and the values of related risk factors
表1. SLE模糊二分观测数据以及相关的影响因子
其中 ,
,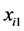 是关于疾病的家族史;
是关于疾病的家族史;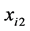 是光暴露;
是光暴露; 是ANA试验结果;
是ANA试验结果;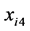 是Anti-DNA试验结果;
是Anti-DNA试验结果; 是ESR试验结果。
是ESR试验结果。
为了估计系数 ,
,
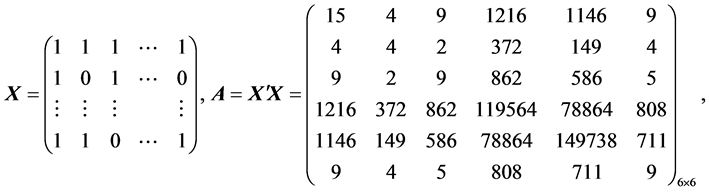
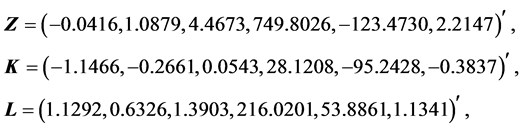
由于rank(A) = 6,公式(5)有唯一的解:
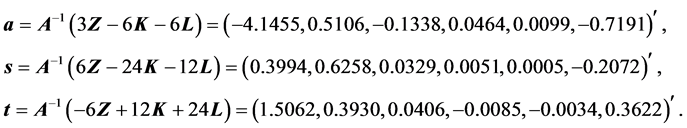
上述结果中s5,t3,t4均小于0,违反了模糊数的基本性质,但是这些数都非常接近0,故令这些数等于0,得到最终模型:
 (8)
(8)
利用公式(8)的模型可以估计人们患有狼疮的可能性。例如,对于第3个样本(0, 1, 115, 15, 0)得到的估计结果为:
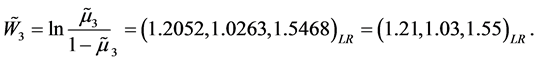
根据扩张原理得到可能性优势的隶属函数为:
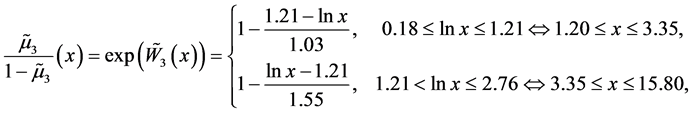
以及具有狼疮可能性的隶属函数:
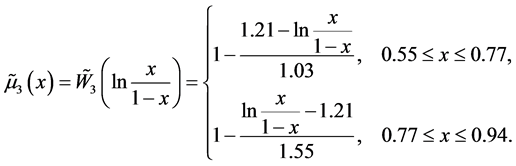
假设有一个新的样本,其信息为(0, 1, 110, 87, 0),通过得到的模型估计患病的可能性优势为:
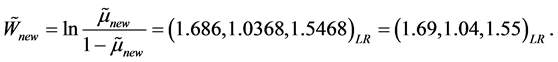
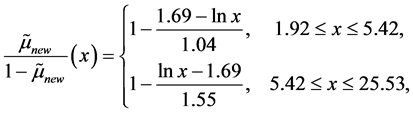
以及具有狼疮可能性的隶属函数:
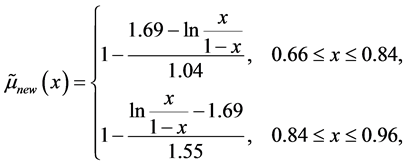
并且根据定义4.1、定义4.2得到模型的相容性指数为:
 .
.
MSI > 0.50,说明模糊Logistic回归具有很好的拟合结果。
在临床医学中,经典Logistic回归模型响应变量的取值为0 (没患病)或1 (患病),而模糊Logistic回归响应变量的取值为五个语义词:{非常低,低,中,高,非常高},这样更加符合实际情况。
6. 结论
在经典Logistic回归分析中,解释变量是没有假设分布的 [15] ,二分响应变量往往服从伯努利分布。但实际中二分响应变量的观测结果普遍模糊且没有概率分布。忽视这类观测结果是不合理的,这就需要一个新的模型。
本文利用模糊最小二乘法来估计具有清晰输入-模糊输出的模糊Logistic回归模型中的参数。成功可能性由语义词表示为:{非常低,低,中,高,非常高},这些语义词支撑的并覆盖了(0, 1)区间。本文选择第二种定义,然后将每一个样本的成功可能性进行对数转化得到 。基于两个模糊数的距离定义,利用模糊最小二乘法估计模型中的参数。同时给出评估模型的一个拟合优度准则,最后利用所提出的模型来研究一个关于狼疮的实例。
。基于两个模糊数的距离定义,利用模糊最小二乘法估计模型中的参数。同时给出评估模型的一个拟合优度准则,最后利用所提出的模型来研究一个关于狼疮的实例。
与之前的研究相比,本文的方法具有一些优点:
1) 将模糊线性回归扩展到模糊非线性回归;
2) 用可能性替代概率,语义词表示观测结果,使得模型更加完善;
3) 观测结果与系数均用LR-型模糊数表示,计算简单且在实践中更常见;
4) 基于 截集构造模糊数之间的距离相比基于模糊数的三个点(左端点、中间、右端点)更加准确;
截集构造模糊数之间的距离相比基于模糊数的三个点(左端点、中间、右端点)更加准确;
5) 利用相容性指数获得模型拟合的具体情况。
本文研究了清晰输入-模糊输出的模糊Logistic回归模型,此回归模型还可以扩展到输入输出及系数均为LR-型模糊数或其它类型模糊数,利用模糊最小二乘法来估计相应模型中的参数。
致谢
非常感谢我的导师魏立力老师对我的指导,从论文的定题, 到参考文献的查阅,到写作、修改,到最后的定稿,魏老师给了我耐心的指导和无私的帮助。魏老师的这种无私奉献的敬业精神令我钦佩,他不仅教会了我如何学习,也教会了我如何做人。在此我向魏老师表示我诚挚的谢意!
基金项目
国家自然科学基金资助项目(11261044)。创新项目:宁夏大学研究生创新项目(GIP2015034)。
文章引用
陈 怡,魏立力. 系数为LR-型模糊数的模糊Logistic回归模型的参数估计
Parameter Estimation of the Fuzzy Logistic Regressive Model with LR Typed Fuzzy Coefficients[J]. 运筹与模糊学, 2016, 06(01): 27-35. http://dx.doi.org/10.12677/ORF.2016.61004
参考文献 (References)
- 1. Tanka, H., Uejima, S. and Asai, K. (1982) Linear Regression Analysis with Fuzzy Model. IEEE Transactions on Sys-tems, Man, and Cybernetics, 12, 903-907. http://dx.doi.org/10.1109/TSMC.1982.4308925
- 2. Celmins, A. (1987) Least Squares Model Fitting to Fuzzy Vector Data. Fuzzy Sets System, 22, 245-269. http://dx.doi.org/10.1016/0165-0114(87)90070-4
- 3. Diamond, P. (1987) Least Squares Fitting of Several Fuzzy Variables. Proceedings of the second IFSA Congress, Tokyo, 20-25.
- 4. Agresti, A. (2002) Categorical Data Analysis. John Wiley & Sons, New York. http://dx.doi.org/10.1002/0471249688
- 5. Yang, M. and Chen, H. (2004) Fuzzy Class Logistic Regression Analysis. Fuzziness and Knowledge Based Systems, 12, 761-780. http://dx.doi.org/10.1142/S0218488504003193
- 6. Pourahmad, S., Ayatollahi, S.M.T. and Taheri, S.M. (2001) Fuzzy Logistic Regression: A New Possibilistic Model and Its Application in Clinical Vague Status. Iranian Journal of Fuzzy Systems, 1, 1-17.
- 7. Pourahmad, S., Ayatollahi, S.M.T., Taheri, S.M., et al. (2011) Fuzzy Logistic Regression Based on the Least Squares Approach with Application in Clinical Studies. Computers and Mathematics with Application, 62, 3353-3365. http://dx.doi.org/10.1016/j.camwa.2011.08.050
- 8. Namdari, M., Yoon, J.H., Abadi, A., et al. (2015) Fuzzy Logistic Regression with Least Absolute Deviations Estimators. Soft Computing, 19, 909-917. http://dx.doi.org/10.1007/s00500-014-1418-2
- 9. 梁艳, 魏立力. 系数为LR-型模糊数的模糊线性最小二乘回归[J]. 模糊系统与数学, 2007, 21(3): 112-117.
- 10. 张爱武. 系数为LR-型模糊数的模糊回归模型的参数估计[J]. 模糊系统与数学, 2013, 27(6): 140-147.
- 11. 岳立柱. 系数为一般模糊数的多元线性回归模型[J]. 统计与决策, 2015(3): 72-74.
- 12. Xu, R. and Li, C. (2001) Multidimensional Least Squares Fitting with a Fuzzy Model. Fuzzy Sets and Systems, 119, 215-223. http://dx.doi.org/10.1016/S0165-0114(98)00350-9
- 13. Taheri, S.M. and Kel-kinnama, M. (2012) Fuzzy Linear Regression Based on Least Absolutes Deviations. Iranian Journal of Fuzzy Systems, 9, 121-140.
- 14. Kelkinnama, M. and Taheri, S.M. (2012) Fuzzy Least Absolutes Regression Using Shape Preserving Operations. Information Sciences, 214, 10 5-120.
- 15. Domr, M., Zain, R., Kareem, S.A., et al. (2007) An Adaptive Fuzzy Regression Model for the Prediction of Dichotomous Response Variables. Computational Science and Applica-tions, 15, 14-19.
