Operations Research and Fuzziology
Vol.07 No.01(2017), Article ID:19808,6
pages
10.12677/ORF.2017.71004
A Three-Term Conjugate Gradient Algorithm for Nonlinear Equations Problems
Linghua Huang
School of Information and Statistics, Guangxi University of Finance and Economics, Nanning Guangxi

Received: Feb. 6th, 2017; accepted: Feb. 21st, 2017; published: Feb. 24th, 2017

ABSTRACT
This paper designs a three-term conjugate gradient algorithm for nonlinear equations problems and the proposed algorithm has four advantages: (1) the sufficient descent property is satisfied for the search direction; (2) the trust region feature holds for the direction too; (3) the global convergence of the proposed algorithm is possessed; (4) the new algorithm can successfully solve nonlinear equations problems with 1000 dimensions.
Keywords:Nonlinear Equations Problems, Three-Term Conjugate Gradient, Global Convergence
非线性方程组问题的一个三项共轭梯度算法
黄玲花
广西财经学院信息与统计学院,广西 南宁
收稿日期:2017年2月6日;录用日期:2017年2月21日;发布日期:2017年2月24日

摘 要
本文设计一个三项共轭梯度算法,用来求解非线性方程组问题,建议的算法优点是:(1) 搜索方向的充分下降性;(2) 搜索方向的信赖域特点;(3) 算法能保证具有全局收敛性;(4) 算法能成功求解一千维以上的非线性方程组问题。
关键词 :方程组问题,三项共轭梯度,全局收敛性

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文研究下面的非线性方程组问题:
 (1.1)
(1.1)
 是连续可微函数,不难看出问题(1.1)的求解等价于求解如下形式的最小值优化问题模型:
是连续可微函数,不难看出问题(1.1)的求解等价于求解如下形式的最小值优化问题模型:
 (1.2)
(1.2)
其中 表示欧式范数。则非线性方程组问题(1.1)就转化为了一个最小值的优化问题(1.2),我们将对(1.2)提出其求解的新算法。求解一个最优化问题,常采用数值迭代方法,一般的迭代公式定义为
表示欧式范数。则非线性方程组问题(1.1)就转化为了一个最小值的优化问题(1.2),我们将对(1.2)提出其求解的新算法。求解一个最优化问题,常采用数值迭代方法,一般的迭代公式定义为
 (1.3)
(1.3)
 是搜索方向,
是搜索方向,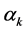 表示步长,
表示步长, 代表第
代表第 次迭代点(或称为当前点),有了
次迭代点(或称为当前点),有了 和
和 ,产生第
,产生第 个迭代点
个迭代点 (或称为下一个迭代点);依次类推,根据(1.3)产生一个迭代序列
(或称为下一个迭代点);依次类推,根据(1.3)产生一个迭代序列 ,设计算法主要是分析迭代序列
,设计算法主要是分析迭代序列 是否收敛到某一聚点
是否收敛到某一聚点 或得到
或得到 ?
?
本文将针对(1.2)设计一个新的三项共轭梯度法,众所周知共轭梯度算法是一类非常有效的求解目标函数最小值的优化方法 [1] [2] [3] [4] [5] ,特别是对大规模优化问题,其搜索方向定义形式是:

 表示共轭梯度参数,它是共轭梯度法设计的关键。鉴于此方法设计简单、程序容易实现,很多学者便成功将此类方法应用于(1.1)的求解(见文献 [6] [7] [8] 等),受此启发,我们将做进一步的研究,设计一个三项共轭梯度算法,新方法具有不错的性质和特点。第二部分,给出设计好的三项共轭梯度方法和及其具体的算法步骤,第三部分分析算法的下降性、信赖域特点和全局收敛性,第四部分进行非线性方程组问题的检验。
表示共轭梯度参数,它是共轭梯度法设计的关键。鉴于此方法设计简单、程序容易实现,很多学者便成功将此类方法应用于(1.1)的求解(见文献 [6] [7] [8] 等),受此启发,我们将做进一步的研究,设计一个三项共轭梯度算法,新方法具有不错的性质和特点。第二部分,给出设计好的三项共轭梯度方法和及其具体的算法步骤,第三部分分析算法的下降性、信赖域特点和全局收敛性,第四部分进行非线性方程组问题的检验。
2. 公式和算法
建议的三项共轭梯度公式如下:
 (2.1)
(2.1)
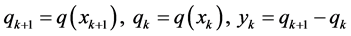 ,
,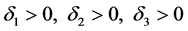 是常数。上述公式的思想是受文章 [7] [8] 启发设计的。下面给出该三项共轭梯度算法详细步骤:
是常数。上述公式的思想是受文章 [7] [8] 启发设计的。下面给出该三项共轭梯度算法详细步骤:
算法1:(三项共轭梯度算法)
步骤0:初始条件的赋值,初始迭代点 ,常数
,常数 ,置
,置 。
。
步骤1:条件 满足,停止算法;否则转步骤2。
满足,停止算法;否则转步骤2。
步骤2:解(2.1)获得搜索方向 。
。
步骤3:通过下面线搜索技术
 (2.2)
(2.2)
获得步长 。
。
步骤4:置 。
。
步骤5:如果条件 满足,算法停止并取
满足,算法停止并取 ;否则置
;否则置
 (2.3)
(2.3)
步骤6:置 ,转到步骤1。
,转到步骤1。
注:线搜索技术(2.2)是文献 [7] 最先给出,(2.3)是投影技术,由文献 [9] 给出。
3. 信赖域特点、充分下降性以及全局收敛性
我们首先通过下面的引理证明算法1的信赖域的特点和充分下降性。
引理3.1:(2.1)产生的搜索方向 满足
满足
 (3.1)
(3.1)
和
 (3.2)
(3.2)
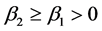 是常数。
是常数。
证明:根据(2.1)的定义形式, 时,不难获得(3.1)和(3.2)。下面讨论
时,不难获得(3.1)和(3.2)。下面讨论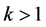 时的情况,同样利用(2.1)有
时的情况,同样利用(2.1)有

从而获得(3.1)。根据(3.1)的结果,易得

取 ,则(3.2)式的左边成立。关于(3.2)的右边不等式,需要再次利用(2.1)来获得,具体如下
,则(3.2)式的左边成立。关于(3.2)的右边不等式,需要再次利用(2.1)来获得,具体如下

最后一个不等式利用了 获得,任取
获得,任取 ,(3.2)的右边不等式便能获得。综上所述,关系式(3.1)和(3.2)都是成立的。证毕!
,(3.2)的右边不等式便能获得。综上所述,关系式(3.1)和(3.2)都是成立的。证毕!
关系式(3.1)被称为充分下降性,而关系式(3.2)被称为信赖域的特征。从证明过程可以看出,我们建议的三项共轭梯度的搜索方向在没有其他假设条件的情况下,自身就能拥有这两个优点,关系式(3.1)和(3.2)对算法的收敛性起着至关重要的作用。为进一步获得三项共轭梯度算法的全局收敛性,需要一些假设条件。
假设A:(i) 假设问题(1.1)的解存在;
(ii) 满足Lipschitz条件,也就是
满足Lipschitz条件,也就是
 ,
,
 是Lipschitz常数。
是Lipschitz常数。
根据假设A和获得的引理3.1,便可以证明算法1的全局收敛性结论。此结论的证明与参考文献 [7] 的证明过程相似,我们就不再详述。
定理3.1:若迭代序列 是由算法1产生的且假设A的条件满足,则关系式
是由算法1产生的且假设A的条件满足,则关系式

成立。
此定理被称为算法1的全局收敛性定理。
4. 数值实验
为验证建议的三项共轭梯度算法是有效的,本节将对下面的问题(见表1)利用计算机编写程序计算。
我们将利用Matlab R2009a编写程序代码,程序是在Windows 7系统、CPU为Intel (R) Xeon (R),E5507 2.27 GHz、64位操作系统、6.00GB内存上运行。算法中的参数选取分别是: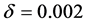 ,
, ,
, ,
,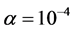 。表2中第一行参数含义分别是:NI代表迭代次数,Nq代表函数值次数,Dim代表所检验问题的维数,Cpu-Time代表程序在计算机上运行的CPU时间,Val代表程序终止时的范数值。
。表2中第一行参数含义分别是:NI代表迭代次数,Nq代表函数值次数,Dim代表所检验问题的维数,Cpu-Time代表程序在计算机上运行的CPU时间,Val代表程序终止时的范数值。
Table 1. Problems name
表1. 问题名称
Table 2. Numerical results
表2. 数值结果
从表格中测验结果能够看出:(1) 给定的三项共轭梯度算法能成功求解这10个非线性方程组问题,范数值接近于零说明利用新算法几乎得到了其精确解,其中第十个问题就获得了精确解;(2) 随着检验问题规模的增大,NI和Nq的变化不大,有的个别问题反而减少,但Cpu-Time均会适当增加,这也证明了算法的合理性;(3) 有些问题的Cpu-Time = 0,这证明算法在运行时,几乎没有占用系统的CPU时间。
文章引用
黄玲花. 非线性方程组问题的一个三项共轭梯度算法
A Three-Term Conjugate Gradient Algorithm for Nonlinear Equations Problems[J]. 运筹与模糊学, 2017, 07(01): 31-36. http://dx.doi.org/10.12677/ORF.2017.71004
参考文献 (References)
- 1. Andrei, N. (2008) Another Hybrid Conjugate Gradient Algorithm for Unconstrained Optimization. Numerical Algorithms, 47, 143-156. https://doi.org/10.1007/s11075-007-9152-9
- 2. Fletcher, R., Reeves, C.M., et al. (1964) Function Minimization by Conjugate Gradients. Computer Journal, 7, 149-154. https://doi.org/10.1093/comjnl/7.2.149
- 3. Polak, E. and Ribière, G. (1968) Note sur la convergence de méthodes de directions conjuguées. Rev. Francaise Imformat Recherche Opertionelle, 16, 35-43.
- 4. Wei, Z., Yao, S. and Liu, L. (2006) The Convergence Properties of Some New Conjugate Gradient Methods. Applied Mathematics & Computation, 183, 1341-1350. https://doi.org/10.1016/j.amc.2006.05.150
- 5. Yuan, G. (2009) Modified Nonlinear Conjugate Gradient Methods with Sufficient Descent Property for Large-Scale Optimization Problems. Optimization Letters, 3, 11-21. https://doi.org/10.1007/s11590-008-0086-5
- 6. Li, Q. and Li, D.H. (2011) A Class of Derivative-Free Methods for Large-Scale Nonlinear Monotone Equations. IMA Journal of Numerical Analysis, 31, 1625-1635. https://doi.org/10.1093/imanum/drq015
- 7. Li, D. and Wang, L. (2011) A Modified Fletcher-Reeves-Type Derivative-Free Method for Symmetric Nonlinear Equations. Numerical Algebra, Control and Optimization, 1, 71-82. https://doi.org/10.3934/naco.2011.1.71
- 8. Yuan, G. and Zhang, M. (2015) A Three-Terms Polak-Ribière-Polyak Conjugate Gradient Algorithm for Large-Scale Nonlinear Equations. Journal of Computational & Applied Mathematics, 286, 186-195. https://doi.org/10.1016/j.cam.2015.03.014
- 9. Solodov, M.V. and Svaiter, B.F. (1998) A Globally Convergent Inexact Newton Method for Systems of Monotone Equations. Reformulation: Nonsmooth, Piecewise Smooth, Semismooth and Smoothing Methods, Springer, US, 1411- 1414.
