Operations Research and Fuzziology
Vol.08 No.01(2018), Article ID:23828,9
pages
10.12677/ORF.2018.81004
Fuzzy Regression Combination Model and Its Application in CPI Forecasting
Lili Wei, He Li
School of Mathematics and Statistics, Ningxia University, Yinchuan Ningxia

Received: Feb. 6th, 2018; accepted: Feb. 19th, 2018; published: Feb. 26th, 2018

ABSTRACT
A fuzzy regression combination forecasting method is proposed and applied to the CPI forecasting in this paper. The method can synthesize the advantages of fuzzy regression and combination forecasting, and give a practical predicted interval value of CPI. Firstly, the quadratic curve model and the time series model be selected as the single prediction model, and the prediction results are fuzzified. Secondly, the fuzzy regression combination model is established by minimizing the fuzzy degree for the given goodness-of-fit to solve the optimal weight coefficient. Finally, the CPI forecasting results show that the fuzzy regression model is better than the single prediction model, which can improve the prediction accuracy of CPI and is suitable for short-term prediction of CPI.
Keywords:Fuzzy Regression, Combination Forecasting, CPI
模糊回归组合模型在CPI预测中的应用
魏立力,李贺
宁夏大学数学统计学院,宁夏 银川
收稿日期:2018年2月6日;录用日期:2018年2月19日;发布日期:2018年2月26日

摘 要
本文提出了一种模糊回归组合预测方法,并运用到我国CPI的预测中。该方法能综合模糊回归和组合预测的优点,给出更符合实际的CPI预测区间值。首先,选取二次曲线模型和时间序列模型作为单项预测模型,并将得到的预测结果模糊化。其次,在给定拟合度的条件下,通过极小化模糊度来建立模糊回归组合模型,求解最优权重系数。最后,CPI预测结果表明,模糊回归组合模型的预测结果优于各单项预测模型,能提高CPI的预测精度,适合对CPI进行短期预测。
关键词 :模糊回归,组合预测,CPI

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
通常由于输入或输出数据的不精确造成了经典回归模型的局限性,模糊回归模型利用模糊集理论在刻画不精确性的优势,有效的解决了这一问题。陈世全、郭嗣宗 [1] 系统地介绍了模糊预测的方法。文献 [2] 首次提出模糊回归模型,并取得较好的结果。吴冲等 [3] 提出了模糊回归预测模型。丁世飞等 [4] 也给出了一些模糊回归预测模型及应用。
在预测问题中,单纯地使用一种模型难以全面地揭示其变化规律,造成一些有用信息的丢失,给预测结果造成误差。Bates和Granger [5] 首次提出的组合预测理论能有效利用单一模型的有用信息,在提高预测准确度的同时,又能比较合理地描述客观现实。吴祈宗、宋颖 [6] 结合模糊集理论提出了一种模糊组合预测方法。
CPI是进行国民经济核算的重要指标。一般来说,国家宏观经济调控政策的出台力度受CPI的直接影响。对CPI进行定量预测研究,有利于我们认清当下经济发展的趋势,以及在制定经济政策时可以提供可靠的依据和建议。本文提出了一种模糊回归组合模型,对我国近年CPI数据进行短期的预测研究。该方法能综合模糊回归和组合预测的优点,给出更符合实际的CPI预测区间值。首先,分别选取二次曲线模型和时间序列模型作为单项预测模型对CPI进行预测,并将单项预测结果进行模糊化。其次,在给定拟合度的条件下,通过极小化模糊度来建立模糊回归组合模型。最后,应用计算机软件求得最优权重系数。
2. 模糊回归理论
2.1. 模糊集与模糊数
模糊集理论最初由Zadeh提出 [7] ,该理论将经典集推广到模糊集。这里首先介绍一些相关概念 [8] 。
定义1.1称论域X上的一个映射 为X上的一个模糊子集, 是x对A的隶属度;称 为A的 截集;称 为A的核;称 为A的支撑。记X上的全体模糊集为 。
当用模糊集来刻画模糊性时,通常需要一个度量整体模糊程度的量——模糊度。下面是模糊度的公理化定义 [8] 。
定义1.2若映射 ,满足条件:
1) 当且仅当 为经典集合时, ;
2) ,当且仅当 时, ;
3) ,当 时, ;
4) , 。
则称映射d为 上的一个模糊度。
从定义可见隶属函数值为0.5是最模糊的,这种情况下最难决策。易证,如下公式是一个模糊度。
,
其中 表示为 时A的截集。
两个模糊集间的切近度,可以表示其拟合程度。设 ,则 的拟合度为
。
如果模糊子集A满足支撑有界、核非空、截集为列紧区间,则称A为模糊数,将实数域 上的全体模糊数记为 ,模糊数是特殊的模糊集。
三角形模糊数是最常见的模糊数,因为其独特的性质而被广泛应用。设 ,如果A的隶属函数为
称A为三角模糊数。特别地,当 时,A的隶属函数为
此时,称A为对称三角形模糊数,记 , 表示中心, 表示左右扩展。
关于对称三角形模糊数有以下性质。
性质1设 ,且 ,有
1) ; 2) 。
性质2设 ,且 ,则 。
性质3设 ,且 ,则 。
2.2. 模糊线性回归模型
通常由于输入或者输出数据的不精确造成了经典回归模型的局限性,模糊回归模型利用模糊集理论在刻画不精确性的优势,可以有效地解决这一问题。模糊回归模型通过得到变量间有用的信息,从而能对研究的问题做出更好的预测。因此,模糊回归在预测方面有着广泛的应用前景。
模糊线性回归模型
, (1)
其中, 是模糊回归系数,隶属函数为
是模糊回归系数的精确值, 和 分别是模糊回归系数的中心和扩展。
设有样本观察值 。由模糊理论可知模型(1)的输出是对称三角形模糊数
。
模糊回归的目的是求解模糊回归系数 ,即求解 的中心 和扩展 。在模糊回归求解时还需满足以下条件:
1) 对于给定参数 ,使得 。
2) 由于对称三角形模糊数的模糊度与扩展 有关。因而定义模型(1)的糊度为
。
因此,对模型(1)参数的求解等价于找到最小参数A,使得在给定 的条件下 最小,即
(2)
3. 模糊回归组合预测
在对某一问题进行预测研究时,单纯地使用一种模型难以全面地揭示其变化规律,造成一些有用信息的丢失,给预测结果造成误差。Bates和Granger提出的组合预测模型能高效利用单一模型信息,减少随机因素影响。在提高预测准确度的同时,又能够比较合理地描述客观现实。
用 种单一模型对同一对象做预测,可构建的组合预测模型为
, (3)
其中, 为第t期的组合预测值, ; 为第i种方法在t时的预测值, ; 为第i种方法的权系数, 。 为t期的组合预测误差,其中, 为第i种方法在t期的预测误差, 为第t期的实际观测值。
组合预测的目的是在观测值与预测值拟合度最大的条件下求解最优权重系数。本文将单项预测值模糊化,来代替模糊线性回归中的 ,并在给定拟合度的条件下,通过极小化模糊度建立模糊回归组合模型来求解最优的权重系数,模型具体的构建步骤如下。
将 期的实际观测值 模糊化描述为 , 为给定的置信值。将 期第 种单项模型的预测值 模糊化描述为 , ,其中 是置信值,取值与 和置信水平有关,
。
模糊化后的组合预测模型表示为
。 (4)
的隶属函数表示为
与 的拟合度表示为
。
模型(4)的模糊度为
。
为此,我们建立的模糊回归组合模型为
(5)
其中,H为给定的拟合度。为了方便求解模型,引入新的变量为:
因此,模型(5)可以转化为:
(6)
4. CPI实例应用
本章用模糊回归组合模型对全国月度同比数据进行预测验证。图1给出了全国CPI月度同比数据变化趋势图。
1) 二次曲线预测模型
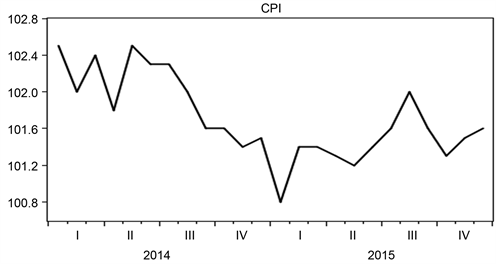
Figure 1. CPI trends
图1. CPI的变化趋势
拟合图1中CPI变化趋势,选用二次曲线预测模型。利用Eviews对模型进行参数求解。可以看出,参数 值都很小,结果显著,说明模型效果良好。模型 为
(7)
2) 时间序列模型
在以往的时间序列分析中,用模型 对 进行长期趋势预测时,由于误差 存在序列相关,不能满足对 的经典假设,所以要对传统的时间序列模型进行改进修正。改进后的模型先对 的长期趋势利用上述模型进行拟合,然后对实际观测值减去趋势值后的误差 进行差分,建立ARMA模型。这样既描述了 的长期变动趋势,又考虑了短期波动情况,改进后的模型为
其中, 。 为滞后算子, 是白噪声误差项。
首先,在剔除 长期随机影响后,对 建立ARMA模型。可以发现一阶差分后的 序列平稳。
其次,对 建立 模型,并进行参数估计。
最后,对 进行白噪声检验, 统计量的p值都远大于0.05,可认为是白噪声序列,说明模型信息提取比较充分。
时间序列模型 为
(8)
表1分别给出了单项模型的预测结果及误差。
将二次曲线模型 与时间序列模型 进行模糊组合,在模型(6)中,取拟合度 。将观测值与各单项预测值进行模糊化得: , , ,用Lingo对模型(6)进行求解,可得最优权重系数: 。
由表2可知,二次曲线预测模型7)的模糊度 ,时间序列模型(8)的模糊度 ,模糊回归组合模型的模糊度 。由结果可知,模糊回归组合模型的模糊度最小。同样地,预测
Table 1. Prediction results and errors of individual models
表1. 各单项模型的预测结果与误差
Table 2. Prediction results of Fuzzy regression
表2. 模糊回归预测结果
结果精确化以后,模糊回归组合模型的误差平方和为1.615,小于各单项模型的误差平方和。由此可以说明,模糊回归组合模型在CPI的预测问题上能够提高模型精度,也验证了该模型的可行性。
基金项目
国家自然科学基金项目(11261044)。
文章引用
魏立力,李 贺. 模糊回归组合模型在CPI预测中的应用
Fuzzy Regression Combination Model and Its Application in CPI Forecasting[J]. 运筹与模糊学, 2018, 08(01): 30-38. http://dx.doi.org/10.12677/ORF.2018.81004
参考文献 (References)
- 1. 陈世全, 郭嗣宗. 模糊预测[M]. 贵阳: 贵阳科技出版社, 1994.
- 2. Tanaka, H., Uejima, S. and Asai, K. (1982) Linear Regression Analysis with Fuzzy Model. IEEE Transactions on Systems, Man and Cybernetics, 12, 903-907. https://doi.org/10.1109/TSMC.1982.4308925
- 3. 吴冲, 潘启树, 李汉玲. 模糊线性回归预测[J]. 西安交通大学学报, 2000, 34(9): 100-102.
- 4. 丁世飞, 陈述汉, 苏本堂. 多元模糊回归预测模型及应用[J]. 模糊系统与数学, 2000, 14(3): 94-98.
- 5. Bates, J.M. and Granger, C.W.J. (1969) The Combination of Forecasts. Operational Research Society, 20, 451-468. https://doi.org/10.1057/jors.1969.103
- 6. 吴祈宗, 宋颖. 一种模糊组合预测方法[J]. 北京理工大学学报, 2004, 24(4): 373-376.
- 7. Zadeh, L.A. (1965) Fuzzy Sets. Information and Control, 8, 338-353. https://doi.org/10.1016/S0019-9958(65)90241-X
- 8. 杨纶标, 高英仪. 模糊数学原理及应用[M]. 第五版. 广州: 华南理工大学出版社, 2011.
