Operations Research and Fuzziology
Vol.08 No.02(2018), Article ID:25165,10
pages
10.12677/ORF.2018.82008
Pricing Decisions in a Dual Channel Supply Chain with Different Market Power Structures
Jiajing Dong, Jing Zhao*, Yunlian Guo
School of Science, Tianjin Polytechnic University, Tianjin

Received: May 8th, 2018; accepted: May 19th, 2018; published: May 29th, 2018

ABSTRACT
This paper investigates the pricing decision problem of a dual-channel supply chain consisting of one manufacturer and one retailer which opens an online channel. From the perspective of consumer utility, and considering the difference of market power among members of supply chain and the difference of relative channel power, three pricing game models are established, and the corresponding analytic equilibriums are obtained. Furthermore, we analyze the influence of the market power structure, channel substitutability and the relative channel power on the pricing strategies, the maximal demands and the maximal profits.
Keywords:Dual-Channel Supply Chain, Channel Power, Pricing Decision, Consumer Utility
不同市场权力结构下零售商双渠道供应链中 定价决策研究
董嘉婧,赵 静*,郭云莲
天津工业大学理学院,天津

收稿日期:2018年5月8日;录用日期:2018年5月19日;发布日期:2018年5月29日

摘 要
本文研究由一个制造商和一个开辟网络直销渠道的零售商组成的双渠道供应链的定价决策问题。从消费者效用角度且考虑供应链成员间市场权力的不同及两渠道相对权力的不同,建立三个博弈模型,并得到相应的解析均衡解,进而分析市场权力结构、渠道替代率及相对渠道权力对产品定价策略、最大渠道需求及最大利润的影响。
关键词 :双渠道供应链,渠道权力,定价决策,消费者效用

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
电子商务近年来迅速发展,2017中国电商年度报告显示,中国电商约占全球市场份额的40%;2016年,中国网购规模达7500亿美元。许多传统零售商如沃尔玛、乐购、苏宁等也建立网络直销渠道,形成双渠道零售商。此外,部分大型电子零售商如亚马逊、Warby Parker、京东等也建立自己的实体店,成为双渠道零售商。目前由零售商开辟网络直销渠道的双渠道供应链大量存在,而此类供应链管理的相关研究还比较少见。
已有文献对零售商双渠道供应链的研究主要关注渠道选择问题,如Hsiao和Chen [1] 探讨制造商和零售商引入网络渠道的原因和时间,并研究市场均衡问题。Wang [2] 等探讨由一个零售商和销售两种差异产品的制造商组成的供应链中制造商和零售商的双渠道选择和定价问题。King [3] 等研究电子商务对零售商双渠道策略选择的影响。Liu和Qian [4] 从品牌战略的角度,帮助零售商在网络和传统零售渠道中选择最佳的品牌战略和市场结构。Bernsteina和Zheng [5] 研究零售商之间的竞争、网络渠道的价格竞争,网络渠道对整个供应链的影响,并分析渠道结构的选择与均衡。不同于已有研究,本文在零售商开辟双渠道供应链的背景下,考虑不同市场权力下产品定价策略问题。
由于供应链企业规模大小及讨价还价能力的不同,导致供应链市场权力结构不同,从而使得供应链成员的最优策略也有所不同。目前对供应链市场权力的研究大多针对“一对一”和“多对一”供应链,如Shi等 [6] 针对由单个制造商和零售商组成的供应链,建立三种权力结构模型,研究权力结构对成员绩效的影响。Wu等 [7] 考虑一个由经销商和第三方物流服务提供商组成的供应链,研究不同权力结构对均衡解和契约设计的影响。Chen和Wang [8] 研究由手机制造商和电信运营商组成的智能手机供应链,基于不同权力结构,给出不同渠道下零售商的定价策略和运营商的补贴政策。Wei等 [9] 针对两个销售互补产品的制造商和一个零售商组成的供应链,研究不同市场权力结构对渠道成员定价及利润的影响。Luo等 [10] 研究具有品牌差异的替代产品供应链中不同市场权力对价格决策的影响。与以上文献不同,本文考虑不同市场权力结构对零售商双渠道供应链中成员定价策略和利润的影响。
消费者偏好反映消费者对不同产品和服务的喜好程度的个性化偏好,影响市场需求,一些文献用效用函数描述消费者偏好,最大化效用函数求得需求函数,如Cai [11] 由效用函数获得需求函数,研究两个单渠道和两个双渠道的供应链结构中,渠道权力结构和渠道协调对供应商、零售商和整个供应链的影响。Cai等 [12] 用效用函数获得需求函数,研究两个生产单产品的制造商和两个零售商的供应链中,收入分享对供应商和零售商的联合影响。Zhang等 [13] 考虑一个由两个制造商和两个零售商组成的供应链中,每个制造商只通过特定零售商销售产品,两个产品有相似的功能和较高的可替代性,通过效用函数获得顾客对每个渠道的需求函数,分析不同渠道替代率对价格和利润的影响。与上述研究不同,本文基于零售商双渠道的供应链,通过考虑消费者效用函数最大化获取需求函数,得到不同市场权力下产品最优定价、最大需求、最大利润,并比较渠道权力对称情况下的消费者效用。
2. 问题描述及假设
考虑一个制造商和一个零售商的供应链。制造商生产产品,以单位批发价w批发给零售商,零售商可以通过网络直销渠道(记为渠道1)以价格 将产品销售给顾客,也可以通过传统零售渠道(记为渠道2)以价格
将产品销售给顾客。
为渠道i的运营成本,
。不失一般性,本文把产品制造成本标准化为零。
将产品销售给顾客,也可以通过传统零售渠道(记为渠道2)以价格
将产品销售给顾客。
为渠道i的运营成本,
。不失一般性,本文把产品制造成本标准化为零。
产品效用函数参考Cai [11] 建立如下:
(1)
其中 为渠道i的市场基础, 为渠道i的市场需求, 是渠道替代率。当 时,两个渠道是相互独立的, 时,两渠道完全替代。
最大化(1)式,得到渠道1和2的需求如下:
(2)
(3)
定义 为渠道1对渠道2的相对渠道权力。 表示渠道1的权力大于渠道2,反之亦然。 表示两渠道权力是对称的。
制造商和零售商的利润函数如下:
(4)
(5)
3. 模型建立及求解
3.1. 制造商主导的Stackelberg (MS)博弈模型
考虑制造商拥有较大市场权力,是Stackelberg博弈领导者,零售商是跟随者。制造商首先决策批发价w,然后零售商决策直销价 和零售价 ,均使各自的利润达到最大。该MS博弈模型建立如下:
(6)
用逆向归纳法求解,得命题1。
命题1在MS模型中,最优批发价 、最优直销价 和最优零售价 如下:
(7)
(8)
(9)
命题1及以下命题的证明见附录。
3.2. 零售商主导的Stackelberg (RS)博弈模型
考虑零售商拥有较大市场权力,是Stackelberg博弈领导者,制造商是跟随者。零售商首先决策直销价 和零售价 ,随后制造商决策批发价w,RS模型如下:
(10)
用逆向归纳法求解,得命题2。
命题2在RS模型中,最优批发价 、最优直销价 和最优零售价 如下:
(11)
(12)
(13)
3.3. 纳什博弈(NG)模型
考虑制造商和零售商市场权力相当,进行Nash博弈。该模型如下:
(14)
命题3在NG模型中,最优批发价 、最优直销价 和最优零售价 如下:
(15)
(16)
(17)
4. 模型分析与管理启示
4.1. 不同博弈模型下均衡解比较
本小节对不同博弈模型下的最优定价、最大需求和最大利润进行比较分析,如表1所示。其中
, , , 。
Table 1. Maximum demand and profit under different game models
表1. 不同博弈模型下的最大需求和利润
结论1: , , 。
结论1表明,最优直销价格和最优零售价格在两个Stackelberg博弈下相同,在NG下中最低;最优批发价格在MS博弈下最高,在RS博弈下最低,此结论与Shi等 [6] 中结论一致。
结论2: , , 。
结论2表明,渠道1、渠道2的最大需求和总的最大需求在两种Stackelberg博弈下相同,在NG博弈下最大。
结论3: , , 。
结论3表明,制造商(或零售商)的最大利润在其领导下的Stackelberg博弈下最高,其次是NG模型,此结论与Shi等 [6] 中结论一致;整个供应链的最大利润在NG博弈下最高此模型对整个供应链成员最有利。
比较不同博弈模型下最大消费者效用。由于解析形式的复杂性,我们只给出渠道权力相等即 时的结果,此时 , , ,其中 、 和 分别表示MS、RS和NG模型中消费者的最大效用。
结论4: 。
结论4表明渠道权力相同时,NG博弈下消费者效用最大。
4.2. 渠道替代率对最大需求、最大利润和消费者效用的影响
结论5:
1) , ; ,其中 。
2) ,其中 ;
,其中 。
3) , 。
结论5给出了渠道替代率对最大需求的影响,结合图1、图2,可得:
1) 随着渠道替代率的增大,两个渠道的最大需求均增大。具体来说,在区域
中,
, ;在区域
中,
,
。
;在区域
中,
,
。
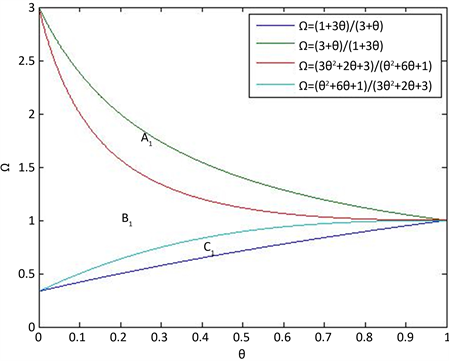
Figure 1. Maximum demand for channels change with θ (Stackelberg game)
图1. 渠道最大需求随θ改变的变化区域图(Stackelberg博弈情形)

Figure 2. Maximum demand for channels change with θ (Nash game)
图2. 渠道最大需求随θ改变的变化区域图(Nash博弈情形)
2) 随着渠道替代率的增大,直销渠道的最大需求减小,零售渠道的最大需求增大。在区域 中, , ;在区域 中, , 。
3) 随着渠道替代率的增大,渠道的最大需求减小。在区域 中, , ;在区域 中, , 。
总之,三种博弈情形下,两个渠道的最大需求和供应链总需求随渠道替代率变化趋势相同。另外,在大部分可行区域内,渠道替代率θ一定时,相对渠道权力越大,越有利于最大需求随渠道替代率增大的正增长。
结论6: , , 。
由结论6看出,渠道替代率对Stackelberg博弈领导者的最大利润影响最小,对Stackelberg博弈跟随者的最大利润影响最大,对整个供应链最大利润的影响在NG模型中较小,Stackelberg博弈模型中相同。
结论7:当渠道参数是对称的(即 , ): 。
结论7给出了在市场基础和运营成本相同时,渠道替代率对消费者效用的影响在NG博弈模型中比Stackelberg博弈模型中的影响小。
5. 结论与展望
本文研究由一个制造商和一个开辟网络直销渠道的零售商组成的供应链在不同权力结构下价格决策问题。考虑消费者效用,建立三种博弈定价模型并对最优定价策略、最大需求、最大利润进行比较分析。结果显示:最大直销价格和最大零售价格在两个Stackelberg模型中相同且高于NG博弈模型;制造商主导的Stackelberg博弈模型中最大批发价最高。两渠道和供应链总体最大需求在两种Stackelberg博弈模型中相同且低于NG博弈模型。制造商(或零售商)的最大利润在其主导下的Stackelberg博弈模型中最高,作为跟随者时最低;供应链最大总利润在NG博弈模型中最高,在Stackelberg博弈模型中最低。消费者的最大效用在纳什博弈中最大且在两个Stackelberg模型中具有相同值。在三种博弈情形下,两渠道的最大需求和总需求随渠道可替代率变化的趋势大体相同。渠道替代率对Stackelberg博弈领导者的最大利润影响最小,对Stackelberg博弈跟随者的最大利润影响最大,对整个供应链最大利润的影响在NG模型中较小,Stackelberg博弈模型中相同。在市场基础和运营成本相同时,渠道的替代率对纳什博弈中消费者效用的影响比Stackelberg博弈中的影响小。
关于不同权力结构下双渠道供应链的定价决策问题,还有待深入研究。例如,本文只研究单个制造商与零单个售商的供应链结构,未来可以研究多个制造商或多个零售商竞争的供应链结构。
基金项目
此项工作得到国家自然科学基金(71301116, 71371186)的资助。
文章引用
董嘉婧,赵 静,郭云莲. 不同市场权力结构下零售商双渠道供应链中定价决策研究
Pricing Decisions in a Dual Channel Supply Chain with Different Market Power Structures[J]. 运筹与模糊学, 2018, 08(02): 62-71. https://doi.org/10.12677/ORF.2018.82008
参考文献
- 1. Hsiao, L. and Chen, Y. (2014) Strategic Motive for Introducing Internet Channels in a Supply Chain. Production & Operations Management, 23, 36-47. https://doi.org/10.1111/poms.12051
- 2. Wang, W., Li, G. and Cheng, T.C.E. (2016) Channel Selection in a Supply Chain with a Multi-Channel Retailer: The Role of Channel Operating Costs. International Journal of Production Economics, 173, 54-65. https://doi.org/10.1016/j.ijpe.2015.12.004
- 3. King, R.C., Sen, R. and Xia, M. (2004) Impact of Web-Based E-Commerce on Channel Strategy in Retailing. International Journal of Electronic Commerce, 8, 103-130.
- 4. Liu, X.F. and Qian, X.D. (2017) Product Brand Differentiation and Dual-Channel Store Performances of a Multi-Channel Retailer. Education Teaching Forum, 44, 672-692.
- 5. Bernsteina, F. and Zheng, X. (2008) “Bricks-and-Mortar” vs. “Clicks-and-Mortar”: An Equilibrium Analysis. European Journal of Operational Research, 187, 671-690. https://doi.org/10.1016/j.ejor.2006.04.047
- 6. Shi, R., Zhang, J. and Ru, J. (2015) Impacts of Power Structure on Supply Chains with Uncertain Demand. Production &Operations Management, 20 Contracts for Fresh Product Outsourcing Logistics Channels with Power Structures. International Journal of Production Economics, 160, 94-105. https://doi.org/10.1016/j.ijpe.2014.10.007
- 7. Wu, Q., Mu, Y. and Feng, Y. (2015) Coordinating Channel Selection Decisions under Different Power Structures. Omega, 53, 11-20.
- 8. Chen, X. and Wang, X. (2015) Free or Bundled: Channel Selection Decisions under Different Power Structures. Omega, 53, 11-20. https://doi.org/10.1016/j.omega.2014.11.008
- 9. Wei, J., Zhao, J. and Li, Y. (2013) Pricing Decisions for Complementary Products with Firms’ Different Market Powers. European Journal of Operational Research, 224, 507-519. https://doi.org/10.1016/j.ejor.2012.09.011
- 10. Luo, Z., Chen, X., Chen, J., et al. (2016) Optimal Pricing Policies for Differentiated Brands under Different Supply Chain Power Structures. European Journal of Operational Research, 259, 437-451. https://doi.org/10.1016/j.ejor.2016.10.046
- 11. Cai, G. (2010) Channel Selection and Coordination in Dual-Channel Supply Chains. Journal of Retailing, 86, 22-36. https://doi.org/10.1016/j.jretai.2009.11.002
- 12. Cai, G., Dai, Y. and Zhou, S.X. (2012) Exclusive Channels and Revenue Sharing in a Complementary Goods Market. Marketing Science, 31, 172-187. https://doi.org/10.1287/mksc.1110.0688
- 13. Zhang, R., Liu, B., Wang, W., et al. (2012) Pricing Decisions in a Dual Channels System with Different Power Structures. Economic Modelling, 29, 523-533. https://doi.org/10.1016/j.econmod.2011.08.024
附录
命题1的证明: 分别对 和 求一阶偏导数得:
(a1)
 (a2)
(a2)
由(a1)和(a2)易得Hessian矩阵:
(a3)
因 ,Hessian矩阵负定,因此式(5)是 、 的凹函数,令式(a1)、(a2)为零,解得
(a4)
(a5)
对 求一阶和二阶偏导数得:
(a6)
(a7)
因此式(4)是w的凹函数,令式(a6)为零,得式(7),将式(7)代入式(a4)和(a5),得到式(8)和(9)。将(7)~(9)式代入(2)~(5)式得到渠道最大需求和利润。
命题2的证明:不失一般性,令 为零售商边际利润,即,
(a8)
对 求一阶和二阶偏导数得::
(a9)
(a10)
因此式(4)是w的凹函数,由(a8)和(a9)解得
(a11)
分别对 和 求一阶偏导数得:
(a12)
(a13)
由(a12)和(a13)易得Hessian矩阵:
(a14)
因 ,Hessian矩阵负定,式(5)是 、 的凹函数,令式(a12)、(a13)为零,得式(12)和(13)。将式(12)和(13)代入(a11),得(11)。将(11)~(13)式代入(2)~(5)式得渠道最大需求和最大利润。
命题3的证明:零售商的最优反应函数为(a4)和(a5),同样的,制造商的最优反应函数为(a11),同时求解方程(a4)、(a5)和(a11),得到式(15)~(17)。将式(15)~(17)代入式(2)~(5)得到两渠道最大需求和最大利润。
