Operations Research and Fuzziology
Vol.08 No.03(2018), Article ID:26296,6
pages
10.12677/ORF.2018.83013
The Prediction of Effectiveness of Weapons and Combat Based on the Principle of Maximum Entropy
Lei Miao
91049 Force 31 Detachment of the People’s Liberation Army, Qingdao Shandong

Received: Jul. 18th, 2018; accepted: Aug. 1st, 2018; published: Aug. 8th, 2018

ABSTRACT
AHP and fuzzy comprehensive evaluation (FCE) were respectively used for the forecast of the effectiveness of weapons and combat. Then on the basis of merit of maximum entropy principle, the traditional method has been improved, and concluded that the principle of maximum entropy had higher forecast accuracy. Thus it can play a guiding role on the actual operations.
Keywords:Maximum Entropy Principle, Performance Forecast, Evaluation Indicators, Albino Right Function
基于最大熵原理的武器作战效能预测研究
苗磊
解放军91049部队31分队,山东 青岛

收稿日期:2018年7月18日;录用日期:2018年8月1日;发布日期:2018年8月8日

摘 要
分别采用层次分析法(AHP)和模糊综合评判法(FCE)对武器作战效能进行预测。然后在阐述最大熵原理优点的基础上,对传统方法进行了改进,并将得到的结果作了比较,结论证明最大熵原理的预测准确度高于AHP和FCE,对实际作战有一定的指导作用。
关键词 :最大熵原理,效能预测,评价指标,白化权函数

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
准确可信地评估武器作战效能有助于了解、掌握战场态势,明确武器系统的能力和不足,同时可为武器系统的发展、指挥员的作战决策、以及战术使用提供可靠的参考依据 [1] [2] 。
目前,常用的武器系统效能模型是ADC模型 [3] [4] ,该模型由美国空军组织的工业界武器系统效能咨询委员会(WSEIAC)提出,它把武器系统的可靠性、维修性和性能参数等指标效能,综合成为用系统的可用性、可信赖性和系统能力三个综合指标表示的系统效能。但是在实际战场环境中,有很多不确定的客观因素,(比如武器系统的工作环境和使用条件,不同人员对设备的操作熟练度等),要精确评估系统效能是不太可能的事。
本文采用最大熵原理的方法对各种预测模型的结果进行综合,即以各种预测模型的预测结果作为约束,求出最大熵的分布,准确度将大大提高。
2. 武器系统的评价指标
武器系统通常分成三个部分:作战能力系统、控制系统和保障系统。影响武器系统作战效能的主要因素是作战能力系统效能、保障系统效能和武器控制系统效能(见图1)。
确定评价等级
在指标的评价中,将指标的评分等级划分为优、良、中、合格、不合格五个等级,赋予相应的分值为9,7,5,3,1,根据灰色评估理论(GAT)有,确定评价灰类就是要确定评价灰类的等级数、灰类的灰数以及灰数的白化权函数,针对具体对象,通过定性分析确定。本文中5个指标评分等级对应5个评价灰类,其相应的灰数和白化权函数如下 [5] :

Figure 1. Evaluation index system of weapon system effectiveness
图1. 武器系统效能评价指标体系
第一类“优”,即白化权函数 ;
第二类“良”,即白化权函数 ;
第三类“中”,即白化权函数 ;
第四类“合格”,即白化权函数 ;
第五类“不合格”,即白化权函数 。
3. 具体案例分析
3.1. AHP预测武器作战效能 [6]
3.1.1. 构建两两比较判断矩阵A
根据专家经验,对于U1,U2,U3,其A矩阵如表1所示。
3.1.2. 计算判断矩阵的各行元素的积的n (判断矩阵的阶数)次方根
, , ,并将其归一化得到: , , ;
3.1.3. A的满意一致性检验
,其中 为判断矩阵A的最大特征值。判断矩阵A的随机一致性指标 (RI为常数),A具有满意一致性。故U1,U2,U3的指标权重分别为0.6000,0.1000,0.3000。
同理可算出指标U11,U12,U13,U21,U22,U31,U32各自权重分别为:[0.1 0.2 0.7];[0.3 0.7];[0.7 0.3]。
3.1.4. 预测武器作战效能
EAHP = 0.6 * [0.1 0.2 0.7] * [1 10 2]’ + 0.1 * [0.3 0.7] * [2 5]’ + 0.3 * [0.7 0.3] * [5 10]’ = 4.46 (式中的整数矩阵部分可根据判断矩阵,再结合白化权函数得到)。
Table 1. Judgment matrix A
表1. 判断矩阵A
3.2. FCE法预测武器作战效能 [7]
由AHP法已经得知,评判因素集U = [U1,U2,U3] = [0.1 0.2 0.7];其中子因素集U1 = [U11,U12,U13] = [0.6000,0.1000,0.3000];子因素集U2 = [U21,U22] = [0.3 0.7];子因素集U3 = [U31,U32] = [0.7 0.3]。
3.2.1. 确定模糊关系矩阵(根据判断矩阵和白化权函数得到)
模糊关系矩阵如表2~4所示。
3.2.2. 预测武器作战效能
初级评判结果B1 = U1 * R1 = [0.3000 0 0 0.0667 0.6333],
B2 = U1 * R1 = [0.2610 0.1186 0.2004 0.2972 0.1227],
B3 = U1 * R1 = [0.0767 0.0677 0.2947 0.3704 0.1906]。
最终评判结果为:B = U * [B1;B2;B3] = [0.1359 0.0711 0.2464 0.3254 0.2213];
故效能预测值为:Q = B * [9 7 5 3 1] = 4.1503。
3.3. 最大熵原理预测武器作战效能 [7]
3.3.1. 最大熵原理
1948年,香农(Shannon)用熵来定量地描述一个随机事件的不确定性或信息量:
(1)
式中H称为信息熵,熵H是pi的泛函,因此存在一个使H取极大值的分布。相应的概率分布满足
(2)
Table 2. Fuzzy relation matrix R1
表2. 模糊关系矩阵R1
Table 3. Fuzzy relation matrix R2
表3. 模糊关系矩阵R2
Table 4. Fuzzy relation matrix R3
表4. 模糊关系矩阵R3
且若干已知函数 的平均值 是给定的,即:
( ) (3)
我们利用拉格朗日乘子式
(4)
同时联立式(1)~(3)可得
(5)
又由于 ,则
(6)
根据最大熵原理,当且仅当
( )时,H取得最大值 (7)
3.3.2. 预测武器作战效能
由于影响武器作战效能的因素有很多,使得武器在一定程度上呈现出随机和不确定的因素,如果采用单一方法预测,不可避免地产生叫大误差,如果采用最大熵原理的方法对各种预测模型的结果进行综合,即以各种预测模型的预测结果作为约束,求出最大熵的分布,准确度将大大提高。则根据最大熵原理,可以建立如下模型:
(8)
(9)
(10)
联立可求得参数 和 ,进而求得
(11)
最后通过求期望值即可预测出武器的作战效能。则联立(9)~(11)可得:
(12)
(13)
其中y为武器作战效能实际值,这里取7。
由题意可知, , 。
联立(12)和(13)可得到:
, , 则, (14)
最终效能预测值为 。
4. 结果分析
由此可知,AHP法评估的相对误差为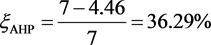 ;FCE法评估的相对误差为
;FCE法评估的相对误差为 ;最大熵原理法评估的相对误差为
;最大熵原理法评估的相对误差为 。综上,最大熵原理法评估的准确度高于AHP法和FCE法。
。综上,最大熵原理法评估的准确度高于AHP法和FCE法。
5. 小结
当影响武器作战效能的因素很多,使得武器在一定程度上呈现出随机和不确定的因素时,可以采用最大熵原理的方法对各种预测模型的结果进行综合,求出最大熵的分布,准确度将大大提高,对实际作战有一定的借鉴作用。
文章引用
苗 磊. 基于最大熵原理的武器作战效能预测研究
The Prediction of Effectiveness of Weapons and Combat Based on the Principle of Maximum Entropy[J]. 运筹与模糊学, 2018, 08(03): 101-106. https://doi.org/10.12677/ORF.2018.83013
参考文献
- 1. 王磊, 吴静, 李旭昌. 基于串并联模型的武器系统作战效能评估[J]. 弹箭与制导学报, 2008, 28(1): 303-306.
- 2. 陈雪娣, 刘峥, 张守宏. 目标闪烁对地空导弹杀伤效能的影响分析[J]. 弹箭与制导学报, 2006, 26(4): 143-146.
- 3. 刘勇, 武昌, 林健. 无线电导航系统作战效能评估研究[J]. 弹箭与制导学报, 2007, 27(5): 268-270.
- 4. 田棣华, 马宝华, 范宁军. 兵器科学技术总论[M]. 北京: 北京理工大学出版社, 2004.
- 5. 朱传志, 孙旭明, 马士友. 基于三角白化权函数的导弹分队信息作战能力评估[J]. 兵工自动化, 2006, 25(6): 9-10.
- 6. 马琳, 宋贵宝, 罗云宝. 导弹武器系统效能评估GAHP模型[J]. 系统仿真学报, 2006, 18(z2): 101-103.
- 7. 林天峰. 基于最大熵原理的网络流量预测综合模型[J]. 微电子学与计算机, 2006, 23(8): 147-149.
