Operations Research and Fuzziology
Vol.
09
No.
04
(
2019
), Article ID:
32821
,
6
pages
10.12677/ORF.2019.94032
Online Scheduling Problem for Jobs Arriving over Time on Related Machines
Lina Ma1,2, Rongheng Li1*
1Key Laboratory of High Performance Computing and Stochastic Information Processing, College of Mathematics and Statistics, Hunan Normal University, Changsha Hunan
2The First Middle School of Yuanling County, Huaihua Hunan

Received: Oct. 15th, 2019; accepted: Oct. 29th, 2019; published: Nov. 5th, 2019

ABSTRACT
Online scheduling problem for jobs arriving over time is as follow. We are given m related machines with the processing speed of , respectively and a job list arriving over time. The objective function is to minimize the maximum completion time of all machines. In this paper, LS algorithm is considered for online scheduling problem for jobs arriving over time under the assumption , . The worst performance ratio of the LS algorithm is given and proved.
Keywords:Scheduling Problem, Related Machine, LS Algorithm, Worst Performance Ratio

同类机上工件实时到达在线排序问题
马丽娜1,2,李荣珩1*
1计算与随机数学教育部重点实验室 湖南师范大学数学与统计学院,湖南 长沙
2沅陵县第一中学,湖南 怀化

收稿日期:2019年10月15日;录用日期:2019年10月29日;发布日期:2019年11月5日

摘 要
同类机上工件实时到达的在线排序问题是给定m台分别具有加工速度 的同类机器 及实时到达的工件序列 ,目标函数是最小化机器的最大完工时间,本文研究了 , 时同类机上工件实时到达的在线排序问题的LS算法,给出并证明了LS算法的最坏性能比。
关键词 :排序问题,相关平行机,LS算法,最坏性能比

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
同类机排序问题是将n个独立工件 分配到m台具有相同功能的机器 上加工,每台机器 的加工速度为 ,不妨假设 ,每个工件只需在其中一台机器上加工一次就能完工,每台机器每次只能加工一个工件。工件 之间没有先后的依存关系,
且 的大小为 ,工件 安排在机器 上加工时所需的时间为 ,目标函数是使所有
工件在最早时间内完成加工,也就是使得所有机器中最大完工时间达到最小。该问题由Gonzalez [1] 等人首先提出。当 时称为相同平行机排序问题,相同平行机排序问题首先由Graham [2] 提出。根据排序者对工件信息的了解程度,排序问题分为离线和在线两种情形,离线情形是指在安排工件前,所有工件信息都已知道,包括工件大小及到达时间等,在线情形是指工件是逐个释放的,只有在当前出现了的工件被安排后下一个工件的信息才能释放。Granham [2] 首先研究了相同平行机在线排序问题,
给出了LS算法并证明了LS算法具有最坏性能比 。LS是指总是安排当前工件在能使这个工件最早
完工的机器上。Cho和Sahni [3] 首先研究了同类机在线排序问题,得到了 时LS算法的最坏性能比
时LS算法的最坏性能比
为 , 时最坏性能比为 ,当 , , 时最坏性能比为 。Berman等 [4] 得到最坏性能比为 ,并证明了问题的下界为≈4.311。此外,关于机器数m取较小的值时,也有一些结果。例如:当 时,Epstein等 [5] 证明了LS是最好的在线算法,其最坏性能比为 ,这里的s为加工速度较快的机器与加工速度较慢的机器两者的加工速
度的比值。当 时,蔡 [6] 证明了当 , 这一特殊情形下LS算法的最坏性能比。Cai和Yang [7] 也研究了当 时的情形,证明了部分情形下LS算法是最好的在线算法。
经典排序问题假设机器开始加工时所有工件都已到达,但实际情况中工件不一定都已到达,所以提出了工件有到达时间的排序问题。有到达时间的在线问题又分为实时到达在线问题和订单到达在线问题。设工件序列 中 的到达时间为 ,如果 为任意实数序列,则称其为订单在线排序问题或工件有任意到达时间排序问题 [8],当 时我们称其为工件实时到达在线排序问题。易知工件实时到达在线排序问题是订单在线排序问题的特例。文献 [8] 中只讨论相同平行机的订单在线排序问题,即 的情形。本文是首次讨论同类平行机的实时到达在线排序问题。
2. 符号及LS算法
我们后面所要引入的符号的的意义如下:
1) Ui表示在 LS 算法下机器 上面的空闲时间总和。
2) rj和pj分别表示工件Jj的到达时间和工件大小。
3) 表示在OPT算法下机器的最大完工时间。
4) 表示在LS算法下机器的最大完工时间。
5) Hi表示在LS算法下安排最后一个工件Jn之前机器 的完工时间。
6) Fi表示在LS算法下安排完所有的工件后机器 的最后完工时间。
定义1:算法A是一个近似算法, 和 分别表示在算法A和最优算法下该工件序列的最大完工时间。我们定义
为算法A的最坏性能比,其中 为任一符合条件的工件序列。
本文后面我们总是假设m台具有相同功能的机器
的加工速度为
, 。下面给出LS算法:
。下面给出LS算法:
LS算法:
设当前工件是
,大小为
及到达时间为
,各个机器当前的完工时间为
,我们将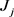 安排在机器
上,这里
满足如下条件:
安排在机器
上,这里
满足如下条件:
(1)
即算法总是安排当前工件 在能使这个工件最早完工的机器上。
如果(1)中有
,则
在机器
上产生空闲,空闲长度为
。下面给出一个实例说明LS算法的应用。设
, ,
,,,,,,, 。显然J1被安排在机器M2的[1, 3]时间段上加工,而J2被安排在机器M1的时间段[1, 2]上加工。J3安排在M1上的起始时间为2,完工时间为6,安排在M2上的起始时间为3,完工时间为5,故按LS算法规则,J3应安排在M2上。
,
,,,,,,, 。显然J1被安排在机器M2的[1, 3]时间段上加工,而J2被安排在机器M1的时间段[1, 2]上加工。J3安排在M1上的起始时间为2,完工时间为6,安排在M2上的起始时间为3,完工时间为5,故按LS算法规则,J3应安排在M2上。
LS算法中每个工件的安排需要找出最早完工的机器,机器台数为m,最多m次可以找出,注意到工件个数为n,所以复杂度为O(mn)。
下面我们分析LS算法的最坏性能比。
3. 定理及其证明
对给定的工件序列 ,我们首先给出下面的基本不等式:
引理1: 。
。
证明:由基本不等式知有 ,,所以有 。
定理 2:如果 , ,则实时在线LS算法有性能比:
证明:我们不妨设Jn的完工时间即为 ,由LS算法,我们有
, ,
所以
上面第二个不等式由引理1得。
当 时 即有:
当 时,由于 ,所以有
因而得到
(2)
下面我们假设工件t′是最后一个被 LS 算法安排在机器Mm上加工但在OPT算法下没有安排在Mm上的工件的长度。如果这样的t′不存在,则有 。如果Jn在OPT算法下安排在机器Mm上,则有
。
否则Jn在OPT算法下安排在某一机器 上,这时有 ,并且
。
现在我们假设存在这样的t′,设 表示工件t′之后在机器Mm上加工的工件总长度。显然 且 。假设在LS算法下工件t′之后Mm上还有空闲,则在OPT算法下从Mm移走工件t′之后不会改变Mm的完工时间,所以 。分别讨论最优算法里Jn安排在机器Mm上与不在机器Mm上,我可以用t′不存在时同样的方法可得
。
假设在LS算法下工件t′之后Mm上没有空闲,由LS算法知
。
如果Jn在OPT算法下安排在机器Mm上,则
。
所以
整理得
。
若Jn在OPT算法下没有安排在Mm上,则有 并且有
。
所以不管什么情况都有
。
对于Mm有 ,所以
结合(2)定理得证。
4. 小结
本文研究了特殊情形下在同类机上工件实时到达的在线排序问题的LS算法,给定m台同类机器
,机器加工速度假设为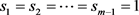 ,
时,目标函数是最小化机器的最大完工时间,我们给出了LS算法的最坏性能比为
,
时,目标函数是最小化机器的最大完工时间,我们给出了LS算法的最坏性能比为
进一步的研究可设计比LS算法具有更好性能比的算法。
基金项目
本文得到湖南省教育厅重点课题(编号:16A126)资助。
文章引用
马丽娜,李荣珩. 同类机上工件实时到达在线排序问题
Online Scheduling Problem for Jobs Arriving over Time on Related Machines[J]. 运筹与模糊学, 2019, 09(04): 279-284. https://doi.org/10.12677/ORF.2019.94032
参考文献
- 1. Gonzalez, T., Ibarra, O.H. and Sahni, S. (1977) Bounds for LPT Scheduling on Uniform Processors. SIAM Journal on Computing, 6, 155-166. https://doi.org/10.1137/0206013
- 2. Graham, R.L. (1969) Bounds on Multiprocessing Timing Anomalies. SIAM Journal on Applied Mathematics, 17, 416-429. https://doi.org/10.1137/0117039
- 3. Cho, Y. and Sahni, S. (1980) Bounds for List Schedules on Uniform Pro-cessors. SIAM Journal on Computing, 9, 91-103. https://doi.org/10.1137/0209007
- 4. Berman, P., Chanrikar, M. and Karpinski, M. (2000) Online Load Balancing for Related Machines. Journal of Algorithms Archive, 35, 108-121. https://doi.org/10.1006/jagm.1999.1070
- 5. Epstein, L., Noga J., Seiden, S., Sgall, J. and Woeginger, G.J. (2001) Randomized Online Scheduling on Two Uniform Machines. Journal of Scheduling, 4, 71-92. https://doi.org/10.1002/jos.60
- 6. 蔡圣义. 三台同类机在线排序问题一种特殊情形的研究[J]. 系统工程理论与实践, 2006, 26(7): 41-46.
- 7. Cai, S.Y. and Yang, Q.F. (2012) Online Scheduling on Three Uniform Machines. Discrete Applied Mathematics, 160, 291-302. https://doi.org/10.1016/j.dam.2011.10.001
- 8. Li, R.H. and Huang, H.C. (2004) On-line Scheduling for Jobs with Arbitrary Release Times. Computing, 73, 79-97. https://doi.org/10.1007/s00607-004-0067-1
NOTES
*通讯作者。