Hans Journal of Data Mining
Vol.06 No.04(2016), Article ID:18806,11
pages
10.12677/HJDM.2016.64019
Analysis of Beijing PM2.5 Concentration Effect Factors Based on Generalized Additive Models
Xiaotong Li*, Mo Zhang
College of Science, China University of Petroleum (Beijing), Beijing

Received: Oct. 8th, 2016; accepted: Oct. 24th, 2016; published: Oct. 27th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In recent years, air pollution in Beijing is increasingly serious; PM2.5 has caused widespread concern in the community. There are obvious limitations about influencing factors’ type and model selection in current studies on the influence factors of PM2.5 concentration in Beijing. Based on the above two points, this paper conducted a generalized additive model which regarded PM2.5 concentration as response variable and influence factors as predictor variable, and the results showed that: the factors influencing PM2.5 concentration include NO2 concentration, wind speed, temperature, month, CO concentration, O3 concentration and humidity. This paper also conducted a linear regression model in order to make contrast, and the results showed that the goodness of fit of the additive model is much better than the linear model.
Keywords:PM2.5 Concentration, Generalized Additive Model, Linear Regression Model

基于广义加性模型的北京市PM2.5浓度影响 因素分析
李晓童*,张默
中国石油大学(北京)理学院,北京

收稿日期:2016年10月8日;录用日期:2016年10月24日;发布日期:2016年10月27日

摘 要
近年来,北京的空气污染日趋严重,PM2.5也引起了社会各界的广泛关注。目前针对北京市PM2.5浓度影响因素的研究中,在影响因素种类和模型选择方面有明显的局限性。文章基于上述两点,建立了以PM2.5浓度为响应变量、影响因素为预测变量的广义加性模型,结果发现PM2.5浓度的影响因素包括NO2浓度、风速、温度、月份、CO浓度、O3浓度和湿度。文章还建立了线性回归模型进行对比,结果发现加性模型的拟合效果明显优于线性模型。
关键词 :PM2.5,广义加性模型,线性回归模型

1. 引言
北京的空气污染十分严重,PM2.5作为主要的空气污染物之一,对人体健康有极大危害,因此研究如何控制PM2.5污染是十分必要的。国内关于PM2.5浓度影响因素的研究中,考虑的影响因素主要包括时间、空间、气象条件和前体物等。云慧(2013)等对深圳PM2.5的时空分布特征进行了研究 [1] 。陈云进(2015)等研究了昆明市PM2.5浓度与气象因素之间的关系 [2] 。贾艳红(2016)等研究了PM2.5与PM10、CO、NO2、SO2之间的微妙关系 [3] 。从模型选择方面来看,绝大多数研究者选择用传统的线性回归模型来分析PM2.5浓度的影响因素。张人禾(2013)等通过建立多元线性回归模型来分析气象条件对PM2.5浓度的影响,结果发现气象因子可以解释PM2.5浓度68%的变化 [4] 。
综上所述,现有研究存在两个明显的局限性:一方面,对PM2.5浓度影响因素的选择很是单一,缺乏全面系统的观察分析;另一方面,模型的选择囿于传统的线性回归模型,模型拟合效果不好。为克服现有研究的局限性,本文同时选择时间、气象条件和前体物这三类影响因素作为自变量,对PM2.5浓度影响因素进行更加全面系统的分析,模型选择擅长处理非线性关系的广义加性模型,突破了传统线性模型对变量的线性假定。本文安排如下:
第一节是引言;第二节介绍了广义加性模型的理论知识;第三节至第五节是实证分析,分别建立了线性回归模型和广义加性模型来研究北京市PM2.5浓度的影响因素,并对两个模型进行了多角度的对比;第六节是总结,首先对研究工作的优缺点进行了总结,然后提出了一些治理雾霾的建议和措施。
2. 广义加性模型
近年来,非参数模型受到越来越多学者的关注。Stone (1985年)提出了标准的加性模型(additive model),模型中的每一个加性项都使用单独的光滑函数来估计,避免了“维度祸根”问题 [5] 。Hastie和Tibshirani (1990年)将加性模型的技术应用于广义线性模型(generalized linear model, GLM),于是就产生了广义加性模型(generalized additive model, GAM),广义加性模型是加性模型的推广,本质是利用连接函数把加性模型中响应变量的期望与加性部分联系起来 [6] 。
广义加性模型的公式如下:
 (1)
(1)
其中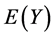 是
是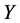 的期望,
的期望, 是截距,
是截距,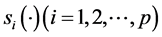 是非参数光滑函数,满足
是非参数光滑函数,满足 ,光滑函数
,光滑函数 是针对每一个预测变量
是针对每一个预测变量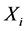 的单变量函数,它可以是光滑样条函数、局部回归光滑函数或核函数等,本文使用的光滑函数是三次样条函数,它不仅具有较好的整体光滑性,还能很好地适应数据和函数的变化。
的单变量函数,它可以是光滑样条函数、局部回归光滑函数或核函数等,本文使用的光滑函数是三次样条函数,它不仅具有较好的整体光滑性,还能很好地适应数据和函数的变化。
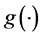 为连接函数,它是一个单调可微的非线性函数,对于不同分布类型的因变量,连接函数的形式也不同,其具体对应关系如下:
为连接函数,它是一个单调可微的非线性函数,对于不同分布类型的因变量,连接函数的形式也不同,其具体对应关系如下:
 (2)
(2)
事实上,如果模型中的每一项都用非参数回归来拟合的话,往往会出现计算量大、过度拟合等问题,并且参数形式也有利于解释响应变量与预测变量之间的关系,所以在模型中不必所有项都是非线性的,我们可以纳入线性项来缓解上述问题,这样就出现了半参数广义加性模型,其表达式为:
 (3)
(3)
广义加性模型的求解有很多种方法,本文介绍的方法是SAS软件里GAM过程使用的方法,也是目前最主流的求解方法。具体求解过程见表1。
局部积分算法的具体计算过程如下:
1) 赋初值
 ,
, ,
,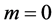
2) 迭代过程 
① 根据上一次迭代构造校整响应变量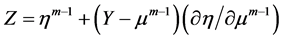 ,
,
其中 ,
, 。
。
② 构造权重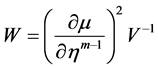 。
。
③ 利用加权backfitting算法求解以Z为响应变量的加性模型,我们将得到各光滑加性项的估计值。
3) 重复2)直到 不再减少,其中
不再减少,其中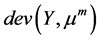 指估计值
指估计值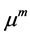 的离差。
的离差。
其中 是
是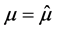 处
处 的方差,算法2)中用的是带权重的backfitting算法,数据首先用权重做转换,之后对转换的数据应用backfitting算法 [7] 。
的方差,算法2)中用的是带权重的backfitting算法,数据首先用权重做转换,之后对转换的数据应用backfitting算法 [7] 。
Backfitting算法的具体过程如下:
1) 初始化
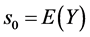 ,
, ,
,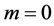
2) 迭代过程 ,
,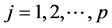
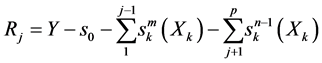
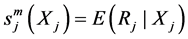
Table 1. Algorithmic process
表1. 算法流程
直到 不再减小,迭代停止。
不再减小,迭代停止。
在上述示例中 代表
代表 在第m次迭代中的估计。注意到通过一开始有效地集中Y,我们保证了在每种情况下都有
在第m次迭代中的估计。注意到通过一开始有效地集中Y,我们保证了在每种情况下都有 。显而易见的是RSS在算法的任何一步都是不增加的所以算法收敛。
。显而易见的是RSS在算法的任何一步都是不增加的所以算法收敛。
在估计非线性光滑函数的光滑参数时,本文选用的方法是广义交叉验证。广义交叉验证函数被定义为: ,其中
,其中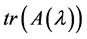 是指矩阵
是指矩阵 的迹,即矩阵对角线元素之和,在本文中,我们以最小化的GCV作为选取光滑参数的标准。当确定了光滑参数之后,本文采用惩罚最小二乘法来估计三次样条函数。惩罚最小二乘法是一种典型的粗糙度惩罚方法,其惩罚平方和为:
的迹,即矩阵对角线元素之和,在本文中,我们以最小化的GCV作为选取光滑参数的标准。当确定了光滑参数之后,本文采用惩罚最小二乘法来估计三次样条函数。惩罚最小二乘法是一种典型的粗糙度惩罚方法,其惩罚平方和为: ,使
,使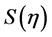 最小的
最小的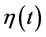 就是曲线的最小二乘估计
就是曲线的最小二乘估计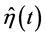 。显然,
。显然,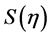 综合考虑了曲线的拟合优度和拟合光滑度,拟合优度采用残差平方和
综合考虑了曲线的拟合优度和拟合光滑度,拟合优度采用残差平方和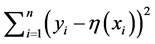 度量,曲线光滑度则用
度量,曲线光滑度则用 度量。光滑参数 决定了曲线的光滑度,如果 较大,则
度量。光滑参数 决定了曲线的光滑度,如果 较大,则 中的主要影响部分为粗糙度惩罚项
中的主要影响部分为粗糙度惩罚项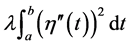 ,所以估计函数
,所以估计函数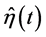 的曲率较小,光滑度好;相反,如果
的曲率较小,光滑度好;相反,如果 较小,则
较小,则 中的主要影响部分为残差平方和,
中的主要影响部分为残差平方和, 与数据点接近,曲线凹凸不平。
与数据点接近,曲线凹凸不平。
3. 变量的选取
本文主要研究北京市PM2.5浓度的影响因素,时间跨度选择为2015年1月1日至12月31日,时间分辨率为每日。本文的数据来源于青悦环境数据中心(https://wat.epmap.org)和TuTiempo网站(http://en.tutiempo.net)。
下面介绍回归模型中各变量的选取:
1) 响应变量
本文选取PM2.5浓度的自然对数作为响应变量,在数据集中用 表示。本文假定 服从正态分布,其频率分布直方图如见图1。
2) 预测变量
本文选取的预测变量涵盖了时间、气象条件、前体物这三大类因素,对PM2.5浓度影响因素的考虑较为全面。
本文把月份作为时间变量考虑为PM2.5浓度的影响因素,在数据集中用 表示。气象因素是影响PM2.5浓度的重要环境因素,本文考虑的气象条件包括日平均温度、日最高温度、日最低温度、湿度、降水量、日平均风速、日最大风速和日平均海平面大气压,其单位分别是℃、℃、℃、%、mm、Km/h、Km/h、Kpa,在数据集中分别用tave、tmax、tmin、humid、rainfall、wind、windmax、slp表示。
PM2.5中的有机碳主要来源于 ,而无机盐则主要是通过空气中的SO2、NO2等污染物进行光化学

Figure 1. Lnpm histogram
图1. Lnpm的直方图
反应生成,因此气态污染物和大气的氧化性对PM2.5浓度有较大影响。本文将气态污染物CO、SO2、NO2的浓度考虑为PM2.5浓度的影响因素,单位分别为mg/m3、mg/m3、mg/m3,在数据集中分别用CO、SO2、NO2表示;大气氧化性的衡量有两种标准:臭氧O3或者OX(O3 + NO2),为了不遗漏数据,本文将两者都考虑进去,其单位都是mg/m3,在数据集中,o31、o32分别代表臭氧O3的日最高一小时平均值和日最高八小时滑动平均值,oxi1、oxi2分别代表OX(O3 + NO2)的日最高一小时平均值和日最高八小时滑动平均值。
4. 建立广义加性模型
本文在选取变量时假定响应变量是服从正态分布的,所以广义加性模型的连接函数选择单位连接,单位连接的广义加性模型实际上就是普通的加性模型 。
。
本章建立加性模型的具体步骤如表2所示。
下面开始用SAS软件中的The GAM Procedure建立加性模型:
由于SAS中的GAM过程里不提供变量选择的方法,本文采取人工剔除变量的方法,剔除标准为变量的显著性和其光滑参数值,显著性水平取0.05,光滑参数最低限值为0.5。用后向剔除法选择变量的步骤如见表3所示。
在Step4中所有变量的线性部分和非线性部分都显著,光滑参数都大于0.5,GCV值也很低说明拟合优度很好,这就是本文通过后向剔除法最终确定的模型。模型求解结果如表4~表6所示。
加性模型需要验证的假定只有残差,经验证,模型的残差图及其QQ图都是符合假定的,加性模型的结果有效。下面用同样的方法对加性模型进行评价, 的观测值与拟合值的线性回归模型求解如表7所示。
总体来说,模型拟合效果很好,MSE、AIC、BIC值很小,确定系数 达到了87.70%,说明该模型能够解释响应变量87.70%的变化。
为了进一步验证模型的准确性,利用该模型对2016-1-1至2016-1-7这一个星期里的lnpm值进行预测(利用R软件),预测值与真实值的对比图如图2所示。
观察图2发现,GAM预测值与真实值很相近,除了第七天相差稍大以外,在其余时间预测值与真实值的差别都在0.5个单位以内,这说明加性模型拟合效果很好,经计算其绝对误差平方和为1.105,模型通过了评价,最终选择此模型来解决问题。
Table 2. The steps of building model
表2. 建立模型的步骤
Table 3. The steps of BE
表3. 后向剔除法的步骤
Table 4. Parameter estimates
表4. 参数估计
Table 5. Fit summary for smoothing components
表5. 非参数拟合
Table 6. Analysis of deviance
表6. 离差分析
Table 7. Goodness of fit
表7. 拟合优度表
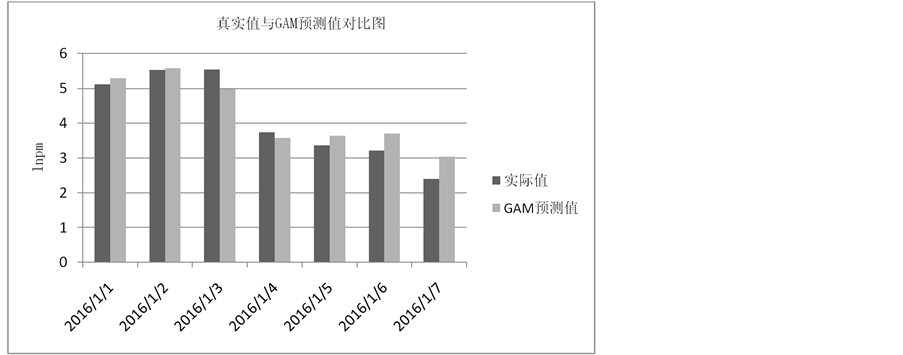
Figure 2. Table of comparison between real value and GAM prediction value
图2. 真实值与GAM预测值的对比表
最终得到的半参数加性模型为:
从模型可以看出:PM2.5浓度的影响因素有月份、NO2浓度、CO浓度、O3日最高八小时滑动平均浓度、日最高温度、湿度、日最大风速。NO2浓度的回归系数为0.01787,说明PM2.5浓度与NO2浓度呈正相关;日最高温度和日最大风速的回归系数分别是−0.00644和0.01302,这说明PM2.5浓度与日最高温度呈负相关,与日最大风速呈正相关。因为SAS中的GAM过程自动将非参数回归中的线性部分分离出来,所以对于进行非参数回归的o32、humid、month、co这4个变量而言,线性项与非线性项的加和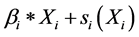 才是它们对响应变量的完整预测,为了更直观地观察,下文用图像来表示非参数回归变量对PM2.5浓度的影响效果(见图3~图6)。
才是它们对响应变量的完整预测,为了更直观地观察,下文用图像来表示非参数回归变量对PM2.5浓度的影响效果(见图3~图6)。
从图3~图6可以看出,当空气中湿度等于35%、臭氧浓度等于40 mg/m3时,PM2.5浓度达到最小值;PM2.5浓度的变化规律有明显的季节趋势,春冬季较高,夏秋季较低;从整体上来看, 浓度与PM2.5浓度是呈正相关的。
5. 模型比较
为了找到最适合处理PM2.5浓度影响因素问题的模型,本文还建立了相应的线性回归模型用作对比分析,线性模型的求解结果见表8。
表中的no23、co3、o323分别代表NO2、CO、o32的三次方,经验证,线性模型符合其模型假定。下面将从拟合优度和预测效果这两个角度对本文建立的广义加性模型和线性回归模型进行比较。
前文对广义加性模型进行评价时建立了响应变量Y的观测值与拟合值的线性回归模型,在这里依然用这种方法对两个模型的拟合优度进行比较。相关指标如表9所示。
从表9可以看出,加性模型的确定系数 比线性回归模型的大0.0910,这意味着可以多解释响应变

Figure 3. On the prediction of ozone concentration
图3. 关于臭氧浓度的预测图

Figure 4. The forecast of humidity
图4. 关于湿度的预测图
量9.10%的变化,这种差距是非常大的,对问题的解决影响很大;加性模型的AIC、BIC比线性回归模型的小200多;加性模型的MSE仅是线性模型MSE的57%。以上各项都说明加性模型的拟合优度比线性回归模型好很多。
为了进一步比较两个模型的准确性,本文分别用两个模型对2016-1-1至2016-1-7这一个星期里lnpm值进行预测,其预测值与真实值对比图如图7所示。
观察图7发现,REG预测值与真实值差距较大,基本相差在一个单位左右,而GAM预测值与真实值很相近,基本相差都在0.5个单位以内,经计算发现REG过程的绝对误差平方和4.978是GAM过程绝对误差平方和1.105的将近五倍,以上都说明加性模型拟合优度明显比线性模型更好。
6. 总结
为分析北京市PM2.5浓度的影响因素及其影响形式,本文建立了以PM2.5浓度为响应变量、影响因

Figure 5. Forecast of the month
图5. 关于月份的预测图
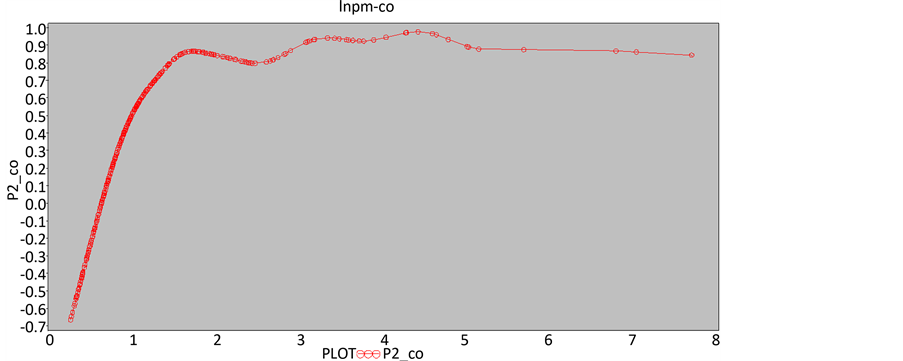
Figure 6. The prediction of CO concentration
图6. 关于CO浓度的预测图
Table 8. Parameter estimates
表8. 参数估计
Table 9. Goodness of fit
表9. 拟合优度表

Figure 7. Table of comparison between the real value and the predicted value of the two models
图7. 真实值与两个模型预测值的对比表
素为预测变量的广义加性模型,其优点主要有三个:
1) 克服了现有研究中影响因素和模型选择的局限性:现有研究一般都是简单地以时间、气象条件或前体物中的一类作为自变量,而本文同时选取了这三类影响因素作为自变量,更加全面;常用的线性模型忽略了实际数据不满足线性假定的事实,而本文建立的广义加性模型不需要有线性假设,更适合空气质量领域的数据分析。
2) 模型拟合优度好,能解释PM2.5浓度87.70%的变化。本文建立的广义加性模型其AIC值达到了−816,MSE达到了0.1063,且模型对2016年的预测值十分准确,以上都说明了该模型的拟合优度好,很适合处理本文中的数据。
3) 首次将后向剔除法与模型半参数化调整相结合,在保证拟合优度的同时,也确保了拟合曲线的光滑度。本文使用的后向剔除法以显著性和光滑参数为标准,对不符合标准的变量不是简单地剔除,而是对其进行参数估计,这样处理保证了拟合的优度和光滑度,也避免了计算量大、过度拟合的问题,同时其参数部分也更便于解释,可谓一石三鸟。
本文建立的广义加性模型同样存在其不足:没有考虑非参数回归中的共曲线性问题 [8] ,可能会使模型的误差变大;变量选择采用人工方式不够精确,可以继续深入研究非参数回归中的变量选择方法;光滑函数仅尝试了样条函数,可以进一步深入探讨局部回归函数和薄板样条函数的应用。
本文的研究结果显示前体物NO2和CO是影响PM2.5浓度的重要因素,因此控制和管理NO2和CO的排放至关重要。NO2主要来源于垃圾焚烧、化石燃料的燃烧和机动车尾气,CO则主要来源于机动车尾气和燃料的不充分燃烧。相关部门可以从加强生态文明建设、垃圾回收再利用、推广清洁能源、科学用煤等方面进行雾霾治理。
文章引用
李晓童,张 默. 基于广义加性模型的北京市PM2.5浓度影响因素分析
Analysis of Beijing PM2.5 Concentration Effect Factors Based on Generalized Additive Models[J]. 数据挖掘, 2016, 06(04): 168-178. http://dx.doi.org/10.12677/HJDM.2016.64019
参考文献 (References)
- 1. 云慧, 何凌燕, 黄晓锋, 等. 深圳市PM2.5化学组成与时空分布特征[J]. 环境科学, 2013, 34(4): 1245-1251.
- 2. 陈云进, 王劲. 基于监测统计的昆明PM2.5主要来源与污染气象因素分析[J]. 环境科学导刊, 2015(1): 37-44.
- 3. 贾艳红, 陆赛娣, 冯小莉, 等. 中国雾霾分布及其组成相关性分析[J]. 测绘与空间地理信息, 2015(12): 9-12.
- 4. 张人禾, 李强, 张若楠. 2013年1月中国东部持续性强雾霾天气产生的气象条件分析[J]. 中国科学: 地球科学, 2014, 44(1): 27-36.
- 5. Stone, C.J. (1985) Additive Regression and Other Nonparametric Models. Annals of Statistics, 13, 689-705. http://dx.doi.org/10.1214/aos/1176349548
- 6. Hastie, T. and Tibshirani, R. (1986) Generalized Additive Models. Statistical Science, 1, 297-310. http://dx.doi.org/10.1214/ss/1177013604
- 7. 罗丹. 中国国债超额回报率的拟合和预测[D]: [硕士学位论文]. 湘潭: 湘潭大学,2014.
- 8. 贾彬, 王彤, 王琳娜, 等. 广义可加模型共曲线性及其在空气污染问题研究中的应用[J]. 第四军医大学学报, 2005, 26(3): 280-283..
