Hans Journal of Data Mining
Vol.
08
No.
04
(
2018
), Article ID:
27016
,
15
pages
10.12677/HJDM.2018.84020
An Overview of Deep Learning Optimization Methods and Learning Rate Attenuation Methods
Yuxu Feng, Yumei Li
School of Science, Beijing Technology and Business University, Beijing

Received: Sep. 7th, 2018; accepted: Sep. 22nd, 2018; published: Sep. 29th, 2018

ABSTRACT
As an important technology in the field of machine learning, deep learning has been mature in image recognition, machine translation, natural language processing and other fields, and it has been achieved many good results. In this paper, the development of deep learning model optimizers is analyzed, and the commonly methods such as gradient descent, gradient descent of momentum, Adagrad, RMSProp, Adadelta, Adam, Nadam and ANGD are introduced. The attenuation mode of learning rate is summarized as piecewise constant attenuation, polynomial attenuation, exponential attenuation, natural exponential attenuation, cosine attenuation, linear cosine attenuation and noise linear cosine attenuation. The existing problems and future development trend of deep learning are described, which provide relatively complete learning materials and literature support for the researchers who are engaged in deep learning.
Keywords:Deep Learning, The Optimizer, Gradient Descent, Adagrad, RMSProp, Adadelta, Adam, Learning Rate Attenuation
深度学习优化器方法及学习率衰减 方式综述
冯宇旭,李裕梅
北京工商大学理学院,北京

收稿日期:2018年9月7日;录用日期:2018年9月22日;发布日期:2018年9月29日

摘 要
深度学习作为现今机器学习领域中的重要的技术手段,在图像识别、机器翻译、自然语言处理等领域都已经很成熟,并获得了很好的成果。文中针对深度学习模型优化器的发展进行了梳理,介绍了常用的梯度下降、动量的梯度下降、Adagrad、RMSProp、Adadelta、Adam、Nadam、ANGD等优化方法,也对学习率的衰减方式有分段常数衰减、多项式衰减、指数衰减、自然指数衰减、余弦衰减、线性余弦衰减、噪声线性余弦衰减等方法进行了总结,对深度学习现阶段存在的问题以及对未来的发展趋势进行了阐述,为入门深度学习的研究者提供了较为完整的最优化学习材料以及文献支持。
关键词 :深度学习,优化器,梯度下降,Adagrad,RMSProp,Adadelta,Adam,学习率衰减

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
几十年来,人工智能一直是公众的热点话题。从20世纪50年代开始,人们一直希望,基于逻辑、知识表示、推理和计划的经典人工智能技术将产生革命性的软件,它可以理解语言,控制机器人,并提供专家建议。随着大数据时代的到来,深度学习技术已经成为研究中的热点,深度学习的发展为人工智能的实现提供了很大的帮助,不论是推荐系统、图像识别、机器翻译等,都已获得很大的成功。但是这些系统的实现,都是基于深度神经网络模型的建立及训练,它同时也伴随着最小化损失函数的目标,故而如何寻找到最小值或极小值成为优化模型的一个重点。
当研究者试图提高深度学习系统的性能时,大致可以从三个方面入手解决。第一是提高模型的结构,比如增加神经网络的层数,或者将简单的神经元单位换成复杂的LSTM神经元 [1] ,比如在自然语言处理领域内,利用LSTM模型挖掘语法分析的优势 [2] 。第二个方法是改进模型的初始化方式,保证早期梯度具有某些有益的性质 [3] ,或者具备大量的稀疏性 [4] ,或者利用线性代数原理的优势 [5] 。最后的方法就是选择更强大的学习算法,比如对度梯度更新的方式 [6] ,也可以是采用除以先前梯度L2范数来更新所有参数 [7] ,甚至还可以选用计算代价较大的二阶算法 [8] 。
在梯度下降中,原始算法是使用给定的学习率,全局进行更新参数。在最优化的初期,学习率可以大一点,让参数以较大的步伐进行更新,在后期则需要减小学习率,以免较大步长越过最优值,而来回动荡。故而研究者对学习率有了新的更新方式,甚至是自适应学习率。
本文就将针对模型优化器的方法梯度下降、动量的梯度下降、Adagrad、RMSProp、Adadelta、Adam、Nadam等方法以及学习率的衰减方式分段常数衰减、多项式衰减、指数衰减、自然指数衰减、余弦衰减、线性余弦衰减、噪声线性余弦衰减等研究进行了系统的梳理,并对深度学习发展存在的问题进行了分析,以及对未来的发展进行了展望,有助于刚入门深度学习的研究者系统地学习,对进一步优化方法的研究及应用也奠定了一定的基础。
2. 梯度下降法
样本数据为 , ,共有m个样本。其中样本的输入部分 为数据的n个特征。步长(learning rate)是在迭代过程中,决定了沿梯度负方向前进的长度。
在监督学习中,为了拟合输入样本,使用假设函数(hypothesis function),记为 , ,为方便写,加入 ,则 。
机器学习中,为了评估模型拟合的好坏,一般用损失函数(loss function)来度量拟合的好坏,损失函数极小化,也就是拟合的最好,对应的模型参数也将是最优参数。通常将样本输出与假设函数差的平方作为损失函数,即 。
下面将对梯度下降以及各种衍生算法分别进行阐述。
2.1. 梯度下降(GD)算法
在机器学习中,最小化损失函数时,常采用梯度下降法一步步迭代去趋近全局最优值。当然,如果损失函数是非凸函数,梯度下降法最后可能得到的是局部最优解,但如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解。
梯度下降 [9] 是一种简单的、众所周知的且非常健壮的优化算法,它通过计算参数的梯度,并通过与学习率作乘,减去了该梯度的一部分进行参数更新。
可以看到,当学习率 取值比较小时,参数更新的会比较慢,则导致收敛到极值的速度较慢;若把学习率设置的较大时,易导致在搜索过程中来回震荡,故而如何设置学习率的大小、如何加快收敛的速度以及如何减小搜索过程中的震荡才是深度学习真正要解决的问题之一。
2.2. 梯度下降法的延伸
梯度下降方法作为很稳健的优化方法,一直被广为使用,研究者为此做出了一些延伸方法,主要有批量梯度下降法、随机梯度下降法、小批量梯度下降法等。
批量梯度下降法 [10] (Batch Gradient Descent),它是在梯度下降的算法基础上,在梯度更新的时候采用全部样本进行更新参数 ,更新规则即为式(1)。
(1)
随机梯度下降法 [11] (Stochastic Gradient Descent),它与批量梯度下降法的不同是在于梯度更新参数的时候仅随机选取一个样本进行更新,并非全部样本, 更新规则即为式(2)。
(2)
从式(1)和式(2)可以看出,这两个方法相当于两个极端,一个是采用了全部的样本数据来进行更新参数,而随机梯度下降仅选取一个样本数据来进行更新参数,优缺点也显而易见,批量梯度下降的训练速度要慢,随机梯度下降的训练速度明显要快,特别是在大样本数据量下,批量梯度下降的时间成本会很高,不可取。但是从准确度来讲,随机梯度下降仅选取一个样本数据就决定梯度方向,会导致迭代的方向变化很大,不能很快收敛到局部最优解处,也可能导致解不是最优的。
基于上述两种方法,就诞生了小批量梯度下降。
小批量梯度下降法(Mini-batch Gradient Descent),是批量梯度下降法和随机梯度下降法的折衷,也就是对于m个样本,采用x个样本来迭代,1 < x < m,更新规则即为式(3)。
(3)
小批量梯度下降兼顾了二者的优缺点,相比批量梯度下降,加快了收敛速度,相比随机梯度下降,也提高了准确度,是迄今为止大家都在用的方法,一般在现在深度学习的不同框架下,提及梯度下降方法,都是默认在指小批量梯度下降方法。
随机梯度下降已被证明了它是一种高效和有效的优化方法,在许多机器学习的成功案例中是核心算法,例如最近的深度学习发展进程,2012年Krizhevsky [12] 、2006年Hinton等 [13] 、2012年的Hinton [14] 等人、2013年的Deng [15] 等人、2014年Graves [16] 等人均在文章中验证了随机梯度下降的有效性。
2.3. 加入动量的随机梯度下降
1964年Poljak提出了经典的动量方法 [6] ,增加了动量矢量v,它积累了历史梯度方向,来代替了真正的梯度。速度是以动量参数 的衰减力度进行更新,若动量参数 越大,则之前的梯度对现在方向的影响也越大。直观的讲,若当前时刻的梯度与历史时刻梯度方向相似,这种趋势会在当前时刻加强,若方向相反,则当前的梯度方向趋势会减弱。
加入动量,会使得在下降初期加速下降,而在越过函数谷面时,学习率会使得两次更新方向基本相反,故而会在原地震荡,此时动量参数会使得更新幅度减小,有助于越过函数谷面。在下降的中后期,函数面的局部极小值所在的吸引盆数量较多,一旦进入吸引盆,则梯度为0,导致前后两次更新方向一致,此时动量参数会使得更新幅度增大,协助跃出吸引盆。
在1983年,Nesterov提出了基于动量变种的加速梯度算法 [17] ,此方法与动量算法的唯一区别就是,计算梯度的不同,Nesterov先用当前的速度v更新一遍参数,在用更新的临时参数计算梯度,相当于添加了矫正因子的动量算法。文章 [17] 指出,在随机梯度下,Nesterov将误差收敛从O (1/k)改进到O (1/k^2),然而在随机梯度下降法下,Nesterov并没有任何改进。作者在文章中提供了经验证据,证明该算法优于梯度下降法、经典动量法和无Hessian-free [8] 算法。
2.4. AdaGrad
在基本的梯度下降法优化中,有一个常见的问题是,要优化的变量对于目标函数的依赖是各不相同的。对于某些变量,已经优化到了极小值附近,但是有的变量仍然在梯度很大的地方,这时候一个统一的全局学习率是可能出现问题的。如果学习率太小,则梯度很大的变量会收敛很慢,如果梯度太大,已经优化差不多的变量就可能会不稳定。
针对这个问题,当时在伯克利加州大学读博士的Jhon Duchi,2011年提出了AdaGrad [7] (Adaptive Gradient),也就是自适应学习率。AdaGrad的基本思想是对每个变量用不同的学习率,设置了全局学习率之后,每次通过,全局学习率逐参数的除以历史梯度平方和的平方根,使得每个参数的学习率不同。这个学习率在一开始会比较大,用于快速梯度下降。随着优化过程的进行,对于已经下降很多的变量,则减缓学习率,对于还没怎么下降的变量,则保持一个较大的学习率。
2.5. RMSProp
AdaGrad的一个值得注意的问题是, 最终会变得非常大,以至于训练速度会慢下来,阻止模型达到局部最小值,RMSProp [18] 是AdaGrad的另一种替代方法,它通过改变梯度累积为指数衰减的移动平均算法,用以丢弃遥远的过去历史,这使得模型能够继续学习。深度神经网络都是在非凸条件下的,RMSProp在非凸条件下结果更好,并在经验上,RMSProp已被证明是有效且实用的深度学习网络优化算法。
Nesterv算法可加速梯度,故而将Nesterv加入到RMSProp [19] ,这样既改变了学习率,Nesterov引入动量又改变了梯度,从两方面对参数进行了更新。
2.6. ADADELTA
2012年,Zeiler提出AdaDelta [20] 算法。它自适应动态学习率,仅使用了一阶信息,并且计算开销也是最小的。该方法不需要对学习速率进行人工调优,而且对于噪声梯度信息、不同的模型体系结构选择、各种数据模式和超参数的选择,都显得很稳健。在分布式集群环境中,使用单机器和大型声音数据集,与其他方法相比,在MNIST数字分类任务上表现了很好的结果。
2.7. ADAM (Adaptive Moment Estimation)
2014年,ADAM [21] 算法被Kingma等人提出,它是moment与RMSProp的结合,Adam 不仅如RMSProp算法那样基于一阶矩均值计算适应性参数学习率,它同时还充分利用了梯度的二阶矩均值(即有偏方差),适合解决含大规模的数据和参数的优化目标,也适合解决包含高噪声或稀疏梯度的问题。具体来说,算法计算了梯度的指数移动均值,超参数 和 控制了这些移动均值的衰减率。 和 的默认参数值接近于1,因此矩估计的偏差接近于0。该偏差通过首先计算带偏差的估计而后计算偏差修正后的估计而得到提升。
Continued
在Adam中,单个权重的更新规则是将其梯度与当前和过去梯度的L2范数成反比例进行缩放调整,Kingma等人 [21] 继而想到了将更新规则泛化到Lp范数的更新规则,将P趋于无穷便得到了Adamax算法。
2.8. Nadam
Nadam (Nesterov-accelerated Adaptive Moment Estimation) [22] 是将Adam与Nesterov加速梯度结合在一起,它对学习率的约束将更强,具备二者的优势,使得此算法在某些问题上的效果更好。
2.9. ANGD
为了加速学习机器的学习动力,减少损失,2018年GH Wei等人 [23] 提出了一种考虑神经结构的几何结构的自然梯度法,并将费雪信息矩阵项加入到修正方程中。在自然梯度法中,其算法规则如下所示:
Continued
3. 学习率衰减
在梯度下降法中,都是给定的统一的学习率,整个优化过程中都以确定的步长进行更新, 在迭代优化的前期中, 较大,则前进的步长就会较长,这时便能以较快的速度进行梯度下降,而在迭代优化的后期,逐步减小 的值,减小步长,这样将有助于算法的收敛,更容易接近最优解。故而如何对学习率的更新成为了研究者的关注点。
在模型优化中,常用到的几种学习率衰减方法有:分段常数衰减、多项式衰减、指数衰减、自然指数衰减、余弦衰减、线性余弦衰减、噪声线性余弦衰减。
学习率衰减所用到的参数,如表1所示。
3.1. 分段常数衰减
这是需要事先定义好的训练次数区间,在对应区间置不同的学习率的常数值,一般情况刚开始的学习率要大一些,之后要越来越小,要根据样本量的大小设置区间的间隔大小,样本量越大,区间间隔要小一点。在真正的网络训练中,需要操作人员根据具体任务对学习率具体设置。图1即为分段常数衰减的学习率变化图,横坐标代表训练次数,纵坐标代表学习率。
Table 1. Parameter description
表1. 参数说明
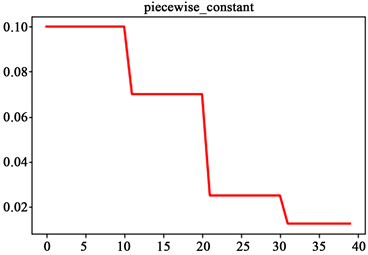
Figure 1. Piecewise constant decay
图1. 分段常数衰减
3.2. 指数衰减
将指数衰减的方式,进行学习率的更新,学习率的大小是和训练次数指数相关的,其更新规则如式(4),这种衰减方式简单直接,收敛速度快,是最常用的学习率衰减方式,如图2示,绿色的为学习率随训练次数的指数衰减方式,红色的即为分段常数衰减,它在一定的训练区间内保持学习率不变。
(4)
3.3. 自然指数衰减
它与指数衰减方式相似,不同的在于它的衰减底数是e,故而其收敛的速度更快,一般用于相对比较容易训练的网络,便于较快的收敛,其更新规则为式(5)。
(5)
如图3所示,为分段常数衰减、指数衰减、自然指数衰减三种方式的对比图,红色的即为分段常数衰减图,阶梯型曲线。蓝色线为指数衰减图,绿色即为自然指数衰减图,很明可以看到自然指数衰减方式下的学习率衰减程度要大于一般指数衰减方式,有助于更快的收敛。
3.4. 多项式衰减
应用多项式衰减的方式进行更新学习率,这里会给定初始学习率和最低学习率取值,然后将会按照给定的衰减方式将学习率从初始值衰减到最低值,其更新规则即为式(6)和式(7)。
这里需要注意的是,有两个机制,降到最低学习率后,到训练结束可以一直使用最低学习率进行更新,另一个是再次将学习率调高,使用decay_steps的倍数,取第一个大于global_steps的结果,也就是式(8).它是用来防止神经网络在训练的后期由于学习率过小而导致的网络一直在某个局部最小值附近震荡,这样可以通过在后期增大学习率跳出局部极小值。
(6)
(7)

Figure 2. Exponential decay
图2. 指数衰减
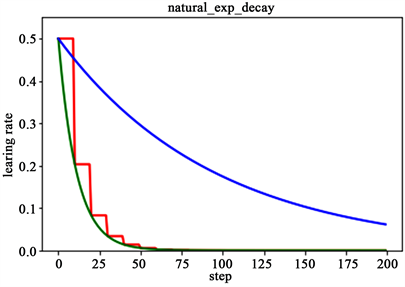
Figure 3. Natural exponential decay contrast diagram
图3. 自然指数衰减对比图
(8)
如图4所示,是多项式衰减图,红色线代表学习率降低至最低后,一直保持学习率不变进行更新,绿色线代表学习率衰减到最低后,又会再次循环往复的升高降低。
3.5. 余弦衰减
就是采用余弦的相关方式进行学习率的衰减 [24] ,衰减图和余弦函数相似。其更新机制即为式(9)-(12)。
(9)
(10)
(11)
(12)

Figure 4. Polynomial decay
图4. 多项式衰减
在此基础上,提出了两个余弦方式衰减的改进方法,分别是线性余弦衰减方式、噪声线性余弦衰减方式。
线性余弦衰减方式,也是基于余弦方式的衰减策略,主要应用于增强学习领域,其更新规则为式(13)-(17).
(13)
(14)
(15)
(16)
(17)
噪声线性余弦衰减方式,是在线性余弦衰减的基础上,加入了噪声。某种程度上增加了学习率寻找最优值的随机性和可能性,其更新方式如式(18)-(22).
(18)
(19)
(20)
(21)
(22)
如图5所示,红色即为标准的余弦衰减曲线,学习率从初始值下降到最低学习率后保持不变。蓝色的线是线性余弦衰减方式曲线,它是学习率从初始学习率以线性的方式下降到最低学习率值。而绿色便是加上噪声的线性余弦衰减方式,是在蓝色曲线的基础上增加了随机噪声。
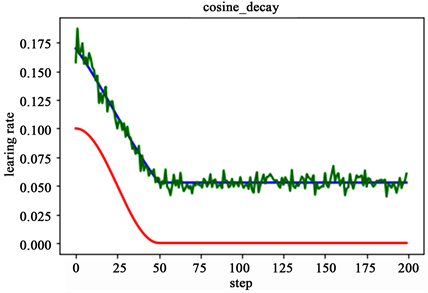
Figure 5. Cosine decay
图5. 余弦式衰减
4. 展望
深度学习越来越重要,不论是超参数的选择,还是优化器的选择,都将是发展深度学习模型的重点,针对现状,提出了对未来优化器的一点思考。
1) 深度学习一般都是基于大量数据下的训练,而且模型一般都是监督学习,在训练前期,需要大量的人力去标注样本,如何节省前期的训练成本也是现在需要考虑的问题。
2) 基于优化器方法的梳理,如何加快收敛速度、减少搜索中的震荡仍是下一步研究中需要考虑的问题。牛顿法是经典的方法,但是由于二阶导数(Hessian矩阵)在大数据量的样本下,计算开销很大,可以尝试协方差的方向来考虑这个问题,是一个新的研究点。
随着深度学习的发展,未来将会有更多的人参与进来,所存在的问题也将能够被更好地解决,而深度学习技术也将会越来越成熟,同时也会为我们的生活带来更多的便利。
基金项目
国家自然科学基金(11101012)。
文章引用
冯宇旭,李裕梅. 深度学习优化器方法及学习率衰减方式综述
An Overview of Deep Learning Optimization Methods and Learning Rate Attenuation Methods[J]. 数据挖掘, 2018, 08(04): 186-200. https://doi.org/10.12677/HJDM.2018.84020
参考文献
- 1. Hochreiter, S. and Schmidhuber, J. (1997) Long Short-Term Memory. Neural Computation, 9, 1735-1780. |https://doi.org/10.1162/neco.1997.9.8.1735
- 2. Socher, R., Lin, C.C., Ng, A.Y. and Manning, C. (2011) Parsing Natural Scenes and Natural Language with Recursive Neural Networks. Proceedings of the 28th International Confer-ence on Machine Learning (ICML-11), Bellevue, WA, 28 June-2 July 2011, 129-136.
- 3. Glorot, X., Bordes, A. and Bengio, Y. (2012) Deep Sparse Rectifier Neural Networks. International Conference on Artificial Intelligence and Sta-tistics, 15, 315-323.
- 4. Le, Q.V., Jaitly, N. and Hinton, G.E. (2015) A Simple Way to Initialize Recurrent Networks of Rectified Linear Units. Computer Science.
- 5. Talathi, S.S. and Vartak, A. (2015) Improving Performance of Re-current Neural Network with Relu Nonlinearity. Computer Science.
- 6. Poljak, B.T. (1964) Some Methods of Speeding up the Convergence of Iterative Methods. USSR Computational Mathematics & Mathematical Physics, 4, 1-17. https://doi.org/10.1016/0041-5553(64)90137-5
- 7. Duchi, J., Hazan, E. and Singer, Y. (2011) Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. Journal of Machine Learning Research, 12, 257-269.
- 8. Martens, J. (2010) Deep Learning via Hessian-Free Optimization. International Conference on Machine Learning, Haifa, Israel, 21-24 June 2010, 735-742.
- 9. Nesterov, Y. (2004) Introductory Lectures on Convex Opti-mization. Applied Optimization, 87, xviii, 236.
- 10. Meng, X., Bradley, J., Yavuz, B., et al. (2015) MLlib: Machine Learning in Apache Spark. Journal of Machine Learning Research, 17, 1235-1241.
- 11. Robbins, H. and Monro, S. (1951) A Stochastic Approximation Method. Annals of Mathematical Statistics, 22, 400-407. https://doi.org/10.1214/aoms/1177729586
- 12. Hinton, G.E. and Salakhutdinov, R.R. (2006) Reducing the Di-mensionality of Data with Neural Networks. Science, 313, 504-507. https://doi.org/10.1126/science.1127647
- 13. Hinton, G., Deng, L., Yu, D., et al. (2012) Deep Neural Networks for Acoustic Modeling in Speech Recognition: The Shared Views of Four Research Groups. IEEE Signal Processing Magazine, 29, 82-97. https://doi.org/10.1109/MSP.2012.2205597
- 14. Krizhevsky, A., Sutskever, I. and Hinton, G.E. (2012) ImageNet Classification with Deep Convolutional Neural Networks. International Conference on Neural Information Processing Systems, 60, 1097-1105.
- 15. Deng, L., Li, J., Huang, J.T., et al. (2013) Recent Advances in Deep Learning for Speech Research at Microsoft. IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, 26-31 May 2013, 8604-8608.
- 16. Graves, A. (2014) Generating Sequences with Recurrent Neural Networks.
- 17. Nesterov, Y. (1983) A Method of Solving a Convex Programming Problem with Convergence Rate O(1/K2). Soviet Mathematics Doklady, 27, 372-376.
- 18. Tieleman, T. and Hinton, G. (2012) Lecture 6.5—RMSProp, COURSERA: Neural Networks for Machine Learning. Technical Report.
- 19. Graves, A., Mohamed, A.R. and Hinton, G. (2013) Speech Recognition with Deep Recurrent Neural Networks. IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, 26-30 May 2013, 6645-6649.
- 20. Zeiler, M.D. (2012) ADADELTA: An Adaptive Learning Rate Method.
- 21. Kingma, D. and Ba, J. (2014) Adam: A Method for Stochastic Optimiza-tion.
- 22. Timothy, D. (2016) Incorporating Nesterov Momentum into Adam.
- 23. Wei, W.G.H., Liu, T., Song, A., et al. (2018) An Adaptive Natural Gradient Method with Adaptive Step Size in Multilayer Perceptrons. Chinese Auto-mation Congress, 1593-1597.
- 24. Loshchilov, I. and Hutter, F. (2016) SGDR: Stochastic Gradient Descent with Warm Restarts.
