Mechanical Engineering and Technology
Vol.07 No.02(2018), Article ID:24481,7
pages
10.12677/MET.2018.72013
Study on the Influence Rules of Planetary Gear Eccentric Errors on Dynamic Load Sharing Behavior of a Planetary Gear Train
Shangzhen Sun1, Aimin Yao1, Tongjie Li2*, Jie Ma2, Juan Wang2
1Bengbu Planet Engineering Machinery Co. Ltd, Bengbu Anhui
2College of Mechanical Engineering, Anhui Science & Technology University, Chuzhou Anhui

Received: Mar. 27th, 2018; accepted: Apr. 17th, 2018; published: Apr. 24th, 2018

ABSTRACT
By using the method of numerical simulation, the influence rules of planetary gear eccentric errors on dynamic load sharing behavior of a planetary gear train are studied based on a nonlinear lateral-torsional vibration model. Under the assumption that all of the planetary gears have the same eccentric errors, planetary gear train has a threshold value error; the dynamic load sharing behavior of the system will remain unchanged with the eccentric error of planetary gears changing under the threshold value error; the dynamic load sharing behavior of the system will worsen significantly with the eccentric error of planetary gears increase above the threshold value error.
Keywords:Planetary Gear Train, Nonlinear Lateral-Torsional Vibration Model, Planetary Gear Eccentric Errors, Dynamic Load Sharing Behavior
行星轮偏心误差对行星齿轮传动系统均载性能的影响
孙尚贞1,姚爱民1,李同杰2*,马杰2,王娟2
1蚌埠市行星工程机械有限公司,安徽 蚌埠
2安徽科技学院机械工程学院,安徽 滁州

收稿日期:2018年3月27日;录用日期:2018年4月17日;发布日期:2018年4月24日

摘 要
本文基于行星齿轮传动系统弯扭耦合非线性动力学模型,采用数值仿真的手段,研究了行星轮偏心误差对行星齿轮传动系统均载性能的影响规律。研究结果发现,在各行星轮偏心量一致的条件下,行星齿轮传动系统的行星轮偏心量存在一个误差阀值,当偏心量在小于该阀值的区间内变化时,行星齿轮传动系统的均载性能没有明显变化;当偏心量在大于该阀值的区间内增大时,行星齿轮传动系统的均载性能会显著降低。
关键词 :行星齿轮系,弯扭耦合非线性动力学模型,行星轮偏心,均载性能

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
行星轮间载荷分布均匀是指输入的太阳轮传递给各行星轮的啮合作用力的大小相等。在没有采取任何均载措施的情况下,实际上行星轮间的载荷分布是不均匀的;即使采取了某种均载机构,由于制造和安装误差的影响,在行星齿轮传动工作的过程中,行星轮间的载荷分布也并非完全是分配不均匀,因而引起局部载荷增大、产生振动、降低了效率,造成某些零部件的过早损坏。这样,行星齿轮机构传动的优点就得不到充分发挥。
因此,提高载荷在各行星轮上的分配均匀性是行星轮系中要解决的一个重要问题。深入研究其均载特性,既具有重要的理论意义,也具有重大的实际应用价值。对于延长工作寿命、降低振动和噪声以及保证其工作可靠性等方面都具有重要理论意义和实际应用价值。国内有关学者也对这一重要课题展开了一系列的研究 [1] - [6] ,但是均没有给出行星轮偏心误差值对系统均在性能的影响规律曲线。
本文将基于行星齿轮传动系统的弯扭耦合非线性动力学模型,通过直接数值积分方法,在各行星轮偏心误差一致的情况下,研究行星轮偏心误差对行星齿轮传动系统的动态均载性能的影响规律。
2. 动力学模型
本文动力学模型采用在文献 [6] 中经典的行星齿轮传动系统弯扭耦合非线性振动模型,同时增加考虑各种误差的传递关系,以下是该模型的简单介绍。
图1是行星齿轮传动系统的弯扭耦合非线性动力学模型。2K-H型行星齿轮传动系统的运动简图,由太阳轮、内齿圈、行星架和N个行星轮组成。系统输入功率Pin经太阳轮分流给N个行星轮,又汇流至行星架输出功率Pout。图1是系统扭转非线性动力学模型,太阳轮以S表示,第i个行星齿轮以pi表示,行星架以C表示,内齿圈以R表示,并固定于基础之上,各齿轮均为直齿圆柱齿轮。
模型中除了扭转振动中太阳轮、行星架、第i个行星轮的角位移 、
、
外,还考虑了太阳轮轴横向和纵向两个弯曲振动位移,分别以
和
来表示。模型中其他符号的物理意义:太阳轮、第i个行星轮、内齿圈的基圆半径分别以
、
、
表示;行星架半径以
表示,其值为太阳轮与行星轮的节圆半径之和,标准安装下亦即太阳轮与行星轮的分度圆半径之和;太阳轮与第i路行星轮组成的外啮合
、
、
外,还考虑了太阳轮轴横向和纵向两个弯曲振动位移,分别以
和
来表示。模型中其他符号的物理意义:太阳轮、第i个行星轮、内齿圈的基圆半径分别以
、
、
表示;行星架半径以
表示,其值为太阳轮与行星轮的节圆半径之和,标准安装下亦即太阳轮与行星轮的分度圆半径之和;太阳轮与第i路行星轮组成的外啮合

Figure 1. Bending-torsional coupling nonlinear dynamic model of planetary gear train
图1. 行星齿轮传动系统弯扭耦合非线性动力学模型
副的啮合刚度、啮合阻尼系数、半齿侧间隙、综合啮合误差分别以 、 、 、 表示;内齿圈与第i路行星轮组成的内啮合副的啮合刚度、啮合阻尼系数、半齿侧间隙、综合啮合误差分别以 、 、 、 表示。图中太阳轮、行星轮以及内齿圈的齿数分别以 、 、 表示。
模型中的综合啮合误差同时考虑了各齿轮副静传递误差和各齿轮的偏心误差。各齿轮偏心误差相对齿轮副啮合线方向的投影关系如图2所示。图中,
为太阳轮偏心误差, 为内齿圈偏心误差,
为行星轮偏心误差,a为渐开线齿轮的啮合角,
为太阳轮的偏心误差与第i路外啮合线方向的夹角,
为第i个行星轮偏心误差与第i路外啮合线方向的夹角,
为第i个行星轮偏心误差与第i路内啮合线方向的夹角,
为内齿圈偏心误差与第i路内啮合线方向垂线的夹角,
为太阳轮偏心误差与Hs轴之夹角,
为第i个行星轮偏心误差与xpi轴之夹角,
为内齿圈偏心误差与Hs轴之夹角。Hs-Vs坐标系以行星架的中心为坐标原点,坐标轴固结在行星架上,Hs轴穿过第1个行星轮的轮心;xpi-ypi坐标系以第i个行星齿轮中心为坐标原点,坐标轴固结在i个行星轮上。在此动坐标系下第i个行星轮相对于Hs轴之夹角恒为
。
为内齿圈偏心误差,
为行星轮偏心误差,a为渐开线齿轮的啮合角,
为太阳轮的偏心误差与第i路外啮合线方向的夹角,
为第i个行星轮偏心误差与第i路外啮合线方向的夹角,
为第i个行星轮偏心误差与第i路内啮合线方向的夹角,
为内齿圈偏心误差与第i路内啮合线方向垂线的夹角,
为太阳轮偏心误差与Hs轴之夹角,
为第i个行星轮偏心误差与xpi轴之夹角,
为内齿圈偏心误差与Hs轴之夹角。Hs-Vs坐标系以行星架的中心为坐标原点,坐标轴固结在行星架上,Hs轴穿过第1个行星轮的轮心;xpi-ypi坐标系以第i个行星齿轮中心为坐标原点,坐标轴固结在i个行星轮上。在此动坐标系下第i个行星轮相对于Hs轴之夹角恒为
。
行星齿轮传动系统中各齿轮副啮合线上的综合误差激励为
, (1)
式中, 、 分别为第i外、内啮合副静传递误差幅值路, , , , 为太阳轮转速, 为行星架转速, 为行星轮转速, 为太阳轮偏心误差变化的初相位, 为第i个行星轮偏心误差变化的初相位, 为内齿圈偏心误差变化的初相位。
那么,行星齿轮传动系统无量纲化的弯扭耦合(4+N)自由度非线性运动微分方程为
 (a) 偏心误差与外啮合线的投影关系 (b) 偏心误差与内啮合线的投影关系
(a) 偏心误差与外啮合线的投影关系 (b) 偏心误差与内啮合线的投影关系
Figure 2. Geometrical relationship of eccentricity error in gear pair
图2. 系统各偏心误差与啮合线的投影关系
 (2)
(2)
式中,
、
、
分别表示太阳轮、第i行星轮、行星架角位移在其啮合点相对位移的贡献量,字母上加“-”表示相应物理量的量纲一量,加“‥”表示加速度,加“﹒”表示速度;t为量纲以时间;
为固有频率;
为太阳轮质量;
、
、
分别为太阳轮、第i行星轮、行星架的当量质量;
、
分别为第i外、内啮合副的齿侧间隙,
为标称尺度;
、 分别为系统功率输入、输出断的当量载荷;f为间隙非线性函数;
、
分别为第i外、内啮合副啮合点的相对位移,其表达式为
分别为系统功率输入、输出断的当量载荷;f为间隙非线性函数;
、
分别为第i外、内啮合副啮合点的相对位移,其表达式为
(3)
各内外齿轮副的动载荷为
(4)
以上动力学模型中涉及到的相关物理量的具体表达式请参看文献 [6] 。
3. 均载性能的考评
t时刻系统的第i个行星齿轮分配的载荷与该时刻N个行星轮的平均载荷的比值即为该时刻该行星轮的动态均载系数,其外内啮合副各行星轮的动态均载系数分别以 和 表示
(5)
显然, 越接近1,表示该时刻外啮合副上各路行星齿轮承担的动载荷越均匀; 越接近1,表示该时刻内啮合副上各路行星齿轮承担的动载荷越均匀。 在一个系统周期内随时间的变化情况就刻画了行星齿轮外啮合副各行星齿轮的均载性能; 在一个系统周期内随时间的变化情况就刻画了行星齿轮内啮合副各行星齿轮的均载性能。
行星齿轮传动系统的外内啮合副在t时刻的动态均载系数定义为该时刻所有N路啮合副上行星齿轮动态均载系数的最大值与平均值之比
(6)
按照定义(6),在正常啮合状态下,行星齿轮传动系统的内外啮合副的动态均载系数 与 均是大于1的数值。由于系统动态均载系数 与 反映的是行星齿轮传动系统的内外啮合副中偏载程度最大的传动副的均载系数,因而能够更加简单有效的反映整个系统的均载性能,所以本章以下数值仿真中,大多模拟的是行星齿轮传动系统的动态均载系数 与 的变化曲线。
内外啮合副的均载系数 与 定义为系统动态均载系数 与 在一个系统周期T内波动的最大值
(7)
式中,系统周期T为行星齿轮系统的静传递误差变化周期、太阳轮偏心误差变化周期、行星轮偏心误差变化周期以及内齿圈偏心误差变化周期的公倍数。
行星齿轮传动系统的均载性能也可以依据内外啮合副的均载系数 与
来考评,显然均载系数值越接近1,说明系统的均载性能越好。
与
来考评,显然均载系数值越接近1,说明系统的均载性能越好。
4. 行星轮偏心误对均载性能的影响规律
以下基于弯扭耦合非线性动力学模型(1),通过直接数值积分方法,研究行星轮偏心误差对行星齿轮传动系统的均载性能的影响规律。系统基本参数为:模数 , , , , , , , ,太阳轮转速 ,太阳轮轴弯曲刚度 , 。
在各行星轮偏心误差一致的条件下,考查行星轮偏心误差值对系统均载性能的影响规律。固定Es=1×10
图形5、6显示:当行星轮偏心误差Epi值小于5 um时,系统内外啮合副的均载系数随行星轮偏心量的变化曲线近似为一条水平线,说明行星轮偏心误差Epi值较小时,系统的均载性能对Epi的变化不敏感;

Figure 3. Load sharing coefficient of every external gear pair when Epi = 1 × 10−6 m
图3. Epi = 1 × 10−6 m时外啮合副动态均载系数

Figure 4. Load sharing coefficient of every internal gear pair when Epi = 1 × 10−6 m
图4. Epi = 1 × 10−6 m时内啮合副动态均载系数
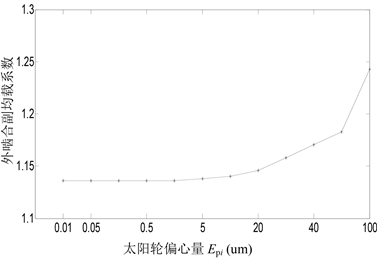
Figure 5. Load sharing coefficient of external gear pair with the eccentricity
图5. 外啮合副均载系数随行星轮偏心量的变化曲线
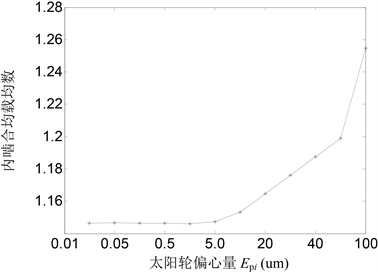
Figure 6. Load sharing coefficient of internal gear pair with the eccentricity
图6. 内啮合副均载系数随行星轮偏心量的变化曲线
当行星轮偏心误差Epi值大于5 um时,系统内外啮合副的均载系数随行星轮偏心量的增大而显著增大,说明行星轮偏心误差Epi值较大时,系统的均载性能会随者Epi的增大而显著降低。
5. 结论
总结以上仿真可以获得如下规律:
1) 存在一个行星轮偏心误差阀值,当Epi小于该阀值时,Epi的变化对行星齿轮传动系统的均载性能没有明显的影响;当Epi大于该阀值时,Epi的增大会显著削弱行星齿轮传动系统的均载性能。
2) 机械设计时,要注意通过控制齿轮精度的手段使行星轮偏心误差处于该误差阀值之下以保证行星齿轮传动系统的均载性能。误差阀值可以通过大量的数值试验获得。
基金项目
机械传动国家重点实验室开放课题(SKLMT-KFKT-201703);安徽科技学院自然科学一般项目(ZRC 2016488);蚌埠市行星工程机械有限公司委托横向课题(直连式垂直循环停车库专用减速机提效降噪方案研究)。
文章引用
孙尚贞,姚爱民,李同杰,马杰,王娟. 行星轮偏心误差对行星齿轮传动系统均载性能的影响
Study on the Influence Rules of Planetary Gear Eccentric Errors on Dynamic Load Sharing Behavior of a Planetary Gear Train[J]. 机械工程与技术, 2018, 07(02): 105-111. https://doi.org/10.12677/MET.2018.72013
参考文献
- 1. 叶福民, 朱如鹏, 鲍和云, 等. 非等模数非等压力角行星齿轮系的动力学均载特性[J]. 华南理工大学学报, 2011, 39(1): 117-123.
- 2. 方宗德, 沈允文, 黄镇东. 2K-H行星减速器的动态特性[J]. 西北工业大学学报, 1990, 10(4): 361-371.
- 3. 陆俊华, 朱如鹏, 靳广虎. 行星传动动态均载特性分析[J]. 机械工程学报, 2009, 45(5): 85-90.
- 4. 朱增宝, 朱如鹏, 李应生, 等. 安装误差对封闭差动人字齿轮传动系统动态均载特性的影响[J]. 机械工程学报, 2012, 48(3): 16-24.
- 5. 周建星, 董海军. 基于非线性动力学的行星传动均载性能研究[J]. 机械科学与技术, 2008, 27(6): 808-811
- 6. 李同杰, 朱如鹏, 鲍和云, 等. 行星齿轮系扭转非线性振动建模与运动分岔特性研究[J]. 机械工程学报, 2011, 47(21): 76-83.