Mechanical Engineering and Technology
Vol.
08
No.
05
(
2019
), Article ID:
32491
,
11
pages
10.12677/MET.2019.85041
Review on 3D Mesh Model Analysis Based on the Discrete Differential Geometry
Dong-Qing Wu1,2, Jian Gao1*, Zheng-Tao Xiao1,3
1State Key Laboratory of Precision Electronic Manufacturing Technology & Equipment, Guangdong University of Technology, Guangzhou, Guangdong
2School of Computational Science, Zhongkai University of Agriculture and Engineering, Guangzhou, Guangdong
3School of Electro-mechnical Engineering, Guangdong Polytechnic of Industry and Commerce, Guangzhou, Guangdong

Received: Sep. 19th, 2019; accepted: Oct. 4th, 2019; published: Oct. 11th, 2019

ABSTRACT
The analysis of 3D models has become a hot topic in computer graphics research in recent years. Aiming at the application problems of mesh denoising and smoothing, mesh parameterization and non-rigid registration in the field of discrete differential geometry, this paper reviews the literature on the application of discrete differential geometry theory in analysis, mathematical modeling and algorithm design in recent years, and introduces the research progress of discrete differential geometry in the field of 3D model analysis. The difficulties and possible research directions in the future are summarized.
Keywords:3D Model Analysis, Discrete Differential Geometry, Mesh Smoothness, Mesh Parameterization, Non-Rigid Registration
基于离散微分几何的3D网格模型分析进展综述
吴东庆1,2,高 健1*,肖正涛1,3
1精密电子制造技术与装备省部共建国家重点实验室广东工业大学机电工程学院,广东 广州
2仲恺农业工程学院计算科学学院,广东 广州
3广东工贸职业技术学院机电学院,广东 广州

收稿日期:2019年9月19日;录用日期:2019年10月4日;发布日期:2019年10月11日

摘 要
3D网格模型的分析越来越成为近年来计算机图形学研究的热点问题。文中针对3D网格模型分析领域内的网格去噪平滑、网格参数化以及非刚性配准等应用问题,评述和回顾近年来应用离散微分几何理论进行分析、数学建模和算法设计的文献,介绍离散微分几何在3D模型分析领域的研究进展,并对相关问题难点和未来可能的研究方向进行了归纳和总结。
关键词 :3D网格模型分析,离散微分几何,网格光滑,网格参数化,非刚性配准

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
长久以来,3D网格模型分析是数字制造、逆向工程、医学、生物研究以及动画工业领域中广泛存在的难点问题。在微分几何中,可以将3D模型视为一个嵌入 的二维流形,并根据流形在空间里内蕴的信息来研究分析3D模型,进而推导相关算法 [1] 。这种基于流形的抽象,使研究者更容易发现和把握3D模型的内在规律性。3D模型的采集都是采用离散化的方式进行,因此基于面网格、体网格的描述是3D模型在计算机里表达的主流形式。微分几何里的各种算子,从本质上刻画了网格顶点与邻接顶点、网格面片与邻接面片的差异值与差异变化率,整体或者局部的几何、拓扑性质。这些算子既有内蕴也有外蕴的,并且具有与坐标系、大小和比例无关的性质,非常适合用于对3D模型进行整体或者局部分析的研究。
微积分中的一阶导数(偏导)、二阶导数(偏导)对于分析曲线、曲面形状,包括极大极小值,拐点、拟合、插值以及样条等问题等起到至关重要的作用。微积分的诞生是和欧氏空间里的曲线、曲面研究紧密相连的,但随着更一般的空间——流形的发现,欧拉(L. Euler)、蒙日(G. Monge)、嘉当(Élie J. Cartan)和黎曼(G. F. B. Riemann)等人将微积分推广到流形上。他们运用数学分析的理论在无穷细分的范围内略去高阶无限小,从而将一些复杂的非线性的函数关系变为线性的,由此衍生出流形上的一系列离散微分算子,在3D模型研究中发挥着基础性的作用 [2] [3] [4] 。在机器学习炙手可热的今天,很多研究者力图从微分几何算子的特征值以及特征函数(Eigenfunction)的角度来提取3D模型的内蕴信息,从而提升深度学习神经网络的训练速度以及和网络泛化能力 [5] [6] [7] [8] 。
2. 离散微分几何的理论框架
微分几何中的许多重要概念可以借助外微分形式(Differential form)来简洁地表示。例如在网格中的点,在外微分里被称为0-形式,线段为1-形式,面片为2-形式,以及基于Stockes定理,将外微分与积分完美地联系起来 [9] 。3D模型中引入离散微分几何理论表示为很多问题的解决提供了崭新的视角,与其他方法相比,该方法是建立在坚实的数学基础上,在一些问题的求解中,可以得到问题的闭式解(closed-form solution),并在全局上保证解的收敛性和稳定性,得到的结论及其应用效果在不计其数的场景下得到充分验证。离散微分几何涉及了一系列的概念和算子,下面简要介绍相关术语及其数学定义。
2.1. 基本概念
网格:是连续3D模型的离散形式,任何一个网格都可以用三元组来表示为 ,其中的V是点集 , 表示点的个数,每个 对应着 中的一个顶点;其中的E为边子集 ;F是面子集 。
退化网格:在 中出现有重合的点,线、面的情况,即 (重合点)或者 的两对端点重合,或者 的两组端点重合的情况,将严重影响网格上微分算子的计算精度。一般情况下都要删除或者合并重合的顶点、边或面。
场:现实系统中温度、压力、密度、速度等物理量在空间内的分布状态,而在 中任一个坐标分量也可以视为场。
网格上的标量场:在 上任意一点,如果存在标量函数 满足 。为了便于微分
计算,常常用分段线性基函数族 对 进行分解,并表示为 。其中 满足当j恰好
落在 时 ,在其他地方 。而v的三个坐标 正好就是三个标量场,当然也可以拓展为温度,密度等物理量。
网格上的矢量场:在 上如果存在矢量函数 ,满足在任一三角面片 内部取值都是常值矢量 ,则称 为定义在 上的矢量场。
2.2. 算子
网格上的微分算子:3D分析中为了把握形状的特征,发现其内在本质,常常会用到定义在网格上的微分算子。具体包括有梯度算子 、散度算子 和旋度算子 以及拉普拉斯算子 。
梯度算子 :在 上任意一个三角片f内一点v的梯度定义为
(1)
上式中的 处基函数的梯度为一个在f上的向量 , 为f的面积, 表示为 的
对边 逆时针旋转90度方向。梯度在几何上表示为f在边 上的高。
散度算子 :作用于矢量 的算子,定义为:
(2)
其中 表示以 为顶点的三角面片集合, 表示 的面积, 表示 内的矢量, 表示 处的基函数在 的梯度。
拉普拉斯算子 :是作用于标量场 的二阶微分算子,定义为梯度的散度:
(3)
其中
表示以
为中心一阶邻域的顶点集合的下标,(3)中权重
的选取有如下四个方面的要求:(1) 对称性条件
;(2) iff
时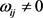 ;(3) 归一化条件
;(4) 非负条件
,都有
。在满足上述条件下,根据不同的问题
可以采用多种形式。例如 [10] 采用余切形式
,
分别表示边
;(3) 归一化条件
;(4) 非负条件
,都有
。在满足上述条件下,根据不同的问题
可以采用多种形式。例如 [10] 采用余切形式
,
分别表示边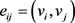 在相邻两个三角形的对角。该算子的几何意义是描述空间顶点与邻域顶点的函数值的均值差异。基于该算子,可以求出平均曲率
。很多物理规律如泊松方程、波动方程、Navier-Stokes方程等,都以拉普拉斯算子来表示的。该算子推广到黎曼流形上被称为Laplace-Beltrami算子(LBO)。基于LBO设计的各种三角网格算法已经得到的广泛的应用。例如:
在相邻两个三角形的对角。该算子的几何意义是描述空间顶点与邻域顶点的函数值的均值差异。基于该算子,可以求出平均曲率
。很多物理规律如泊松方程、波动方程、Navier-Stokes方程等,都以拉普拉斯算子来表示的。该算子推广到黎曼流形上被称为Laplace-Beltrami算子(LBO)。基于LBO设计的各种三角网格算法已经得到的广泛的应用。例如:
热传导方法:温度场随着时间变化的物理方程是热传导方程,也可以视为拉普拉斯算子的泛函推广。如 表示曲面上某一点x在t时刻的温度分布函数,则热传导方程为:
(4)
方程的解为 ,y是对x有影响的顶点, 作为热核的含义是指它表示
了x受y的影响程度。对 进行特征分解得到:
(5)
其中 分别为 算子作用于标量场后对应的矩阵的第i个特征值和特征向量。基于热传导方法的各向异性热核方法,可以应用在网格修复、网格切割、测地线计算、多尺度特征提取领域 [11] 。
3. 基于离散微分几何的3D模型分析
自上个世纪九十年代以来,3D模型分析领域的热点问题包括:3D形状的参数化、纹理计算、去噪光滑、聚类分析、配准、自动识别以及差异评价等等。围绕这些分析问题,出现了大量的基于离散微分几何基础理论的实用算法。由此,很多基于全局或者局部最优化的复杂非线性计算过程都可以统一到离散微分理论框架下来。本文选取最典型的三个问题,即网格去噪光滑、网格参数化以及非刚性配准问题来展开评述。
3.1. 网格去噪光滑
有限元模拟分析中的关键问题是求解连续性方程、动量方程以及能量方程问题,求解的精度和收敛性受到网格生成质量的极大影响。随着研究涉及的形状及其边界条件越来越复杂,围绕3D模型的去噪光滑过程中,保持网格模型特征的优化问题,吸引了越来越多研究者的关注。
网格数据(包括顶点的坐标本身)可以视为一种分布在曲面上的信号,一般来说,尖锐特征和噪声属于高频分量。而很多特征信息和噪声无论是直观上或是本质上是模棱两可的,因此,处理好去噪和保持特征二者之间的平衡,是一个棘手的问题。最早出现的拉普拉斯光顺法通过计算每个顶点的拉普拉斯坐标,然后按照一定的规则移动顶点,使得网格的分布更为均衡,但往往会导致网格萎缩进而体积变小的问题 [12] 。文献 [13] 将曲面坐标视为信号输入,将离散傅里叶分析理论应用于离散曲面的网格光顺问题。Taubin等人首先将原始信号变换到Laplace算子的特征向量空间,然后过滤掉高频部分(噪音),保留低频部分(形状),从而实现网格光顺的目的。具体方法是首先将(3)写为如下矩阵形式:
(6)
其中
为(3)中的标量函数
的离散形式,为一个
维的列向量,
作用于
相当于
左乘对称矩阵
。
中的元素
,只有当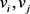 恰好有邻接关系,才不等于零。
是一个实对称矩阵,因此是半正定的,进而可求出其特征值与特征向量为
和
。之后设计低频的过滤器
迭代N次来过滤原始信号
中不需要的部分。
恰好有邻接关系,才不等于零。
是一个实对称矩阵,因此是半正定的,进而可求出其特征值与特征向量为
和
。之后设计低频的过滤器
迭代N次来过滤原始信号
中不需要的部分。
(7)
针对传统高斯过滤器存在褶皱的问题,Taubin定义了新的滤波器 ,其中引入了新的阻尼因子 ,达到在过滤频率接近 的信号的同时进行补偿,避免了褶皱的问题。
文献 [10] 在Taubin研究的基础上,将频谱过滤方法扩展到非正则网格,并基于共轭梯度求解器来解决数值计算的稳定性问题。文献 [14] 针对过度平滑化的问题,提出一种将网格法线非线性扩散的综合评价方法,来达到保持网格原有外形特征的目的。文献 [15] 提出了一个分两阶段去噪平滑网格数据的方法,并在第二阶段采用了基于边权值的Laplace算子来计算其微分坐标的算法。上述算法属于各向同性扩散类的平滑算法,相关的研究包括 [16] [17] [18] [19] 。
针对各向同性算法容易造成特征丢失的问题,近年来的研究主要集中于各项异性的算法。例如通过法向与坐标结合的方法 [20] ,还有基于自适应尺度特征来增强信号的平滑各向异性滤波器 [21] 。近5年来,比较流行的方法是用数值方法求解平滑网格的扩散方程方法(diffusion equation) [22] 。然而,这些方法使用的离散格式往往会受到数值不稳定性和不精确性的影响。在有限元分析中,网格的质量对分析效果起到很大的作用,研究高效率、鲁棒而且能保持曲面完整性以及连续性好的网格优化算法是很多研究者的追求目标。文献 [23] 基于Laplace-Beltrami eigenfunctions提出了一个曲面平滑框架,具体是通过研究Green函数各向同性传导方程中包括有Laplace-Beltrami算子的线性组合的特点,得到其展开形式进而达到构造热核(heat kernel)平滑的目的。Wei等人 [24] 针对形体本身的相似性,将网格去噪问题转换为一个低秩矩阵的修复问题,提出了一个分片分层的噪声过滤方法。Liao [25] 等人引入二阶Laplace算子以及推广了Giaquinta–Hildebrandt算子,进而求出算子的特征函数(eigenfunction),用于捕捉曲面的凹凸特征,并应用于网格平滑处理。
文献 [26] [27] 针对非凸网格和非平面网格上LBO的构造方法问题,从黎曼流形度量出发,给出了任意多边形网格上离散LBO的构造方法。文献 [28] 将半离散LBO定义为四边形网格上离散LBO的极限,并证明了该网格收敛于半离散曲面。
总体看来,既往文献都取得不错的去噪平滑效果,但由于不同场景对于形状特征的定义和程度不尽相同,因此没有任何一个方法能够对所有类型的噪声有效。离散LBO算子在平滑算法中起到基础性作用,目前的研究热点主要是围绕如何构造收敛性更好、能保持原有模型尖锐特征而且适应性更强的权重矩阵的目标来开展。目前看来,围绕多边形网格以及非平面网格的热传导方程Heat kernel方法以及是近年来的研究热点。
3.2. 网格参数化
很多在复杂网格上直接执行的优化运算或者统计计算,往往存在计算量大而精度不稳定的问题。但如果能转换到简单的参数域上执行,将有效地提升计算的精度和效率。网格曲面参数化就是将3D曲面网格 与平面参数域 之间建立一一映射 。
网格参数化在生产实践中具体的应用包括制造业中的加工排料、刀具路径设计以及真实感纹理坐标生成等问题,另外在虚拟肠镜、脑皮层CT等问题也有广泛的应用 [29] 。根据问题背景的不同,网格参数化方法可分为四大类:均匀参数化映射、保角映射、保面积映射以及保特征映射。无论是哪种参数化方法,都要求参数域上的网格与前面上的网格在拓扑上是同构的,而且要确保某种意义下几何量的差异最小化。我们主要讨论应用了基于离散微分几何理论的Dirichlet能量和Circle packing参数化方法,这两种方法也是近年来比较热门的方法。这些方法都是基于能量最小化的思路来设计的,即根据问题域需要定义出合理的变形能 。
(1) Dirichlet能量方法的网格参数化
文献 [30] 讨论了网格是满足闵可夫斯基泛函条件(旋转平移不变性、连续性、可加性)的几个内蕴几何量:面积、欧拉示性数(Eulogy)以及边界周长,提出了给定顶点的一环邻接三角面片的变形能量的定义:
(8)
其中 为待定常数, 为面积的变形能量定义为Dirichlet能量,其可能的最小值满足面积
.
(9)
为欧拉示性数的变形能量,定义为:
(10)
其中符号的含义如图1所示。

Figure 1. A ring on a mesh mapped to a ring on a plane domain
图1. 网格上的一环映射到平面域上的一环
为了求出使得 取得极小值的 ,可以分别求出偏导为零的点来讨论,即存在(11)成立。
(11)
可以看出,(11)就是前文中的 作用于平面域U上坐标值在 上的标量场。
同理也可以给出求 驻点的等式:
(12)
综上,将(11),(12)以及边界条件(可以是固定边界或者是Neumann边界)的约束联立线性方程组,就可以求出U上对应的 。
(2) Circle packing的网格参数化
Thurston首先提出了用一系列变化的圆来近似从平面到单位圆盘的黎曼映射,从而实现网格到平面的保角映射 [31] 。文献 [32] 提出一种新的构造任意拓扑面网格到平面的离散共形映射的方法。该方法是基于圆模式(Circle packing),即每个三角面与一个圆相对应,按照预设的夹角来调整圆的半径来达到保角映射的目的。该方法相对于调和映射有两方面的优势:1) 支持自然边界条件和规定的曲率控制边界形状的边界;2) 该解是基于作为函数的凸能量,用简单的显式表达式表示对数半径变量梯度和Hessian矩阵,因而更为稳健和高效。
顾险峰等人 [33] 研究具有circle packing度量的网格,思路是先计算每个顶点的高斯曲率 和预设高斯曲率 后,找到一个新的circle packing度量 ,即新的圆心及其半径的集合,使其诱导的曲率等于设定的高斯曲率,定义离散Ricci流方程为:
(13)
其中 是 处圆的半径。令 代入(13),两边积分可以得到如下积分方程。
(14)
上述方法仅适用于圆盘拓扑结构的网格,对于更复杂的拓扑结构,需要多次分割环柄至模型的拓扑变为圆盘拓扑,才能做后续的Circle packing。
综合近年来的相关文献,可以看出网格参数化主要存在如下难点问题:一是绝大多数方法都需要人工干预;二是从高亏格、拓扑复杂的网格模型中如何自动分割为高质量的粗分片的问题;三是面临不可展曲面时,如何自动生成合理的奇异点的位置以及数量,在简单参数域的前提下尽可能地保长度、保特征的参数化结果。
笔者认为,未来要结合具体领域问题的参数化目标来研究相关的离散微分几何理论(例如算子频谱以及逼近理论等),平衡好全局参数化和局部参数化方法的优缺点,才可能取得显著的突破。
3.3. 非刚性配准
3D刚性配准问题是指同一个实体在不同坐标系下采集得到的两个3D模型,经过刚体变换到同一个坐标系的同样姿态。这类算法是目标识别,误差估计算法的上游算法,具有广泛的应用意义,实现的算法也非常多。一般的分类如图2:
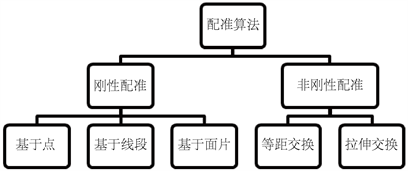
Figure 2. Classification of registration algorithms
图2. 配准算法的分类
非刚性配准问题,从微分几何角度来看是讨论所有以原点为中心,单位化的所有曲面构成的空间S中的两个微分同胚(diffeomorphism)的曲面 的映射问题。其中 经过保形的旋转变换 ,并重新参数化算子 后得到曲面 与 在某种度量 意义下的距离达到最小。即抽象为如下的优化问题:
(15)
其中的函数 是空间S中任意两个曲面之间相似度的距离。如图3所示。
是空间S中任意两个曲面之间相似度的距离。如图3所示。

Figure 3. Transitional deformation between two models measured by geodesic lines, extracted from Figure 7.2(c) in reference [1]
图3. 测地线度量下的两个模型之间的过渡变形,摘自文献 [1] 中的Figure 7.2(c)
图3中的最左侧黄色的人体曲面
从初始的经过一系列中间的曲面过渡到最左侧弯腰的人体曲面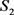 。每一个形状的参数化可以用
,
,
,
,而且
,其中
是一个向量。因此,当
时,
可视为一条连续的参数曲线
,其中
。其长度
。每一个形状的参数化可以用
,
,
,
,而且
,其中
是一个向量。因此,当
时,
可视为一条连续的参数曲线
,其中
。其长度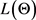 为:
为:
(16)
在(16)中的内积算子 是根据具体的空间度量来定义的,作用是测量梯度的模长。 最优化的结果是在 度量空间内找到 到 的最短路径,即测地线(Geodesic distance)。综合(15),(16),可以将非刚性配准的问题抽象为如下优化问题。
(17)
上式中包含两个优化的步骤,首先进行的优化是在S中找到从 过渡到 的测地线长度最短的路径;然后找到最优的旋转矩阵 以及参数化路径 ,使得 的各部分与 的距离尽可能靠近。
围绕上述两个优化步骤中的度量,衍生出一系列的研究。例如相似微分同胚变换、球域上的微分同胚变换以及莫比乌斯同胚变换。在文献 [34] 中,Rueckert等人研究人体器官的非刚性配准问题,提出了基于边缘熵度量体素相似度计算方法。文献 [35] 研究机械手抓取知识迁移问题,进而预测机械手的下一个运动位置,基于高斯混合模型(GMM)构建了一个非刚性配准的度量函数。文献 [36] 研究高精度导航技术中的全球导航卫星系统点云数据与移动激光扫描点云数据的非刚性配准问题,将相邻时刻采集的场景特征点集与最近点迭代算法结合,构造了刻画配准误差的能量函数,进而最小化能量函数得到预测的导航轨迹。文献 [37] 研究胎儿脑组织体积测量中的MRI成像校正问题,基于Laplacian方程提出基于颅骨切片的非刚性配准脑组织成像校正方法。另外,还有很多的研究是围绕具体领域问题中能量最小化过程中,度量函数的构造、权重来展开 [38] [39] [40] [41] [42] 。另外值得关注的是近三年来,基于各种微分算子的频谱结构的配准算法越来越受到重视 [43] [44] [45] 。
近年来的算法在处理异常数据较少、特征多的网格方面都有较好的实验结果,但对于重叠度较低或者低质量数据方面则效果不甚理想。处理噪声数据方法主要有基于RANSAC的方法、基于非参数插值的方法 [46] 以及禁忌图查找配准 [47] 等。文献 [48] 基于特征点之间的拓扑关系保持相对稳定的事实,提出了一种非刚性配准方法。
与刚性配准相比,非刚性配准面临的问题更为复杂,特别是重叠度低,弹性变形程度高的3D模型,无论何种方法,需要更多的人工干预。鉴于深度学习在人脸识别方面取得巨大的成功 [5] [49] ,笔者认为基于特定3D模型分析领域的数据训练集,将离散微分几何理论、最优传输理论 [50] [51] 与深度神经网络相结合,设计更为合理的特征最优传输算法,将可能研究出鲁棒性更好、精度更好的算法。
4. 总结
本文介绍了离散微分几何的理论框架,及其在网格去噪、网格参数化以及非刚性配准领域的应用研究现状,并对经典算法进行归纳总结。离散微分几何理论框架是基于坚实的数学理论提出来的,其中的算子是直接在离散空间上有严格的数学定义和较为成熟的数学分析方法为支撑,而不需要经历从连续空间到离散空间的转换。本文内容涵盖当前3D网格分析领域中涉及离散微分几何的一部分热点研究方向,讨论了该领域研究工作的进展和未来有待解决的问题。目前随着3D数据应用领域空前扩大,采集成本越来越低,点云的采集速度越来越快,网格数据容量也急剧膨胀,可以预见未来对这3D模型的精准、高效处理任务也会越来越有挑战性。
文章引用
吴东庆,高 健,肖正涛. 基于离散微分几何的3D网格模型分析进展综述
Review on 3D Mesh Model Analysis Based on the Discrete Differential Geometry[J]. 机械工程与技术, 2019, 08(05): 354-364. https://doi.org/10.12677/MET.2019.85041
参考文献
- 1. Xiong, L., et al. (2017) Robust Non-Rigid Registration Based on Affine ICP Algorithm and Part-Based Method. Neural Processing Letters, 48, 1305-1321. https://doi.org/10.1007/s11063-017-9760-x
- 2. Khader, M., Schiavi, E. and Hamza, A.B. (2015) A Multicomponent Approach to Nonrigid Registration of Diffusion Tensor Images. Applied Intelligence, 46, 241-253. https://doi.org/10.1007/s10489-016-0833-8
- 3. Lebedev, V.I. and Agoshkov, V.I. (2019) Poincaré-Steklov Operators and Their Applications in Analysis. Computational Processes and Systems, 2, 173-227.
- 4. Yu, W., et al. (2018) Steklov Spec-tral Geometry for Extrinsic Shape Analysis. ACM Transactions on Graphics, 38, 1-21.
- 5. Liu, J., Sun, J. and Turner, T. (2018) Spectral Indicator Method for a Non-Self Adjoint Steklov Eigenvalue Problem.
- 6. Ma, J., et al. (2017) Feature Guided Gaussian Mixture Model with Semi-Supervised EM and Local Geometric Constraint for Retinal Image Registration. Information Sciences, 417, 128-142. https://doi.org/10.1016/j.ins.2017.07.010
- 7. Laga, H., et al. (2018) 3D Shape Analysis: Fundamentals, Theory, and Applications. Wiley, Hoboken, 368. https://doi.org/10.1002/9781119405207
- 8. Adamczewski, K., Suh, Y. and Lee, K.M. (2016) Discrete Tabu Search for Graph Matching. IEEE International Conference on Computer Vision, Santiago, 7-13 December 2015, 109-117. https://doi.org/10.1109/ICCV.2015.21
- 9. Meyer, M. (2002) Discrete Differential-Geometry Operator for Triangu-lated 2-Manifolds. Visualization & Mathematics, 3, 35-57. https://doi.org/10.1007/978-3-662-05105-4_2
- 10. Ma, J., et al. (2019) Locality Preserving Matching. International Journal of Computer Vision, 127, 512-531. https://doi.org/10.1007/s11263-018-1117-z
- 11. Sun, J., Ovsjanikov, M. and Guibas, L. (2010) A Concise and Provably Informative Multi-Scale Signature Based on Heat Diffusion. Computer Graphics Forum, 28, 1383-1392. https://doi.org/10.1111/j.1467-8659.2009.01515.x
- 12. Schroff, F., Kalenichenko, D. and Philbin, J. (2015) FaceNet: A Unified Embedding for Face Recognition and Clustering. IEEE Conference on Computer Vision & Pattern Recognition, Boston, 7-12 June 2015, 815-823. https://doi.org/10.1109/CVPR.2015.7298682
- 13. Benguria, R.D., Brandolini, B. and Chiacchio, F. (2019) A Sharp Estimate for Neumann Eigenvalues of the Laplace-Beltrami Operator for Domains in a Hemisphere. Communications in Contemporary Mathematics. https://doi.org/10.1142/S0219199719500184
- 14. Peyré, G. and Cuturi, M. (2019) Computational Optimal Transport. Working Paper.
- 15. Qi, C.R., et al. (2017) PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space.
- 16. Bonneel, N. and Coeurjolly, D. (2019) SPOT: Sliced Partial Optimal Transport. ACM Transactions on Graphics, 38, Article No. 89. https://doi.org/10.1145/3306346.3323021
- 17. Wang, Y., et al. (2018) Dynamic Graph CNN for Learning on Point Clouds.
- 18. Han, Z., et al. (2017) Mesh Convolutional Restricted Boltzmann Machines for Unsupervised Learning of Fea-tures with Structure Preservation on 3-D Meshes. IEEE Transactions on Neural Networks & Learning Systems, 28, 2268-2281. https://doi.org/10.1109/TNNLS.2016.2582532
- 19. Minakshisundaram, S. and Pleijel, Å. (1949) Some Properties of the Eigenfunctions of the Laplace-Operator on Riemannian Manifolds. Canadian Journal of Mathematics, 3, 242-256. https://doi.org/10.4153/CJM-1949-021-5
- 20. Bott, R. and Tu, L.W. (2009) Differential Forms in Algebraic Topology. Graduate Texts in Mathematics Book Series (GTM, Volume 82). Springer, New York.
- 21. Desbrun, M., et al. (1999) Implicit Fairing of Irregular Meshes Using Diffusion and Curvature Flow. ACM SIGGRAPH Proceedings, Los An-geles, 28 July 2019, 317-324. https://doi.org/10.1145/311535.311576
- 22. Vaxman, A., Ben-Chen, M. and Gotsman, C. (2010) A Multi-Resolution Approach to Heat Kernels on Discrete Surfaces. ACM Transactions on Graphics, 29, 1-10. https://doi.org/10.1145/1778765.1778858
- 23. Field, D.A. (2010) Laplacian Smoothing and Delaunay Triangulations. International Journal for Numerical Methods in Biomedical Engineering, 4, 709-712. https://doi.org/10.1002/cnm.1630040603
- 24. Taubin, G. (1995) A Signal Processing Approach to Fair Surface Design. Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, 6-11 August 1995, 351-358. https://doi.org/10.1145/218380.218473
- 25. Ohtake, Y., Belyaev, A. and Bogaevski, I. (2001) Mesh Regularization and Adaptive Smoothing. Computer Aided Design, 33, 789-800. https://doi.org/10.1016/S0010-4485(01)00095-1
- 26. Yadav, S.K., Reitebuch, U. and Polthier, K. (2017) Robust and High Fidelity Mesh Denoising. IEEE Transactions on Visualization & Computer Graphics, 99, 2304-2310. https://doi.org/10.1109/TVCG.2018.2828818
- 27. Devito, Z., et al. (2017) Opt: A Domain Specific Language for Non-Linear Least Squares Optimization in Graphics and Imaging. ACM Transactions on Graphics, 36, 1-27. https://doi.org/10.1145/3132188
- 28. Taime, A., Saaidi, A. and Satori, K. (2015) Comparative Study of Mesh Simplification Algorithms. Proceedings of the Mediterranean Conference on Information & Communication Technologies, Saïdia, 7-9 May 2015, 287-295. https://doi.org/10.1007/978-3-319-30301-7_30
- 29. Dym, N., Shtengel, A. and Lipman, Y. (2015) Homotopic Morphing of Planar Curves. Computer Graphics Forum, 34, 239-251. https://doi.org/10.1111/cgf.12712
- 30. Liu, X., et al. (2010) Constrained Fairing for Meshes. Computer Graphics Fo-rum, 20, 115-123. https://doi.org/10.1111/1467-8659.00483
- 31. Zheng, Y., et al. (2011) Bilateral Normal Filtering for Mesh Denoising. IEEE Transactions on Visualization & Computer Graphics, 17, 1521-1530. https://doi.org/10.1109/TVCG.2010.264
- 32. Zhang, J., et al. (2018) Static/Dynamic Filtering for Mesh Geometry. IEEE Transactions on Visualization & Computer Graphics, 25, 1774-1787.
- 33. Yuan, G. and Sheng, Z. (2008) Monotone Finite Volume Schemes for Diffusion Equations on Polygonal Meshes. Journal of Computational Physics, 227, 6288-6312. https://doi.org/10.1016/j.jcp.2008.03.007
- 34. Seo, S., Chung, M.K. and Vorperian, H.K. (2010) Heat Kernel Smoothing Using Laplace-Beltrami Eigenfunctions. In: International Conference on Medical Image Computing & Computer-Assisted Intervention, Springer, Beijing, 505-512. https://doi.org/10.1007/978-3-642-15711-0_63
- 35. Wei, M., et al. (2019) Mesh Denoising Guided by Patch Normal Co-Filtering via Kernel Low-Rank Recovery. IEEE Transactions on Visualization and Computer Graphics, 25, 2910-2926. https://doi.org/10.1109/TVCG.2018.2865363
- 36. Tao, L., et al. (2016) Secondary Laplace Operator and Generalized Giaquinta-Hildebrandt Operator with Applications on Surface Segmentation and Smoothing. Computer-Aided Design, 70, 56-66. https://doi.org/10.1016/j.cad.2015.07.009
- 37. Alexa, M. and Wardetzky, M. (2011) Discrete Laplacians on General Polygonal Meshes. ACM Transactions on Graphics, 30, Article No. 102. https://doi.org/10.1145/2010324.1964997
- 38. Manzini, G., Russo, A. and Sukumar, N. (2014) New Perspectives on Polygonal and Polyhedral Finite Element Methods. Mathematical Models & Methods in Applied Sciences, 24, 1665-1699. https://doi.org/10.1142/S0218202514400065
- 39. Carl, W. (2016) A Laplace Operator on Semi-Discrete Surfaces. Foundations of Computational Mathematics, 16, 1115-1150. https://doi.org/10.1007/s10208-015-9271-y
- 40. 郭凤华, 张彩明, 焦文江. 网格参数化研究进展[J]. 软件学报, 2016, 27(1): 112-135.
- 41. Pinkall, U. and Polthier, K. (1993) Computing Discrete Minimal Surfaces and Their Conjugates. Experimental Mathematics, 2, 15-36. https://doi.org/10.1080/10586458.1993.10504266
- 42. Stephenson, K. (2005) Introduction to Circle Packing. Cambridge University Press, Cambridge, 12, 356.
- 43. Kharevych, L., Springborn, B. and Schröder, P. (2006) Discrete Conformal Mappings via Circle Patterns. ACM Transactions on Graphics, 25, 412-438. https://doi.org/10.1145/1138450.1138461
- 44. Gu, X.D. and Yau, S.T. (2008) Computational Conformal Geometry. Higher Education Press, Beijing, 389-429. https://doi.org/10.1007/s11786-011-0065-6
- 45. Rueckert, D. and Aljabar, P. (2015) Non-Rigid Registration Using Free-Form Deformations. In: Handbook of Biomedical Imaging: Methodologies, Springer Science + Business Media, New York, 277-294. https://doi.org/10.1007/978-0-387-09749-7_15
- 46. Rodriguez, D. and Behnke, S. (2018) Transferring Category-Based Functional Grasping Skills by Latent Space Non-Rigid Registration. IEEE Robotics & Automation Letters, 3, 2662-2669. https://doi.org/10.1109/ICRA.2018.8461169
- 47. Yan, L., et al. (2018) Automatic Non-Rigid Registration of Multi-Strip Point Clouds from Mobile Laser Scanning Systems. International Journal of Remote Sensing, 39, 1713-1728. https://doi.org/10.1080/01431161.2017.1410248
- 48. Kuklisova Murgasova, M., et al. (2017) Distortion Correction in Fetal EPI Using Non-Rigid Registration with a Laplacian Constraint. IEEE Transactions on Medical Imaging, 33, 12-19. https://doi.org/10.1109/TMI.2017.2667227
- 49. Torbati, N. and Ayatollahi, A. (2019) A Transformation Model Based on Dual-Tree Complex Wavelet Transform for Non-Rigid Registration of 3-D MRI Images. International Journal of Wavelets, Multiresolution and Information Processing, 17, Article ID: 1950025. https://doi.org/10.1142/S0219691319500255
- 50. Zhang, J., et al. (2018) Non-Rigid Image Registration by Minimizing Weighted Residual Complexity. Current Medical Imaging Reviews, 14, 334-346. https://doi.org/10.2174/1573405613666170703122534
- 51. Lai, R. and Zhao, H. (2017) Multiscale Nonrigid Point Cloud Registration Using Rotation-Invariant Sliced-Wasserstein Distance via Laplace—Beltrami Eigenmap. SIAM Journal on Imaging Sciences, 10, 449-483. https://doi.org/10.1137/16M1068827
NOTES
*通讯作者。